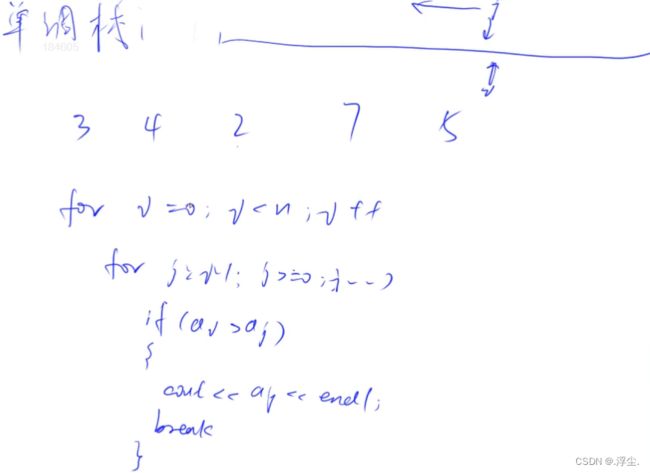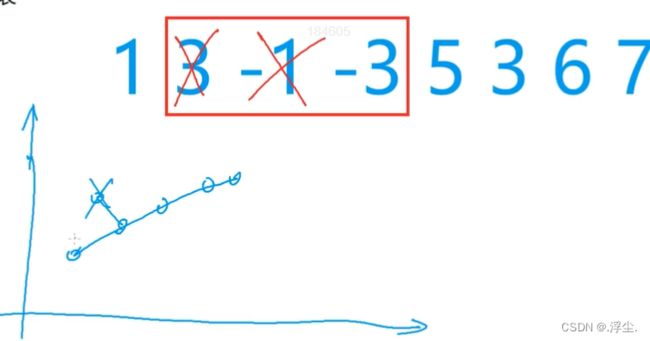数据结构（一）——链表与邻接表、栈与队列、KMP

前言

重学算法第3天，希望能坚持打卡不间断，从基础课开始直到学完提高课。
预计时长三个月内，明天再来！肝就完了

2月15日,day03 打卡
今日已学完y总的
算法基础课-2.1-第二章 数据结构（一）

共7题，知识点如下
链表与邻接表：
单链表、双链表
栈与队列：
模拟栈、模拟队列
单调栈、单调队列 ：滑动窗口（题目名）
KMP：KMP字符串

暂时先囫囵吞枣过一遍 ，以后开始大量刷题再慢慢把没完全理解的补一补

算法早学晚学都得学，不如现在直接学。
欠下的迟早要还

链表与邻接表

上述方式太慢，一般用在面试中，笔试不用

数组表示方式

单链表

模板

// head存储链表头，e[]存储节点的值，ne[]存储节点的next指针，idx表示当前用到了哪个节点
int head, e[N], ne[N], idx;

// 初始化
void init()
{
    head = -1;
    idx = 0;
}

// 在链表头插入一个数a
void insert(int a)
{
    e[idx] = a, ne[idx] = head, head = idx ++ ;
}

// 将头结点删除，需要保证头结点存在
void remove()
{
    head = ne[head];
}

AcWing 826. 单链表

思路：

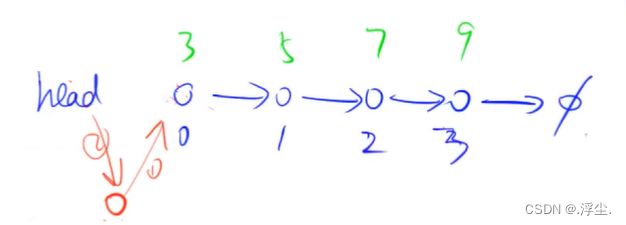
1. 将x插入到头结点

先让红色指向head里面存的这个值，再让head指向红色点

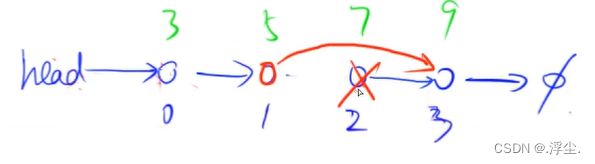
2. 将x插到下标是k的点后面

3. 将下标是k的点后面的点删掉
   

样例操作后的结果

#include 

using namespace std;

const int N = 100010;


// head 表示头结点的下标
// e[i] 表示节点i的值
// ne[i] 表示节点i的next指针是多少
// idx 存储当前已经用到了哪个点
int head, e[N], ne[N], idx;

// 初始化
void init()
{
    head = -1;
    idx = 0;
}

// 将x插入到头结点
void add_to_head(int x) { // head = idx, idx++ 可合并
    e[idx] = x, ne[idx] = head, head = idx, idx++;
}

// 将x插到下标是k的点后面
void add(int k, int x) {
    e[idx] = x, ne[idx] = ne[k], ne[k] = idx ++; 
}

// 将下标是k的点后面的点删掉
int remove(int k) {
    ne[k] = ne[ne[k]];
}

int main() {
    int m;
    cin >> m;
    
    init();
    
    while (m--) {
        int k, x;
        char op;
        
        cin >> op;
        if (op == 'H') {
            cin >> x;
            add_to_head(x);
        } else if (op == 'D') {
            cin >> k;
            if (!k) head = ne[head]; // 删除头结点,直接指向下一个点
            remove(k - 1); // 第k个点,下标k-1
        } else {
            cin >> k >> x;
            add(k - 1, x);
        }
    }
    
    for (int i = head; i != - 1; i = ne[i]) // i从头结点开始,没遍历到空节点,每次i往后走一步
        cout << e[i] << ' '; // 输出i对应的值
    cout << endl;
    
    return 0;
}

算法题不需要考虑内存泄露的问题，做项目才需要

双链表

模板

// e[]表示节点的值，l[]表示节点的左指针，r[]表示节点的右指针，idx表示当前用到了哪个节点
int e[N], l[N], r[N], idx;

// 初始化
void init()
{
    //0是左端点，1是右端点
    r[0] = 1, l[1] = 0;
    idx = 2;
}

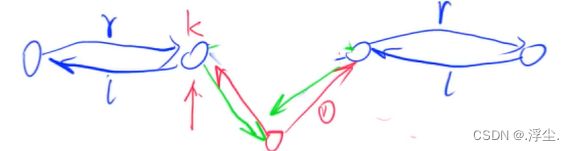
// 在节点a的右边插入一个数x
void insert(int a, int x)
{
    e[idx] = x;
    l[idx] = a, r[idx] = r[a];
    l[r[a]] = idx, r[a] = idx ++ ;
}

// 删除节点a
void remove(int a)
{
    l[r[a]] = l[a];
    r[l[a]] = r[a];
}

AcWing 827. 双链表

思路：

1. 初始化
   

2. 在节点k的右边插入一个数x
   

3. 删除
   

#include 

using namespace std;

const int N = 100010;

int m;
int e[N], l[N], r[N], idx;

//初始化
void init() {
    // 0 表示左端点,1表示右端点
    r[0] = 1, l[1] = 0; // 0号点的右边是1,1号点的左边是0
    idx = 2; // 0和1被占用了
}

// 在节点k的右边插入一个数x
void insert(int k, int x) {
    e[idx] = x;
    r[idx] = r[k];
    l[idx] = k;  
    l[r[k]] = idx; // 需要先改原来r[k]左指针的值,因为下面r[k]要指向idx
    r[k] = idx ++; // idx需要++
}

// 删除第k个点
void remove(int k) {
    r[l[k]] = r[k]; // k的左边点的右节点指向k的右边点
    l[r[k]] = l[k]; // k的右边点的左节点指向k的左边点
}


int main()
{
    cin >> m;
    
    init();
    
    while (m -- )
    {
        string op;
        cin >> op;
        int k, x;
        if (op == "L")
        {
            cin >> x;
            insert(0, x);
        }
        else if (op == "R")
        {
            cin >> x;
            insert(l[1], x);
        }
        else if (op == "D")
        {
            cin >> k;
            remove(k + 1);
        }
        else if (op == "IL")
        {
            cin >> k >> x;
            insert(l[k + 1], x);
        }
        else
        {
            cin >> k >> x;
            insert(k + 1, x);
        }
    }

    for (int i = r[0]; i != 1; i = r[i]) cout << e[i] << ' ';
    cout << endl;

    return 0;
}

栈与队列

栈：先入后出
队列：先入先出

模板需要锻炼熟练度，多背多写（要理解+熟练）
记忆力 +　毅力（自制力）

栈和队列的操作

#include 

using namespace std;

const int N = 100010;

// ************************ 栈
int stk[N] tt; // 初始为0
// 插入
stk[++ tt] = x;
// 弹出
tt--;

// 判断栈是否为空
if (tt > 0) not empty
else empty

// 栈顶
stk[tt]

// ************************ 队列

// 在队尾插入元素，在队头弹出元素,hh队头,tt队尾
int q[N], hh, tt = -1; // 队列从-1开始,看个人习惯,都行

// 插入
q[++ tt] = x;

// 弹出
hh++;

if (hh <= tt)

// 判断队列是否为空
if (hh > tt) not empty
else empty

// 取出队头元素
q[hh]

模拟栈

模板

// tt表示栈顶
int stk[N], tt = 0;

// 向栈顶插入一个数
stk[ ++ tt] = x;

// 从栈顶弹出一个数
tt -- ;

// 栈顶的值
stk[tt];

// 判断栈是否为空
if (tt > 0)
{

}

AcWing 828. 模拟栈

思路：相出对应操作怎么处理直接写就行了

#include 

using namespace std;

const int N = 100010;

int m;
int stk[N], tt;

int main() {
    cin >> m;
    while (m --) {
        string op;
        int x;
        cin >> op;
        if (op == "push") {
            cin >> x;
            stk[++ tt] = x;
        } 
        else if (op == "pop") tt--;
        else if (op == "empty") cout << (tt ? "NO" : "YES") << endl;
        else cout << stk[tt] << endl;
    }
    
    return 0;
}

模拟队列

模板

// hh 表示队头，tt表示队尾
int q[N], hh = 0, tt = -1;

// 向队尾插入一个数
q[ ++ tt] = x;

// 从队头弹出一个数
hh ++ ;

// 队头的值
q[hh];

// 判断队列是否为空
if (hh <= tt)
{

}

AcWing 829. 模拟队列

#include 

using namespace std;

const int N = 100010;

int m;
// 在队尾插入元素，在队头弹出元素,hh队头,tt队尾
int q[N], hh, tt = -1;

int main() {
    cin >> m;
    
    while (m --) {
        string op;
        int x;
        cin >> op;
        
        if (op == "push") {
            cin >> x;
            q[++ tt] = x;
        } 
        else if (op == "pop") hh ++;
        else if (op == "empty") cout << (hh <= tt ? "NO" : "YES") << endl;
        else cout << q[hh] << endl;
    }
    
    return 0;
}

单调栈

模板

常见模型：找出每个数左边离它最近的比它大/小的数
int tt = 0;
for (int i = 1; i <= n; i ++ )
{
    while (tt && check(stk[tt], i)) tt -- ;
    stk[ ++ tt] = i;
}

AcWing 830. 单调栈

思路：

暴力做法：找出ｉ的左边比ｉ小的第一个数

找性质

将所有离i更远且有比它大的值都删掉，如图，1和2位置对应的点
stk1] > stk[2]，且离i更远，删掉stk[1]
删掉所有这样的点，会得到一个单调递增序列

然后将stk[tt](栈顶)所有比 i 所在值大的数都删掉(a[i])
直到slt[tt] < a[i] 就找到了

#include 

using namespace std;

const int N = 100010;

int n;
int stk[N], tt;
// 使用scanf和printf速度能加快许多，输出输出较大的话，推荐使用
// cin 984 ms
// scanf 	113 ms
int main () {
    //cin >> n;
    scanf ("%d", &n);
    
    for (int i = 0; i < n; i++) {
        int x;
        //cin >> x;
        scanf ("%d", &x);
        
        while (tt && stk[tt] >= x)  tt--; // 将stk[tt](栈顶)所有比 a[i]大的数都删掉
        if (tt) 
            //cout << stk[tt] << ' ';
            printf("%d ", stk[tt]);
        else 
            //cout << -1 << ' ';
            printf("-1 ");
        stk[++ tt] = x; // 将x插入栈内
    }
    
    return 0;
}

时间复杂度是O(n)
虽然看着有两重循环，但每个数只会进栈一次，最多出栈一次，只有2N次操作，所以是O(n)

单调队列

模板

常见模型：找出滑动窗口中的最大值/最小值
int hh = 0, tt = -1;
for (int i = 0; i < n; i ++ )
{
    while (hh <= tt && check_out(q[hh])) hh ++ ;  // 判断队头是否滑出窗口
    while (hh <= tt && check(q[tt], i)) tt -- ;
    q[ ++ tt] = i;
}

AcWing 154. 滑动窗口

思路：

暴力是O（nk）
第一步：插入新元素
第二步：将划出去的从队尾弹出

依然是将逆序的全部删掉，形成单调递增序列

最小值就是最左边的点，q[h][h] （队头）
最大值是一样的操作

怎么知道队首元素如何出列？

该题中 i 是最右值下标，k 是窗口范围
q[] 中存的是下标
所以可以判断q[hh] 是否超出了 [i - k + 1，i] 的范围
超出就把队头删掉

#include 

using namespace std;

const int N = 1000010;

int n, k;
int a[N], q[N]; // q[]中存的是下标

int main() {
    scanf("%d%d", &n, &k);
    for (int i = 0; i < n; i ++) scanf("%d", &a[i]);
    
    int hh = 0, tt = -1;
    for (int i = 0; i < n; i++) {
        // 判断队头是否已经划出窗口
        if (hh <= tt && i -k + 1 > q[hh]) hh++;  // 每次最多只有一个数不在窗口内,所以可以用if
        // 新插入的数比队尾小就把队尾删掉-->单调递增
        while (hh <= tt && a[q[tt]] >= a[i])  tt--;  
        q[++ tt] = i; // 将当前数插入队列 i也可能是最小值
        // 判断一下,有k个数才开始输出
        if (i >= k - 1) printf("%d ", a[q[hh]]);
    }
    puts(""); // 输出回车
    
    // 最大值是完全对称的写法
    hh = 0, tt = -1;
    for (int i = 0; i < n; i++) {
        // 判断队头是否已经划出窗口
        if (hh <= tt && i -k + 1 > q[hh]) hh++;  
        // 新插入的数比队尾大就把队尾删掉-->单调递减
        while (hh <= tt && a[q[tt]] <= a[i])  tt--;  
        q[++ tt] = i; 

        if (i >= k - 1) printf("%d ", a[q[hh]]);
    }
    puts("");
    
    return 0;
} 

思路总结：

先考虑暴力怎么做，再考虑把没用的元素删掉，再看有没有单调性，有就可以做优化。
取极值可以选左右两端点，找一个值可以用二分

KMP

朴素做法

kmp中next数组的含义
对于某个点的
后缀 和 前缀 相等的长度最大是多少
红色线最少移动多少能继续匹配

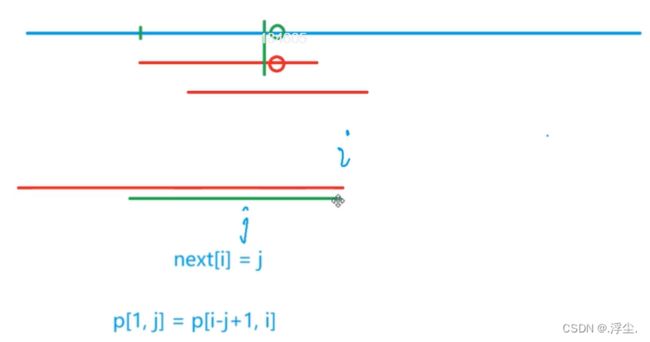
前后缀相等长度，所以下面是next[j]
next[j]再与s[i]比看是否匹配，如果不匹配就接着找下一个next[j]

找next，看下一个是否匹配

模板

// s[]是长文本，p[]是模式串，n是s的长度，m是p的长度
求模式串的Next数组：
for (int i = 2, j = 0; i <= m; i ++ )
{
    while (j && p[i] != p[j + 1]) j = ne[j];
    if (p[i] == p[j + 1]) j ++ ;
    ne[i] = j;
}

// 匹配
for (int i = 1, j = 0; i <= n; i ++ )
{
    while (j && s[i] != p[j + 1]) j = ne[j];
    if (s[i] == p[j + 1]) j ++ ;
    if (j == m)
    {
        j = ne[j];
        // 匹配成功后的逻辑
    }
}

AcWing 831. KMP字符串

例子

next[] 是前后缀相等的 最大长度
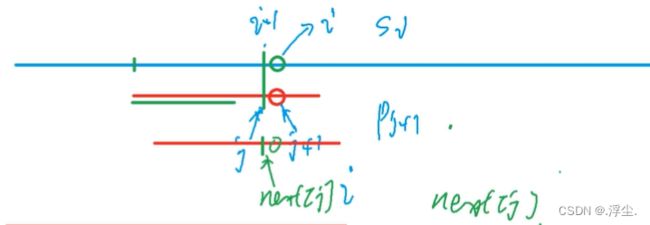
当p[j+1] 与 S[i] 不想等
就将j指到next[j]处，
如图 ，j 此时 为next[6] = 4
因为是前后缀相同的最大长度，所以此时与原来的后半段值是相等的
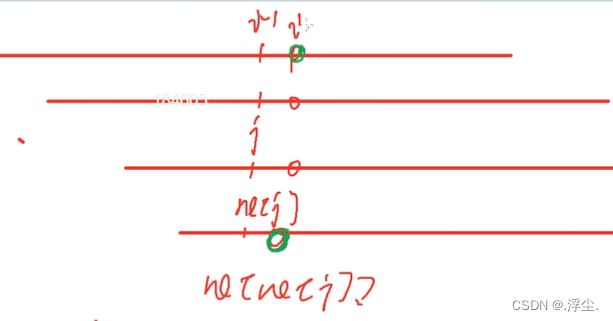
不匹配的话接着往前跳，直到比完

#include 

using namespace std;

const int N = 10010, M = 100010;

int n, m;
char p[N], s[M];
int ne[N]; // next在C++中可能报错,某个头文件中用过

int main() {
    cin >> n >> p + 1 >> m >> s + 1; // 下标从1开始
    
    // 求next的过程
    for (int i = 2, j = 0; i <= n; i++) {
        while (j && p[i] != p[j + 1]) j = ne[j];
        if (p[i] == p[j + 1]) j++; // 相等就前进一步
        ne[i] = j;
    }
    
    // kmp匹配过程
    for (int i = 1, j = 0; i <= m; i++) { // 和s[i]匹配的是p[j+1]
        // 不匹配了退一步,看什么时候能接着走,如果还是不能匹配就直接看下一个位置
        while (j && s[i] != p[j + 1]) j = ne[j];
        if (s[i] == p[j+1]) j++; //如果已经匹配就将j移到下一个位置
        if (j == n) {
            // 匹配成功
            printf("%d ", i - n); // 题目下标从0开始,所以需要减一(i-n+1-1)
            j = ne[j]; // 匹配成功后看下一个是能否匹配需要移动的最短距离next[j]
        }
    }
    
    return 0;
}

暂时不管了，以后遇到了kmp再补补

也不指望能一遍把所有算法学会，先过一遍，留个印象和笔记，以后遇到了再补对应的就好了