无线物理层安全大作业
这个标题很帅
- Beamforming Optimization for Physical Layer Security in MISO Wireless Networks
- Problem Stateme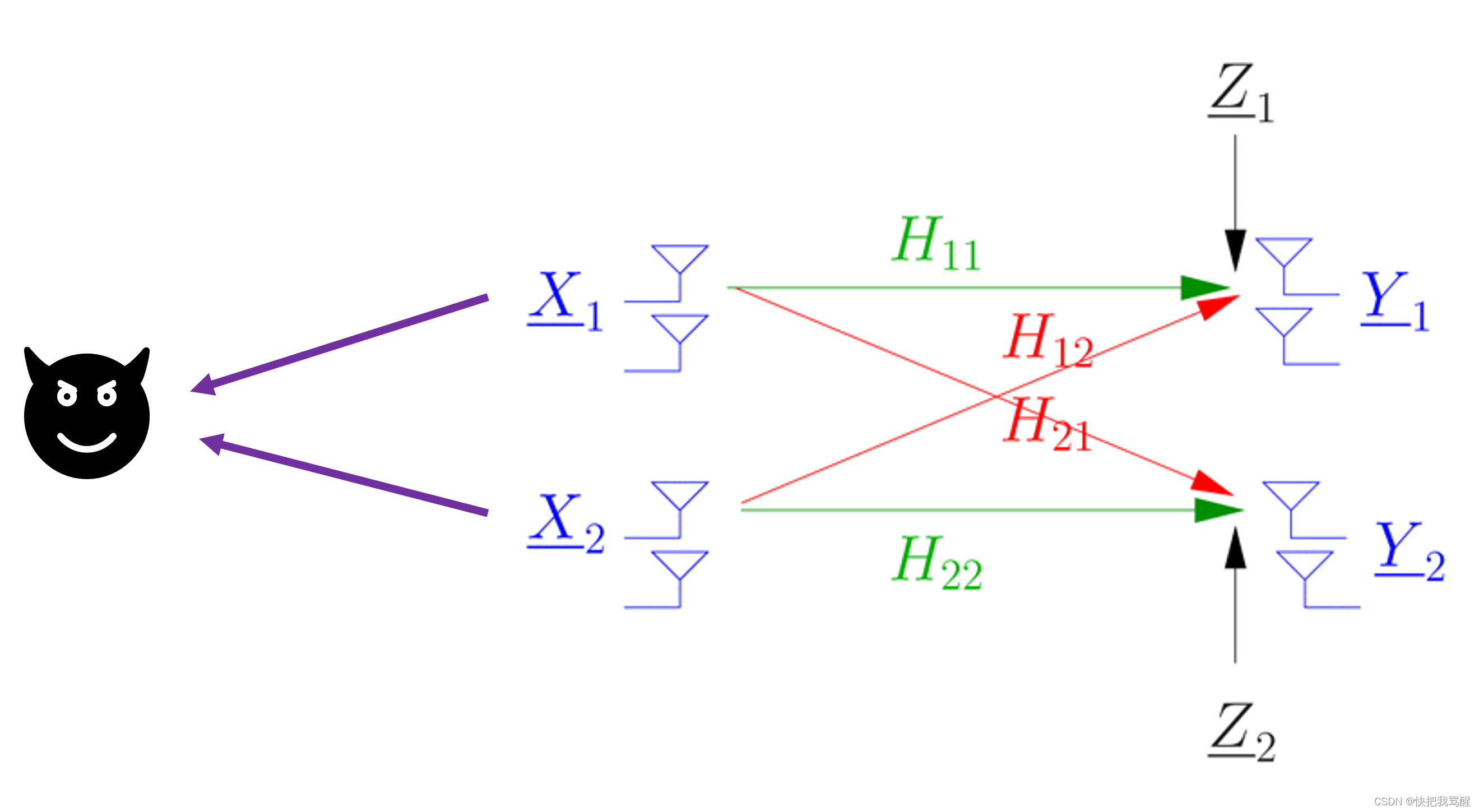
- INSTANTANEOUS SECRECY THROUGHPUT OPTIMIZATION
-
- 算法1
- 算法2
- EV’S OUTAGE PROBABILITY MAXIMIZATION
-
- 推导 
- 算法3
- ROBUST OPTIMIZATION TO COMPENSATE USERS’ OUTAGE PROBABILITY
-
- 算法4
- 结论
- 有关附录
-
- 附录一
- 附录二
- 附录 III
Beamforming Optimization for Physical Layer Security in MISO Wireless Networks
2018 TSP
考虑由窃听者窃听的多个发射机-用户对组成的无线网络,其中发射机配备有多个天线,而用户和窃听者配备有单个天线。在不同级别的无线信道知识中,感兴趣的问题是波束成形,以根据用户的保密吞吐量优化用户的服务质量(QoS),或在用户的 QoS 下最大化网络的能源效率。所有这些问题都被视为非常困难的优化问题,在波束成形向量中具有许多非凸约束和非线性等式约束。本文开发了低复杂度和快速收敛的路径跟踪计算程序,以获得最佳波束形成解决方案。通过数值例子证明了它们的实用性。
保护信息已成为无线通信中最关键的问题之一[1]、[2]。无线传输的广播性质意味着它们很容易受到对手的攻击,对手试图拦截其信息传递或无意中听到为其用户提供的机密信息[3]、[4]。已经提出利用无线信道[5]、[6]的物理特性的物理层安全性(PLS)来确保向低复杂性的最终用户传输数据的保密性,对此不能使用加密。 PLS 基于保密的信息论特征,窃听者 (EV) 监听到的无线传输的用户保密吞吐量被确定为用户吞吐量与 EV 吞吐量之间的差值 [2]、[7]。传输波束成形可提高用户吞吐量,同时控制 EV 处窃听信号的吞吐量,从而提供了一种增强保密吞吐量的有效方法。 [8]-[12] 中已经考虑通过半定松弛和随机化以及已知的低效率 [13] 来最大化瞬时保密吞吐量的波束成形设计。这种波束成形设计已在[14]、[15]中成功解决。关于中断概率,[16]-[19]等一些著作使用了未发表的著作[20]中获得的伯恩斯坦型不等式。我们将证明,基于这种伯恩斯坦型不等式的结果可能非常保守。参考文献[21]考虑了在不完美信道状态信息(CSI)下给定波束形成器的中断区域特征。
另一方面,随着能源效率(EE)成为无线通信中非常严重的问题[22]、[23],安全能源效率(SEE),即保密吞吐量与总网络功耗的比率,以每焦耳每赫兹的保密位数来衡量在 PLS 中也越来越重要 [24]、[25]。利用完美的CSI,[26]-[28]中的SEE最大化基于昂贵的波束形成器,它完全消除了EV上的多用户干扰和窃听信号。 [29]和[30]中单用户多输入多输出(MIMO)/单输入单输出(SISO)通信的SEE优化算法的计算复杂度也很高,因为每次迭代仍然涉及困难非凸优化问题。我们之前的工作 [31] 考虑了更一般的 MIMO 网络情况的 SEE 优化。 [15] 中还考虑了 SEE 优化,以应对用户和电动汽车渠道不确定性的最坏情况。目前还没有关于在中断概率方面具有保密吞吐量的 SEE 优化的现有工作。
在本文中,我们考虑由窃听者 (EV) 窃听的多个发射器用户对组成的网络。由于假设发射机配备多个天线,而用户和 EV 配备单个天线,因此目标是设计发射波束形成器,以在保密吞吐量方面优化用户的服务质量 (QoS)或用户QoS下网络的SEE。应该意识到,波束成形设计的这些问题仍然有广泛的研究空间,因此我们在不同的信道知识层面上考虑它们。本文的结构如下。第二节专门讨论问题陈述。第三部分考虑了所有相关通道的完美 CSI 下的这些问题,其中开发了低复杂度的路径跟踪算法来解决这些问题。在第四节中,假设发射机和用户之间的信道的完美CSI,但仅假设发射机和EV之间的信道分布是已知的。因此,EV 的吞吐量不是确定性定义的,而是通过其中断概率来定义的,这导致波束成形向量和 EV 吞吐量中的非线性方程,使得波束成形设计在计算上更具挑战性。在与第四节中发射机和EV之间的信道相同的知识下,第五节还假设发射机和用户之间的信道是不确定的,具有高斯分布误差,在这种情况下,用户的中断概率没有已知的结果。吞吐量。尽管如此,基于附录一中获得的新的中断概率结果,用户的QoS优化和网络的SEE优化问题都得到了成功的解决。第五节的仿真显示了第三节至第五节中开发的路径跟踪算法的效率。第六节给出了结论。附录一提供了有关中断感知用户吞吐量上限和下限的新结果。附录二显示了其他一些结果的保守性,这些结果基于伯恩斯坦型不等式。附录 III 中给出了第 III-V 节中使用的一些基本确定性不等式。
Problem Stateme
考虑由 EV 监听的 M 个发射机-用户对的通信网络。每个发射机配备Nt个发射天线,而用户和EV配备单个天线。因此,在没有 EV 的情况下,网络看起来非常类似于[32]-[36]中考虑的网络,其中信道知识是从信道估计中获得的,信道估计在网络的中央处理单元中实现,而波束成形在网络的信号处理块。用户 i i i 的信息 s i s_i si 被归一化为 E ( s i 2 ) = 1 E(s^2_i )=1 E(si2)=1,通过 w i ∈ C N t \mathbf{w}_i \in \mathbb{C}^{N_t} wi∈CNt 进行波束形成。用户 i i i处接收到的信号为
y i = h i i H w i s i + ∑ j ≠ i M h j i H w j s j + n i (1) y_{i}=h_{i i}^{H} \mathbf{w}_{i} s_{i}+\sum_{j \neq i}^{M} h_{j i}^{H} \mathbf{w}_{j} s_{j}+n_{i} \tag{1} yi=hiiHwisi+j=i∑MhjiHwjsj+ni(1)
INSTANTANEOUS SECRECY THROUGHPUT OPTIMIZATION
算法1
基本就是MM算法找上界然后不断迭代

max w Φ ( κ ) ( w ) ≜ min i = 1 , … , M [ f i ( κ ) ( w ) − g i ( κ ) ( w ) ] s.t. ( 3 b ) , ( 9 ) , ( 12 ) . (13) \begin{align} \max _{\boldsymbol{w}} \Phi^{(\kappa)}(\mathbf{w}) \triangleq \min _{i=1, \ldots, M}\left[f_{i}^{(\kappa)}(\boldsymbol{w})-g_{i}^{(\kappa)}(\boldsymbol{w})\right] \\ \text { s.t. } \quad(3 b),(9),(12) . \end{align} \tag{13} wmaxΦ(κ)(w)≜i=1,…,Mmin[fi(κ)(w)−gi(κ)(w)] s.t. (3b),(9),(12).(13)
Secrecy throughput maximin optimization under transmitters’ power constraints:
max w Φ ( w ) ≜ min i = 1 , … , M [ f i ( w ) − g i ( w ) ] s.t. ∥ w i ∥ 2 ≤ P i , i = 1 , … , M \begin{align} \max _{\mathbf{w}} \Phi(\mathbf{w}) \triangleq \min _{i=1, \ldots, M}\left[f_{i}(\mathbf{w})-g_{i}(\mathbf{w})\right] \quad \text { s.t. } \tag{3a}\\ \left\|\mathbf{w}_{i}\right\|^{2} \leq P_{i}, i=1, \ldots, M \tag{3b} \end{align} wmaxΦ(w)≜i=1,…,Mmin[fi(w)−gi(w)] s.t. ∥wi∥2≤Pi,i=1,…,M(3a)(3b)
可行域
2 ℜ { ( w i ( κ ) ) H h i i h i i H w i } − ∣ h i i H w i ( κ ) ∣ 2 > 0 i = 1 , … , M (9) \begin{array}{r} 2 \Re\left\{\left(w_{i}^{(\kappa)}\right)^{H} h_{i i} h_{i i}^{H} \mathbf{w}_{i}\right\}-\left|h_{i i}^{H} w_{i}^{(\kappa)}\right|^{2}>0 \\ i=1, \ldots, M \end{array} \tag{9} 2ℜ{(wi(κ))HhiihiiHwi}− hiiHwi(κ) 2>0i=1,…,M(9)
x i ( κ ) = ∣ h i i H w i ( κ ) ∣ 2 ∑ j ≠ i M ∣ h j i H w j ( κ ) ∣ 2 + σ i 2 . x_{i}^{(\kappa)}=\frac{\left|h_{i i}^{H} w_{i}^{(\kappa)}\right|^{2}}{\sum_{j \neq i}^{M}\left|h_{j i}^{H} w_{j}^{(\kappa)}\right|^{2}+\sigma_{i}^{2}} . xi(κ)=∑j=iM hjiHwj(κ) 2+σi2 hiiHwi(κ) 2.
∑ j ≠ i M ( 2 ℜ { ( w j ( κ ) ) H h j e h j e H w j } − ∣ h j e H w j ( κ ) ∣ 2 ) > 0 i = 1 , … , M (12) \begin{array}{r} \sum_{j \neq i}^{M}\left(2 \Re\left\{\left(w_{j}^{(\kappa)}\right)^{H} h_{j e} h_{j e}^{H} \mathbf{w}_{j}\right\}-\left|h_{j e}^{H} w_{j}^{(\kappa)}\right|^{2}\right)>0 \\ i=1, \ldots, M \end{array} \tag{12} ∑j=iM(2ℜ{(wj(κ))HhjehjeHwj}− hjeHwj(κ) 2)>0i=1,…,M(12)
算法2
对能量效率也是找了个下界
max w ∑ i = 1 M [ f i ( κ ) ( w ) − g i ( κ ) ( w ) ] − Θ ( w ( κ ) ) π ( w ) s.t. ( 3 b ) , ( 9 ) , ( 12 ) , f i ( κ ) ( w ) − g i ( κ ) ( w ) ≥ c i , i = 1 , … , M . (15) \begin{array}{r} \max _{\boldsymbol{w}} \sum_{i=1}^{M}\left[f_{i}^{(\kappa)}(\boldsymbol{w})-g_{i}^{(\kappa)}(\boldsymbol{w})\right]-\Theta\left(w^{(\kappa)}\right) \pi(\mathbf{w}) \\ \text { s.t. } \quad(3 b),(9),(12), \\ f_{i}^{(\kappa)}(\boldsymbol{w})-g_{i}^{(\kappa)}(\boldsymbol{w}) \geq c_{i}, i=1, \ldots, M . \end{array} \tag{15} maxw∑i=1M[fi(κ)(w)−gi(κ)(w)]−Θ(w(κ))π(w) s.t. (3b),(9),(12),fi(κ)(w)−gi(κ)(w)≥ci,i=1,…,M.(15)
EV’S OUTAGE PROBABILITY MAXIMIZATION
推导 
第一步的时候引用的[38]
Z. Sheng, H. D. Tuan, A. A. Nasir, T. Q. Duong, and H. V. Poor, “Power
allocation for energy efficiency and secrecy of wireless interference net-
works,” IEEE Trans. Wireless Commun., no. 99, pp. 1–1, 2018.
文章[38]的主要内容:
考虑带有窃听者的多用户干扰网络,本文旨在优化网络链路间最差保密吞吐量的功率分配,或者在链路安全要求下,以每焦耳达到的保密吞吐量表示的安全能量效率。考虑信道状态信息访问的三种情况:完美的信道状态信息;从发射机到窃听者的信道呈指数分布的部分信道状态信息;以及发射机和用户之间具有指数分布误差的不完全已知的信道。本文发展了各种低复杂度和快速收敛的路径跟踪过程,用于最优功率分配。数值例子说明了它们的有效性和可行性。功率分配方案被证明实现了高保密吞吐量和能量效率。
当 EV 不是合法网络的一部分时,几乎不可能估计从发射机到它的信道。通常假设 hie=´hieχie,其中 χie 是具有单位均值的指数分布,而 ´hie 是已知的确定性量。因此,EV 上用户 i 的窃听吞吐量不是 (2),而是通过以下吞吐量中断定义 [29]-[33]:
g i , o ( p ) ≜ max { ln ( 1 + r i ) : Prob ( h i e p i ∑ j ≠ i h j e p j + σ e 2 < r i ) ≤ ϵ E V } (25) \begin{aligned} g_{i, o}(\mathbf{p}) \triangleq \max & \left\{\ln \left(1+\mathbf{r}_{i}\right):\right. \\ & \left.\operatorname{Prob}\left(\frac{h_{i e} \mathbf{p}_{i}}{\sum_{j \neq i} h_{j e} \mathbf{p}_{j}+\sigma_{e}^{2}}<\mathbf{r}_{i}\right) \leq \epsilon_{E V}\right\} \tag{25} \end{aligned} gi,o(p)≜max{ln(1+ri):Prob(∑j=ihjepj+σe2hiepi<ri)≤ϵEV}(25)
for ϵ E V > 0 \epsilon_{E V} > 0 ϵEV>0. Using (63) in Appendix I, it follows that
ln ( 1 − ε ) + r σ 2 p 1 λ ˉ 1 + ∑ i = 2 n ln ( 1 + r p i λ ˉ i p 1 λ ˉ 1 ) = 0 \ln (1-\varepsilon)+\frac{r \sigma^{2}}{p_{1} \bar{\lambda}_{1}}+\sum_{i=2}^{n} \ln \left(1+\frac{r p_{i} \bar{\lambda}_{i}}{p_{1} \bar{\lambda}_{1}}\right)=0 ln(1−ε)+p1λˉ1rσ2+i=2∑nln(1+p1λˉ1rpiλˉi)=0
[38]的Prop.1
算法3
仅知道窃听信道的分布
窃听信道服从高斯分布
高斯分布的模方是指数分布
窃听者的中断概率最大化

max w , r min i = 1 , … , M [ ln ( 1 + ∣ h i i H w i ∣ 2 ∑ j ≠ i ∣ h j i H w j ∣ 2 + σ i 2 ) − ln ( 1 + r i ) ] s.t ( 3 b ) , g i , o ( w , r i ) ≥ 0 , i = 1 , … , M , r i > 0 , \begin{align} \max _{\boldsymbol{w}, \mathbf{r}} \min _{i=1, \ldots, M}\left[\ln \left(1+\frac{\left|h_{i i}^{H} \mathbf{w}_{i}\right|^{2}}{\sum_{j \neq i}\left|h_{j i}^{H} \mathbf{w}_{j}\right|^{2}+\sigma_{i}^{2}}\right)\right. \notag \\ \left.-\ln \left(1+\mathbf{r}_{i}\right)\right] \text { s.t } \quad(3 b), \tag{21a}\\ g_{i, o}\left(\mathbf{w}, \mathbf{r}_{i}\right) \geq 0, i=1, \ldots, M, \tag{21b}\\ \mathbf{r}_{i}>0, \tag{21c} \end{align} w,rmaxi=1,…,Mmin[ln(1+∑j=i hjiHwj 2+σi2 hiiHwi 2)−ln(1+ri)] s.t (3b),gi,o(w,ri)≥0,i=1,…,M,ri>0,(21a)(21b)(21c)
max w , r min i = 1 , … , M [ f i ( κ ) ( w ) − a i ( κ ) ( r i ) ] s.t ( 3 b ) , ( 9 ) , ( 21 c ) , ( 23 ) , g i , o ( κ ) ( w , r i ) ≥ 0 , i = 1 , … , M . \begin{align} \max _{\boldsymbol{w}, \mathbf{r}} \min _{i=1, \ldots, M}\left[f_{i}^{(\kappa)}(\mathbf{w})-a_{i}^{(\kappa)}\left(\mathbf{r}_{i}\right)\right] \notag \\ \text { s.t } \quad(3 b),(9),(21 c),(23), \tag{30a}\\ g_{i, o}^{(\kappa)}\left(\mathbf{w}, \mathbf{r}_{i}\right) \geq 0, i=1, \ldots, M . \tag{30b} \end{align} w,rmaxi=1,…,Mmin[fi(κ)(w)−ai(κ)(ri)] s.t (3b),(9),(21c),(23),gi,o(κ)(w,ri)≥0,i=1,…,M.(30a)(30b)
2 ℜ { ( w j ( κ ) ) H w j } − ∥ w j ( κ ) ∥ 2 > 0 (23) 2 \Re\left\{\left(w_{j}^{(\kappa)}\right)^{H} \mathbf{w}_{j}\right\}-\left\|w_{j}^{(\kappa)}\right\|^{2}>0 \tag{23} 2ℜ{(wj(κ))Hwj}− wj(κ) 2>0(23)
ψ i ( r i ) ≜ g i , o ( w ( κ ) , r i ) = 0 , i = 1 , … , M (31) \psi_{i}\left(\mathbf{r}_{i}\right) \triangleq g_{i, o}\left(w^{(\kappa)}, \mathbf{r}_{i}\right)=0, \quad i=1, \ldots, M \tag{31} ψi(ri)≜gi,o(w(κ),ri)=0,i=1,…,M(31)
用二分搜索去解
ROBUST OPTIMIZATION TO COMPENSATE USERS’ OUTAGE PROBABILITY
算法4
Robust优化即不完美的CSI下的优化

max w , R , r min i = 1 , … , M [ ln ( 1 + R i ) − ln ( 1 + r i ) ] s.t ( 3 b ) , ( 21 b ) , ( 21 c ) , φ i ( w , R i ) > 0 , i = 1 , … , M , δ [ δ M ∥ w min ∥ 2 + M − 1 2 ∥ w min ∥ 2 ln φ i ( w , R i ) ∥ w min ∥ 2 ] ≤ φ i ( w , R i ) , i = 1 , … , M , \begin{align} \max _{\boldsymbol{w}, \mathbf{R}, \mathbf{r}} \min _{i=1, \ldots, M}\left[\ln \left(1+\mathbf{R}_{i}\right)-\ln \left(1+\mathbf{r}_{i}\right)\right] \notag \\ \text { s.t }(3 b),(21 b),(21 c), \tag{40a} \\ \varphi_{i}\left(\mathbf{w}, \mathbf{R}_{i}\right)>0, i=1, \ldots, M, \tag{40b} \\ \delta\left[\delta_{M}\left\|\mathbf{w}_{\text {min }}\right\|^{2}+\frac{M-1}{2}\left\|\mathbf{w}_{\text {min }}\right\|^{2} \ln \frac{\varphi_{i}\left(\mathbf{w}, \mathbf{R}_{i}\right)}{\left\|\mathbf{w}_{\text {min }}\right\|^{2}}\right] \notag \\ \leq \varphi_{i}\left(\mathbf{w}, \mathbf{R}_{i}\right), i=1, \ldots, M, \tag{40c} \end{align} w,R,rmaxi=1,…,Mmin[ln(1+Ri)−ln(1+ri)] s.t (3b),(21b),(21c),φi(w,Ri)>0,i=1,…,M,δ[δM∥wmin ∥2+2M−1∥wmin ∥2ln∥wmin ∥2φi(w,Ri)]≤φi(w,Ri),i=1,…,M,(40a)(40b)(40c)
max w , R , r min i = 1 , … , M [ A i ( κ ) ( R i ) − a i ( κ ) ( r i ) ] s.t ( 3 b ) , ( 21 c ) , ( 23 ) , ( 30 b ) , ( 41 ) , ( 44 ) . \begin{align} \max _{\boldsymbol{w}, \mathbf{R}, \mathbf{r}} \min _{i=1, \ldots, M}\left[A_{i}^{(\kappa)}\left(\mathbf{R}_{i}\right)-a_{i}^{(\kappa)}\left(\mathbf{r}_{i}\right)\right] \notag\\ \text { s.t } \quad(3 b),(21 c),(23),(30 b),(41),(44) . \tag{45} \end{align} w,R,rmaxi=1,…,Mmin[Ai(κ)(Ri)−ai(κ)(ri)] s.t (3b),(21c),(23),(30b),(41),(44).(45)
ℓ i ( κ ) ( w i , R i ) > ( 1 − δ ) − 1 ∑ j ≠ i M ∣ h ˉ j i H w j ∣ 2 + σ i 2 , i = 1 , … , M \begin{align} \ell_{i}^{(\kappa)}\left(\mathbf{w}_{i}, \mathbf{R}_{i}\right)>(1-\delta)^{-1} \sum_{j \neq i}^{M}\left|\bar{h}_{j i}^{H} \mathbf{w}_{j}\right|^{2}+\sigma_{i}^{2}, \notag \\ i=1, \ldots, M \tag{41} \end{align} ℓi(κ)(wi,Ri)>(1−δ)−1j=i∑M hˉjiHwj 2+σi2,i=1,…,M(41)
δ [ M − 1 2 ( ln ( x i ( κ ) ) − 1 ) + δ M ] ∥ w i m i n ∥ 2 ≤ ( 1 − δ ( M − 1 ) / 2 x i ( κ ) ) φ i ( κ ) ( w , R i ) i = 1 , … , M . (44) \begin{array}{r} \delta\left[\frac{M-1}{2}\left(\ln \left(x_{i}^{(\kappa)}\right)-1\right)+\delta_{M}\right]\left\|\mathbf{w}_{i_{\mathrm{min}}}\right\|^{2} \\ \leq\left(1-\delta(M-1) / 2 x_{i}^{(\kappa)}\right) \varphi_{i}^{(\kappa)}\left(\mathbf{w}, \mathbf{R}_{i}\right) \\ i=1, \ldots, M . \end{array} \tag{44} δ[2M−1(ln(xi(κ))−1)+δM]∥wimin∥2≤(1−δ(M−1)/2xi(κ))φi(κ)(w,Ri)i=1,…,M.(44)
结论
对于窃听者偷听的多个发射机-用户对的无线网络,我们考虑了波束成形设计,以在用户保密吞吐量阈值方面的 QoS 约束下最大化用户的保密吞吐量或网络的安全能源效率。在不同的信道知识水平上,我们开发了复杂度低但计算收敛速度快的路径跟踪算法。所提供的模拟不仅显示了所开发算法的效率,还将中断概率与保密程度联系起来。多小区协调波束成形的扩展正在进行中。
有关附录
附录一
提供了有关中断感知用户吞吐量上限和下限的新结果。
OUTAGE PROBABILITY INEQUALITIES
附录二
显示了其他一些结果的保守性,这些结果基于伯恩斯坦型不等式。
BERNSTEIN-TYPE INEQUALITY AND ITS CONSERVATIVENESS
附录 III
中给出了第 III-V 节中使用的一些基本确定性不等式。
BASIC DETERMINISTIC INEQUALITIES


