Car-Following Model
本文介绍的model基于真实的驾驶行为推导而来,比如"与前车保持安全车距","按照期望速度行驶"与"保持舒适的加速"等.此外也考虑了动态的约束,比如刹车距离与车速等.本文主要介绍Gipps和IDM模型,在ACC系统中两种模型使用相同的输入并产生类似的驾驶行为.
模型约束
加速度( a m i c a_{mic} amic,micro微观速度)或速度( v m i c v_{mic} vmic)函数描述驾驶行为,至少可以模型化以下几点:
- 加速度对速度严格递减,且在free场景速度总是加速到理想速度 v 0 v_0 v0:
∂ a m i c ( s , v , v l ) ∂ v < 0 , lim s → ∞ a m i c ( s , v 0 , v l ) = 0 f o r a l l v l \frac{\partial a_{mic}(s, v, v_l)}{\partial v} < 0, \lim_{s \to \infty}a_{mic}(s, v_0, v_l)=0 \ for\ all\ v_l ∂v∂amic(s,v,vl)<0,s→∞limamic(s,v0,vl)=0 for all vl - 加速度是自车到前车距离s的增函数:
∂ a m i c ( s , v , v l ) ∂ s ≥ 0 , lim s → ∞ ∂ a m i c ( s , v , v l ) ∂ s = 0 f o r a l l v l \frac{\partial a_{mic}(s, v, v_l)}{\partial s} \geq 0, \lim_{s \to \infty}\frac{\partial a_{mic}(s, v, v_l)}{\partial s} = 0 \ for\ all \ v_l ∂s∂amic(s,v,vl)≥0,s→∞lim∂s∂amic(s,v,vl)=0 for all vl在他车、障碍物及虚拟障碍物(红绿灯)超出交互距离不会影响到自车行为时等号成立,也即free-flow accelaration:
a f r e e ( v ) = lim s → ∞ a m i c ( s , v , v l ) ≥ a m i c ( s , v , v l ) a_{free}(v) = \lim_{s\to\infty}a_{mic}(s, v, v_l) \geq a_{mic}(s, v, v_l) afree(v)=s→∞limamic(s,v,vl)≥amic(s,v,vl) - 加速度是他车速度的增函数,联合第一条意味着随着接近前车速度加速度会逐渐降低,等号在他车超出了交互距离后成立:
∂ a ~ m i c ( s , v , △ v ) △ v ≤ 0 o r ∂ a ~ m i c ( s , v , v l ) v l ≥ 0 , lim s → ∞ ∂ a ~ m i c ( s , v , v l ) v l = 0 \frac{\partial \tilde{a}_{mic}(s, v, \triangle v)}{\triangle v}\leq0 \ or \ \frac{\partial \tilde{a}_{mic}(s, v, v_l)}{v_l}\geq0, \lim_{s\to\infty}\frac{\partial \tilde{a}_{mic}(s, v, v_l)}{v_l} = 0 △v∂a~mic(s,v,△v)≤0 or vl∂a~mic(s,v,vl)≥0,s→∞limvl∂a~mic(s,v,vl)=0 - 与前车要保持最小距离 s 0 s_0 s0,如果这一距离已经小于 s 0 s_0 s0不能给出负速度:
a m i c ( s , 0 , v l ) = 0 f o r a l l v l ≥ 0 , s ≤ s 0 a_{mic}(s, 0, v_l)=0\ for\ all\ v_l\geq0, s \leq s_0 amic(s,0,vl)=0 for all vl≥0,s≤s0
以上的约束是必要的但并不充分,比如car following场景,与前车需要保持合理的阈值(0.5到3s)。加速度也应该保持在一个舒适的范围( ± 2 m \pm 2m ±2m),至少是一个在车辆机动能力之内的值。尤其在靠近前车时要考虑制动距离与车速的关系。最后model应该能够处理走走停停的非稳态车流,确保不会发生事故,即 s < 0 s<0 s<0.
Gipps 模型
该模型可能是最简单的complete及ancient-freee的模型,使得加速度在一个合理可行的范围内。
safe speed
通过引入safe speed v s a f e ( s , v l ) v_{safe}(s, v_l) vsafe(s,vl)阻止事故的发生,通过前车速度 v l v_l vl及距前车距离s来计算。假定:
- 制动使用常量减速度 b b b,此处不区分舒适减速度与最大减速度;
- 反应时间为常量 △ t \triangle t △t;
- 即使前车突然减速至停止,与前车的距离也不小于最小距离 s 0 s_0 s0;
条件1可得前车的制动距离:
△ x l = v l 2 2 b \triangle x_l = \frac{v_l^2}{2b} △xl=2bvl2
条件2考虑了目标车辆司机的反应时间及制动距离:
△ x = v △ t + v 2 2 b \triangle x = v\triangle t + \frac{v^2}{2b} △x=v△t+2bv2
条件3需满足关系式:
s ≥ s 0 + v △ t + v 2 2 b − v l 2 2 b s\geq s_0 + v\triangle t + \frac{v^2}{2b} -\frac{v_l^2}{2b} s≥s0+v△t+2bv2−2bvl2
通过上式得到safe speed:
v s a f e ( s , v l ) = − b △ t + b 2 △ t 2 + v l 2 + 2 b ( s − s 0 ) v_{safe}(s, v_l) = -b\triangle t + \sqrt{b^2\triangle t^2 + v_l^2 + 2b(s-s_0)} vsafe(s,vl)=−b△t+b2△t2+vl2+2b(s−s0)
model方程
v ( t + △ t ) = m i n [ v + a △ t , v 0 , v s a f e ( s , v l ) ] v(t+\triangle t)=min[v+a\triangle t, v_0, v_{safe}(s, v_l)] v(t+△t)=min[v+a△t,v0,vsafe(s,vl)]
指出几点:
- 仿真更新的时间步长为反应时间 △ t \triangle t △t;
- 目标车辆当前速度超过 v s a f e − a △ t v_{safe}-a\triangle t vsafe−a△t或 v 0 − a △ t v_0 - a\triangle t v0−a△t, 会在下一轮的仿真中降速至 v 0 , v s a f e {v_0, v_{safe}} v0,vsafe中较小的值。
- 否则目标车辆会以减速度a持续减速,直至接近safe speed或者desired speed。
IDM
IDM模型是最简单的完备及free-ancident的模型,基本在所有的单车道交通流场景都能够生成可行的加速度规划及驾驶行为。
模型性质
IDM满足以下条件:
- 首先满足本文开始的5个条件;
- 与前车安全距离要大于 s 0 + v T s_0+vT s0+vT,其中 s 0 s_0 s0是与前车的最小距离,T是与前车的时间差;
- 制动策略,智能控制接近一辆慢车(或者障碍物、红灯等)
- 正常场景,制动尽可能平滑;
- 紧急场景,制度加速度可以超过舒适值直到危险接触,接触危险场景后使用舒适的加速度按照正常场景操作即可;
- 驾驶模式切换要平滑,比如加速模式到跟车模式;等效于加速度函数 a m i c ( s , v , v l ) a_{mic}(s, v, v_l) amic(s,v,vl)对三个自变量是连续可微的;
- 模型要尽可能简洁,每个自变量仅表示驾驶行为的单一维度,以方便模型的调试。
数学表达式
v ˙ = a [ 1 − ( v v 0 ) δ − ( s ∗ ( v , △ v ) s ) 2 ] \dot{v} = a[1-(\frac{v}{v_0})^{\delta} - (\frac{s^{*}(v, \triangle v)}{s})^2] v˙=a[1−(v0v)δ−(ss∗(v,△v))2]
IDM的加速度形式为 a m i c ( s , v , △ v ) a_{mic}(s, v, \triangle v) amic(s,v,△v),包含了两部分;第一部分,当前速度v与期望速度 v 0 v_0 v0比较;第二部分,当前距离s与期望距离 s ∗ s^* s∗的比较。期望距离的计算公式为:
s ∗ ( v , △ ) = s 0 + m a x ( 0 , v T + v △ v 2 a b ) s^*(v, \triangle) = s_0 + max(0, vT+ \frac{v\triangle v}{2\sqrt{ab}}) s∗(v,△)=s0+max(0,vT+2abv△v)
其中, s 0 + v T s_0+vT s0+vT是平衡项, v △ v 2 a b \frac{v\triangle v}{2\sqrt{ab}} 2abv△v是动态项以实现智能制动策略,其中a和b分别表示舒适加速度及减速度;
参数解释
我们通过三个典型场景来说明模型中的参数。
- 由静止在free道路上启动:车辆以最大的加速度a启动,随着速度接近期望速度 v 0 v_0 v0加速度平滑的降为0.加速降低通过参数 δ \delta δ控制,该值越大,速度接近期望速度的过程中加速度越晚减小。
- 跟车模式:最小距离即为安全距离 s 0 + v T s_0+vT s0+vT,包含了最小距离 s 0 s_0 s0及反应时间T
- 接近慢车或静止车时:减速度通常不会超过舒适减速度b

如图,高速与城区驾驶场景的切换仅需修改期望速度即可实现。其他参数可以保持不变用于表示司机的驾驶风格,通常高速驾驶激进的司机在城区也会保持激进风格。相比人类驾驶模式,IDM模型能够更好的表示ACC驾驶模式。不过IDM也很容易就能够适配人类驾驶员的误差估计、反应时间及他车影响评估等方面。
IDM显式的区分了安全时间T、速度调整时间 τ = v 0 / a \tau = v_0/a τ=v0/a及反应时间 T r T_r Tr。
智能制动策略
稳态平衡
通过IDM的加速度函数可得稳态平衡的条件 v ˙ = △ v = 0 \dot{v} = \triangle v = 0 v˙=△v=0:
1 − ( v v 0 ) δ − ( s 0 + v T s ) 2 = 0 1-(\frac{v}{v_0})^{\delta} - (\frac{s_0+vT}{s})^2 = 0 1−(v0v)δ−(ss0+vT)2=0
可得s的解析形式:
s = s e ( v ) = s 0 + v T 1 − ( v v 0 ) δ s=s_e(v)=\frac{s_0+vT}{\sqrt{1-(\frac{v}{v_0})^{\delta} }} s=se(v)=1−(v0v)δs0+vT
改进的加速度函数
IDM模型存在的问题:
- 当前速度超过了目标速度(自车进入限速区),减速度通常会偏大,猛减速;
- 接近目标速度 v 0 v_0 v0时,稳态距离会远超 s 0 + v T s_0+vT s0+vT,从而模型参数T就失去了作用;
- 如果实际车距显著小于目标车距时(cutin场景),制动减速度偏大,猛刹;
当 v > v 0 v>v_0 v>v0时,如果没有紧急情况下要保证减速度的幅值在舒适减速度范围内;最简洁的free acceleration公式为:
a f r e e ( v ) = { a [ 1 − ( v v 0 ) δ ] , i f v ≤ v 0 b [ 1 − ( v v 0 ) a δ b ] , i f v > v 0 a_{free}(v) = \begin{cases} a[1-(\frac{v}{v_0})^{\delta}], \ if\ v\leq v_0\\ b[1-(\frac{v}{v_0})^{\frac{a\delta}{b}}], \ if\ v> v_0 \end{cases} afree(v)={a[1−(v0v)δ], if v≤v0b[1−(v0v)baδ], if v>v0
ACC
为了保留IDM模型的优点,使用CAH加速度来判断IDM模型产生的加速度异常大,再次情况下对ACC系统的加速度函数进行调整。ACC模型做了如下几点假设:
- ACC加速度永远大于IDM模型加速度,因为IDM基于accident-free,给出的加速度总是偏向保守;
- 若CAH与IDM模型产生的加速值一致,则ACC的加速度也为该值;
- 如果IDM生成很大的减速度,而CAH生成的减速度则在舒适值范围内,这种情形并不认为是紧急情形,减速度可以采用CAH的结果
- 如果IDM和CAH生成的加速度都明显超过了舒适值,说明此时是紧急情况,此时ACC加速度则使用二者的最大值。
满足以上条件的ACC模型公式如下:
a A C C = { a I I D M , a I I D M > a C A H ( 1 − c ) a I I D M + c [ a C A H + b t a n h ( a I I D M − a C A H b ) ] , o t h e r w i s e a_{ACC} = \begin{cases} a_{IIDM}, a_{IIDM}>a_{CAH}\\ (1-c)a_{IIDM}+c[a_{CAH}+btanh(\frac{a_{IIDM}-a_{CAH}}{b})],otherwise \end{cases} aACC={aIIDM,aIIDM>aCAH(1−c)aIIDM+c[aCAH+btanh(baIIDM−aCAH)],otherwise
相比IDM/IIDM,ACC模型仅增加了“权重因子”c.ACC模型比较冒进,IIDM模型偏向保守,而权重银子则对二者进行了较好折中。
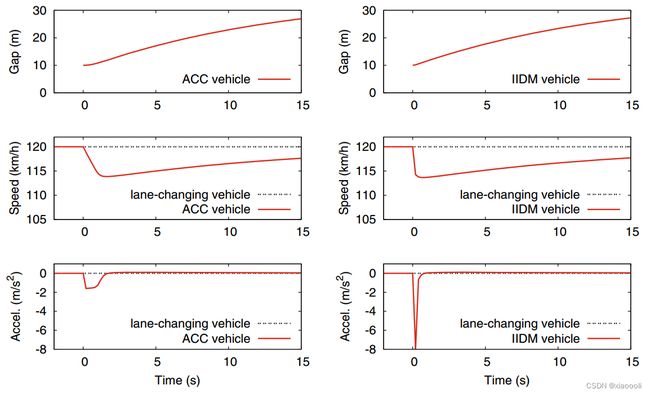
如上图,目标车辆与前车以cutin的方式进入相同车道,但车距为10m,而安全距离应该35m,IIDM模型通常会进行紧急制动,而ACC模型则以舒适的减速度确保安全,反应为平缓。ACC表现出了更加类人的能力。
总而言之,ACC模型是ACC系统的最小完备控制模型。已经运用落地的商用车上,并在测试道路及开放道路上广泛测试。