C++ 数据结构与算法(六)(栈与队列)
栈和队列是STL(C++标准库)里面的两个数据结构。
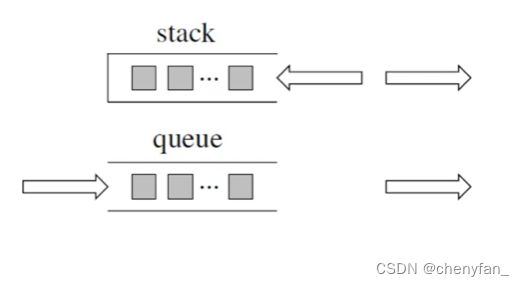
C++标准库是有多个版本的,知道使用的STL是哪个版本,才能知道对应的栈和队列的实现原理。三个最为普遍的STL版本:
- HP STL 其他版本的C++ STL,一般是以HP STL为蓝本实现出来的,HP STL是C++ STL的第一个实现版本,而且开放源代码。
- P.J.Plauger STL 由P.J.Plauger参照HP STL实现出来的,被Visual C++编译器所采用,不是开源的。
- SGI STL 由Silicon Graphics Computer Systems公司参照HP STL实现,被Linux的C++编译器GCC所采用,SGI STL是开源软件,源码可读性甚高。
接下来介绍的栈和队列也是SGI STL里面的数据结构。
栈 stack

栈提供 push,pop,top 等等接口,所有元素必须符合先进后出规则,所以栈不提供走访功能,也不提供迭代器(iterator)。 不像是set 或者map 提供迭代器iterator来遍历所有元素。
栈是以底层容器完成其所有的工作,对外提供统一的接口,底层容器是可插拔的(也就是说我们可以控制使用哪种容器来实现栈的功能)。
所以STL中栈往往不被归类为容器,而被归类为container adapter(容器适配器)。
那么问题来了,STL 中栈是用什么容器实现的?
从下图中可以看出,栈的内部结构,栈的底层实现可以是vector,deque,list 都是可以的, 主要就是数组和链表的底层实现。

我们常用的SGI STL,如果没有指定底层实现的话,默认以deque为缺省情况下栈的底层结构。
deque是一个双向队列,只要封住一段,只开通另一端就可以实现栈的逻辑了。
我们也可以指定vector为栈的底层实现,初始化语句如下:
std::stack<int, std::vector<int> > third; // 使用vector为底层容器的栈
队列 queue
队列中先进先出的数据结构,同样不允许有遍历行为,不提供迭代器, SGI STL中队列一样是以deque为缺省情况下的底部结构。所以STL 队列也不被归类为容器,而被归类为container adapter( 容器适配器)。
也可以指定list 为起底层实现,初始化queue的语句如下:
std::queue<int, std::list<int>> third; // 定义以list为底层容器的队列
232.用栈实现队列 ●
使用栈来模拟队列的行为,需要两个栈,一个输入栈,一个输出栈,这里要注意输入栈和输出栈的关系。在push数据的时候,只要数据放进输入栈就好,但在pop的时候,操作就复杂一些,输出栈如果为空,就把进栈数据全部导入进来(注意是全部导入),再从出栈弹出数据,如果输出栈不为空,则直接从出栈弹出数据就可以了。
class MyQueue {
private:
stack<int> InStack;
stack<int> OutStack;
public:
MyQueue() {
}
void push(int x) {
InStack.push(x);
}
int pop() {
if(OutStack.empty()){
while(!InStack.empty()){
OutStack.push(InStack.top());
InStack.pop();
}
}
int ans = OutStack.top();
OutStack.pop();
return ans;
}
int peek() {
int ans = this->pop(); // peek操作中,实现了pop的代码复用
OutStack.push(ans); // 把pop的元素添加回输出栈
return ans;
}
bool empty() {
return (InStack.empty() && OutStack.empty());
}
};
225. 用队列实现栈 ●
用两个队列来模拟栈,其中一个队列用来备份,用两个队列que1和que2实现队列的功能,把que1最后面的元素以外的元素都备份到que2,然后弹出最后面的元素,此时que1将为下一次操作的备份队列。
class MyStack {
private:
queue<int> Que0;
queue<int> Que1;
int size; // 记录栈的大小
int flag; // 备份标记
int front; // 记录top
public:
MyStack() {
size = 0;
flag = 0;
}
void push(int x) {
if(flag == 1){
Que0.push(x); // Que1 为备份队列
}
else{
Que1.push(x);
}
front = x;
++size;
}
int pop() {
int ans;
if(flag == 1){ // Que1 为备份队列
for(int i = 0; i < size - 1; ++i){
front = Que0.front(); // 弹出前i个元素,并记录top
Que1.push(Que0.front());
Que0.pop();
}
ans = Que0.front();
Que0.pop();
flag = 0;
}
else{
for(int i = 0; i < size - 1; ++i){
front = Que1.front();
Que0.push(Que1.front());
Que1.pop();
}
ans = Que1.front();
Que1.pop();
flag = 1;
}
--size;
return ans;
}
int top() {
return front;
}
bool empty() {
return Que0.empty() && Que1.empty();
}
};
- 优化版(一个队列)
一个队列在模拟栈弹出元素的时候只要将队列头部的元素(除了最后一个元素外) 重新添加到队列尾部,此时在去弹出元素就是栈的顺序了。
class MyStack {
private:
queue<int> Que;
int size; // 记录栈的大小
int front; // 记录top
public:
MyStack() {
size = 0;
}
void push(int x) {
Que.push(x);
front = x;
++size;
}
int pop() {
for(int i = 0; i < size - 1; ++i){
front = Que.front(); // 弹出前i个元素,并记录top
Que.push(Que.front());
Que.pop();
}
int ans = Que.front();
Que.pop();
--size;
return ans;
}
int top() {
return front;
}
bool empty() {
return Que.empty();
}
};
20. 有效的括号 ●
后遇到的左括号要先闭合
-
时间复杂度: O ( n ) O(n) O(n),其中 n 是字符串 s 的长度。
-
空间复杂度: O ( n + ∣ Σ ∣ ) O(n+∣Σ∣) O(n+∣Σ∣),其中 Σ 表示字符集,本题中字符串只包含 6 种括号,∣Σ∣= 6。栈中的字符数量为 O(n),而哈希表使用的空间为 O(∣Σ∣),相加即可得到总空间复杂度。
-
最直接思路: 将左括号压入栈
class Solution {
public:
bool isValid(string s) {
int n = s.size();
if (n % 2 == 1) { // 奇数数组 直接返回false
return false;
}
stack<char> left;
for(char ch : s){
if(ch == '(' || ch == '[' || ch == '{') {
left.push(ch); // 左括号 入栈
}
else if(ch == ')') {
if(!left.empty() && left.top() == '('){ // 右括号 进行匹配判断
left.pop();
}
else{
return false;
}
}
else if(ch == ']') {
if(!left.empty() && left.top() == '['){
left.pop();
}
else{
return false;
}
}
else if(ch == '}') {
if(!left.empty() && left.top() == '{'){
left.pop();
}
else{
return false;
}
}
}
return left.empty();
}
};
- 哈希表存储键值对进行判断优化:
class Solution {
public:
bool isValid(string s) {
int n = s.size();
if (n % 2 == 1) { // 奇数数组 直接返回false
return false;
}
stack<char> left;
unordered_map<char,char> table = {
{')','('}, // 哈希表存储键值对
{']','['},
{'}','{'}
};
for(char ch : s){
if(table.count(ch)){ // 判断是否为右括号
if(left.empty() || left.top() != table[ch]){
return false;
}
left.pop();
}
else{
left.push(ch);
}
}
return left.empty();
}
};
- 将与当前左括号匹配的右括号压入栈
class Solution {
public:
bool isValid(string s) {
stack<char> st;
for(char ch : s){
if(ch == '{'){
st.push('}');
}
else if(ch == '('){
st.push(')');
}
else if(ch == '['){
st.push(']');
}
else{ // 右括号 判断
if(st.empty() || st.top() != ch){
return false;
}
st.pop();
}
}
return st.empty();
}
};
1047. 删除字符串中的所有相邻重复项 ●
输入:“abbaca”
输出:“ca”
直接将string作为栈,利用pop_back和push_back进行栈操作
class Solution {
public:
string removeDuplicates(string s) {
string ans;
for(char ch : s){
if(!ans.empty() && ans.back() == ch){
ans.pop_back();
}
else{
ans.push_back(ch);
}
}
return ans;
}
};
C语言:
char* removeDuplicates(char* s) {
int n = strlen(s);
char* stk = malloc(sizeof(char) * (n + 1));
int retSize = 0;
for (int i = 0; i < n; i++) {
if (retSize > 0 && stk[retSize - 1] == s[i]) {
retSize--;
} else {
stk[retSize++] = s[i];
}
}
stk[retSize] = '\0';
return stk;
}
150. 逆波兰表达式求值 ●●
逆波兰式
class Solution {
public:
int evalRPN(vector<string>& tokens) {
stack<int> st;
int ans = 0;
unordered_set<string> hash {"+","-","*","/"}; // 哈希表,判断是否为符号
for(string str : tokens){
if(hash.count(str)){ // 查找到符号,对栈上前两个数进行处理
int a = st.top();
st.pop();
int b = st.top();
st.pop();
if(str == "+") {st.push(a + b); continue;}
if(str == "*") {st.push(a * b); continue;}
if(str == "/") {st.push(b / a); continue;} // 先出栈作为除数
if(str == "-") {st.push(b - a);} // 先出栈作为减数
}
else{
st.push(stoi(str)); // 字符串转整数 stoi(str),入栈
}
}
return st.top(); // 遍历完成,返回栈顶
}
};
239. 滑动窗口最大值 ●●●
单调双端队列deque
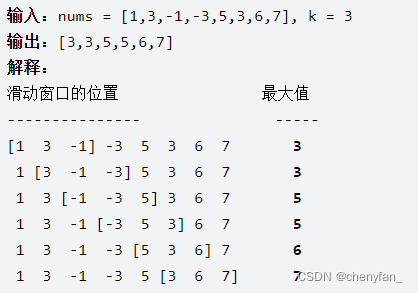
此时我们需要一个队列,放进窗口里的元素,然后随着窗口的移动,队列也一进一出,每次移动之后,队列告诉我们里面的最大值是什么。
队列没有必要维护窗口里的所有元素,只需要维护有可能成为窗口里最大值的元素就可以了,同时保证队里里的元素数值是由大到小的。
那么这个维护元素单调递减的队列就叫做单调队列,即单调递减或单调递增的队列。C++中没有直接支持单调队列,需要我们自己来创建一个单调队列。
pop(value):如果窗口移除的元素value等于单调队列的出口元素,那么队列弹出元素,否则不用任何操作;push(value):如果push的元素value大于入口元素的数值,那么就将队列入口的元素弹出,直到push元素的数值小于等于队列入口元素的数值为止(保持单调特性);- 保持如上规则,每次窗口移动的时候,只要问
que.front()就可以返回当前窗口的最大值。
- 时间复杂度: O ( n ) O(n) O(n),其中 n 是数组 nums 的长度。每一个下标恰好被放入队列一次,并且最多被弹出队列一次,因此时间复杂度为 O(n)。
- 空间复杂度: O ( k ) O(k) O(k)。使用的数据结构是双向的,因此「不断从队首弹出元素」保证了队列中最多不会有超过 k+1 个元素,因此队列使用的空间为 O(k)。
class Solution {
public:
class MyQueue{ // 创建单调双端队列类
public:
deque<int> que;
void pop(int value){ // 当滑动删除的元素等于队列最大值时,将其从队列中删除
if(!que.empty() && value == que.front()){
que.pop_front();
}
}
void push(int value){ // 将元素加入列队,移除更小的元素保持单调特性
while(!que.empty() && value > que.back()){
que.pop_back();
}
que.push_back(value);
}
int front(){ // 返回队列最大值
return que.front();
}
};
vector<int> maxSlidingWindow(vector<int>& nums, int k) {
int n = nums.size();
MyQueue q;
vector<int> ans;
for(int i = 0; i < k; ++i){ // 前k个元素,第一个窗口加入队列
q.push(nums[i]);
}
ans.push_back(q.front()); // 第一个窗口的最大值
for(int j = k; j < n; ++j){ // 移动窗口
q.pop(nums[j-k]); // 处理滑动删除的元素
q.push(nums[j]); // 处理新的元素
ans.push_back(q.front()); // 窗口的最大值
}
return ans;
}
};
347. 前 K 个高频元素 ●●
给你一个整数数组 nums 和一个整数 k ,请你返回其中出现频率前 k 高的元素。你可以按 任意顺序 返回答案。
1. 哈希表+二分(效率低)
class Solution {
public:
vector<int> topKFrequent(vector<int>& nums, int k) {
unordered_map<int, int> hashmap_num; // 哈希表记录元素个数
unordered_map<int, int> hashmap_index; // 哈希表记录元素在ans数组出现的位置
vector<int> ans;
for(int i : nums){
++hashmap_num[i];
if(hashmap_num[i] == 1){
ans.emplace_back(i); // 插入首次出现的元素
hashmap_index[i] = ans.size()-1;
}
else{
int l = 0;
int r = ans.size()-1;
while(l <= r){ // 二分法找到边界位置,注意判断l<=r
int mid = l + (r-l)/2; // 注意下面判断 ans[mid] != i
if(hashmap_num[ans[mid]] > hashmap_num[i]-1 && ans[mid] != i){
l = mid + 1; // l 第一个小于或等于
}else{
r = mid - 1; // r 最后一个大于
}
}
swap(ans[l], ans[hashmap_index[i]]); // 进行位置交换
swap(hashmap_index[ans[hashmap_index[i]]],hashmap_index[i]); // 索引交换
}
}
ans.resize(k);
return ans;
}
};
2. 哈希表
先统计出现最多的次数n,循环减小 n 判断哈希表中 map.second = n 的元素,直到填满 k 个。
class Solution {
public:
vector<int> topKFrequent(vector<int>& nums, int k) {
// first对应元素value second对应元素出现次数
unordered_map<int, int>hashmap;
vector<int> ret;
// 记录元素出现次数
for(int i : nums) hashmap[i]++;
// 找到元素出现的最高频率次数
int maxtimes = 0;
for (auto i : hashmap) {
if (i.second > maxtimes) {
maxtimes = i.second;
}
}
// 从最高往低走 依次输出
while (k > 0){
for (auto i : hashmap){
if (i.second == maxtimes) {
ret.push_back(i.first);
k--;
}
}
maxtimes--;
}
return ret;
}
};
3. 频次 堆排序
建立并维护大小为 k 的小根堆。
总体时间复杂度 O(nlogk):
- 遍历统计元素出现频率 O(n)
- 前k个数构造 规模为 k+1 的最小堆 minheap, O(k), 注意 +1 是因为占位节点。
- 遍历规模 k 之外的数据,大于堆顶则入堆,下沉维护规模为 k 的最小堆 minheap. O(nlogk)
(如需按频率输出,对规模为 k 的堆进行排序)
class Solution {
public:
void sift_up(vector<vector<int>> &heap, int chlid){
vector<int> val = heap[chlid];
while (chlid >> 1 > 0 && val[1] < heap[chlid>>1][1]){
heap[chlid] = heap[chlid>>1];
chlid >>= 1;
heap[chlid] = val;
}
}
void sift_down(vector<vector<int>> &heap, int root, int k){
vector<int> val = heap[root];
while (root << 1 < k){
int chlid = root << 1;
// 注意这里位运算优先级要加括号
if ((chlid|1) < k && heap[chlid|1][1] < heap[chlid][1]) chlid |= 1;
if (heap[chlid][1] < val[1]){
heap[root] = heap[chlid];
root = chlid;
}
else break;
}
heap[root] = val;
}
vector<int> topKFrequent(vector<int>& nums, int k) {
unordered_map<int, int> stat;
for (auto &num : nums) stat[num]++;
vector<vector<int>> vec_stat;
for (auto &item : stat) vec_stat.push_back({item.first, item.second});
vector<vector<int>> heap;
heap.push_back({0, 0});
for (int i = 0; i < k; i++){
heap.push_back(vec_stat[i]);
sift_up(heap, heap.size()-1);
}
for (int i = k; i < vec_stat.size(); i++){
if (vec_stat[i][1] > heap[1][1]){
heap[1] = vec_stat[i];
sift_down(heap, 1, k+1);
}
}
vector<int> result;
for (int i = 1; i < k+1; i++) result.push_back(heap[i][0]);
return result;
}
};
4. 频次 桶排序
统计最大频次,建立大小为 maxCnt 的桶集合。
// 桶排序(根据频率排序)
class Solution {
public:
vector<int> topKFrequent(vector<int>& nums, int k) {
unordered_map<int, int> countMap;
int maxCount = 0;
for (const int& x : nums) {
maxCount = std::max(maxCount, ++countMap[x]); // 利用map统计每个元素的频率,同时得出最大频率
}
vector<vector<int>> buckets(maxCount + 1); // 桶的大小为maxCount+1 (即同一个桶中的元素频率相同)
for (const auto& pair : countMap) {
buckets[pair.second].push_back(pair.first); // 按照map中记录的每个元素频率 将元素放入相应桶中
}
vector<int> result;
for (int i = maxCount; i >= 0 && result.size() < k; --i) { // 从 最后一个桶(频率最高) 往前遍历,从而得出前k个高频元素
for (const auto& x : buckets[i]) {
result.push_back(x);
if (result.size() == k) break;
}
}
return result;
}
};