力扣刷题篇之位运算
系列文章目录
目录
系列文章目录
前言
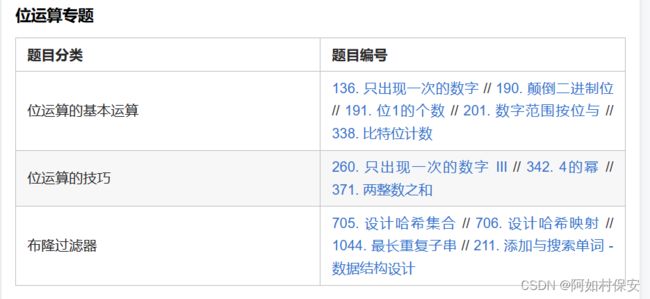
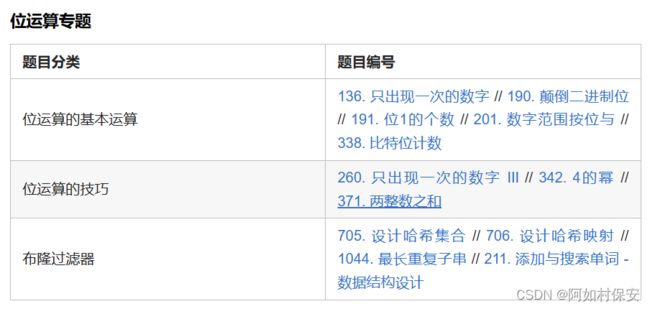
一、位运算的基本运算
二、位运算的技巧
三、布隆过滤器
总结
前言
本系列是个人力扣刷题汇总,本文是数与位。刷题顺序按照[力扣刷题攻略] Re:从零开始的力扣刷题生活 - 力扣(LeetCode)
位运算其实之前的 左程云算法与数据结构代码汇总之排序(Java)-CSDN博客
也有总结到过。 原数异或0等于本身,原数异或本身等于0。异或可以看作无进位相加。
一、位运算的基本运算
136. 只出现一次的数字 - 力扣(LeetCode)
class Solution {
public int singleNumber(int[] nums) {
int result=0;
for(int num:nums){
result=result^num;
}
return result;
}
}
190. 颠倒二进制位 - 力扣(LeetCode)
通过循环,将 result 左移一位,然后将 n 的最低位加到 result 中,最后右移 n,处理下一位。重复这个过程直到处理完 n 的所有位。
public class Solution {
// you need treat n as an unsigned value
public int reverseBits(int n) {
int result = 0;
for (int i = 0; i < 32; i++) {
// 将 result 左移一位,空出最低位
result <<= 1;
// 取 n 的最低位,加到 result 中
result |= (n & 1);
// 右移 n,继续处理下一位
n >>= 1;
}
return result;
}
}
191. 位1的个数 - 力扣(LeetCode)
通过循环,将 n 与 1 进行位与操作,统计最低位是否为 1,然后将 n 右移一位,继续处理下一位,直到 n 的所有位都处理完。
public class Solution {
// you need to treat n as an unsigned value
public int hammingWeight(int n) {
int count = 0;
while (n != 0) {
// 将 n 与 1 进行位与操作,统计最低位是否为 1
count += (n & 1);
// 将 n 右移一位
n >>>= 1;
}
return count;
}
}
201. 数字范围按位与 - 力扣(LeetCode)
通过找到 left 和 right 二进制表示的最长公共前缀来解决。因为对于任何不同的位,按位与的结果一定是 0。
class Solution {
public int rangeBitwiseAnd(int left, int right) {
int shift = 0;
// 找到最长公共前缀
while (left < right) {
left >>= 1;
right >>= 1;
shift++;
}
// 将最长公共前缀左移,右边用零填充
return left << shift;
}
}
338. 比特位计数 - 力扣(LeetCode)
class Solution {
public int[] countBits(int n) {
int[] ans = new int[n+1];
ans[0] = 0;
for(int i = 1; i <= n; i++) {
ans[i] = ans[i >> 1] + i % 2;
}
return ans;
}
}二、位运算的技巧
260. 只出现一次的数字 III - 力扣(LeetCode)
这个之前就总结过了。
先全部异或,再找从右边开始两个数不同的第一位(为1的位);通过&其补码获得,最后分两组进行异或。
class Solution {
public int[] singleNumber(int[] nums) {
int xorAll = 0;
for(int x:nums){
xorAll ^= x;
}
int lowBit = xorAll & -xorAll;
int[] ans = new int[2];
int a1 = 0, a2 = 0;
for(int x:nums){
if((x & lowBit) != 0){
a1 ^= x;
}else{
a2 ^= x;
}
}
return new int[]{a1,a2};
}
}342. 4的幂 - 力扣(LeetCode)
class Solution {
public boolean isPowerOfFour(int n) {
long i = 1;
while(i < n){
i*=4;
}
return i == n;
}
}
371. 两整数之和 - 力扣(LeetCode)
利用了异或运算和与运算的性质,避免使用传统的加法运算符。
class Solution {
public int getSum(int a, int b) {
//当进位数没有了,证明计算完成
while (b != 0) {
//计算不进位的数
int tempA = a ^ b;
//计算进位的数
int tempB = (a & b) << 1;
a = tempA;
b = tempB;
}
return a;
}
}三、布隆过滤器
705. 设计哈希集合 - 力扣(LeetCode)
这种之前哈希表已经总结过了
class MyHashSet {
/** Initialize your data structure here. */
boolean[] map = new boolean[1000005];
public MyHashSet() {
}
public void add(int key) {
map[key] = true;
}
public void remove(int key) {
map[key] = false;
}
/** Returns true if this set contains the specified element */
public boolean contains(int key) {
return map[key] == true;
}
}
/**
* Your MyHashSet object will be instantiated and called as such:
* MyHashSet obj = new MyHashSet();
* obj.add(key);
* obj.remove(key);
* boolean param_3 = obj.contains(key);
*/// class MyHashSet {
// /** Initialize your data structure here. */
// boolean[] map = new boolean[1000005];
// public MyHashSet() {
// }
// public void add(int key) {
// map[key] = true;
// }
// public void remove(int key) {
// map[key] = false;
// }
// /** Returns true if this set contains the specified element */
// public boolean contains(int key) {
// return map[key] == true;
// }
// }
// /**
// * Your MyHashSet object will be instantiated and called as such:
// * MyHashSet obj = new MyHashSet();
// * obj.add(key);
// * obj.remove(key);
// * boolean param_3 = obj.contains(key);
// */
class MyHashSet {
private static final int BASE = 769;
private LinkedList[] data;
/** Initialize your data structure here. */
public MyHashSet() {
data = new LinkedList[BASE];
for (int i = 0; i < BASE; ++i) {
data[i] = new LinkedList();
}
}
public void add(int key) {
int h = hash(key);
Iterator iterator = data[h].iterator();
while (iterator.hasNext()) {
Integer element = iterator.next();
if (element == key) {
return;
}
}
data[h].offerLast(key);
}
public void remove(int key) {
int h = hash(key);
Iterator iterator = data[h].iterator();
while (iterator.hasNext()) {
Integer element = iterator.next();
if (element == key) {
data[h].remove(element);
return;
}
}
}
/** Returns true if this set contains the specified element */
public boolean contains(int key) {
int h = hash(key);
Iterator iterator = data[h].iterator();
while (iterator.hasNext()) {
Integer element = iterator.next();
if (element == key) {
return true;
}
}
return false;
}
private static int hash(int key) {
return key % BASE;
}
}
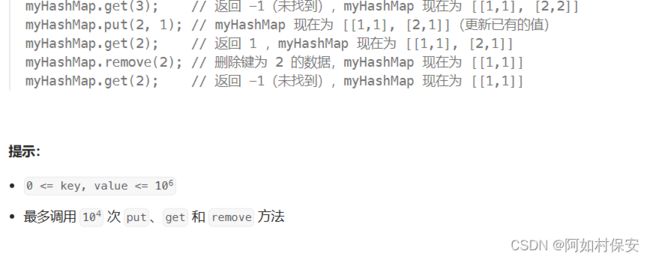
706. 设计哈希映射 - 力扣(LeetCode)
class MyHashMap {
static int n=6774;
int[] s;
int[] v;
public MyHashMap() {
s=new int[n];
v=new int[n];
Arrays.fill(s,n);
}
public void put(int key, int value) {
int k=f(key);
s[k]=key;
v[k]=value;
}
public int get(int key) {
int k=f(key);
if(s[k]==n) return -1;
return v[k];
}
public void remove(int key) {
v[f(key)]=-1;
}
public int f(int x){
int k=x%n;
while(s[k]!=x&&s[k]!=n){
k++;
if(k==n) k=0;
}
return k;
}
}
/**
* Your MyHashMap object will be instantiated and called as such:
* MyHashMap obj = new MyHashMap();
* obj.put(key,value);
* int param_2 = obj.get(key);
* obj.remove(key);
*/
1044. 最长重复子串 - 力扣(LeetCode)
基于DC3算法的后缀数组构建,并使用后缀数组求解最长重复子串问题
DC3算法,该算法用于构建后缀数组。后缀数组构建完成后,根据height数组找到最长的重复子串。这个还要仔细研究
class Solution {
public static String longestDupSubstring(String s) {
int length = s.length();
int[] arr = new int[length];
for (int i = 0; i < length; i++) {
arr[i] = s.charAt(i);
}
DC3 dc3 = new DC3(arr);
int[] height = dc3.getHeight();
int[] suffix = dc3.getSuffix();
int max = height[0];// height中的最大值
int maxIndex = -1;// height中的最大值的下标
for (int i = 1; i < length; i++) {
if (height[i] > max) {
maxIndex = i;
max = height[i];
}
}
return maxIndex == -1 ? "" : s.substring(suffix[maxIndex]).substring(0, max);
}
private static class DC3{
private final int[] suffix;// 后缀数组,里面的元素按照字典序从小到大排.suffix[a]=b表示b对应的后缀排第a名
private final int[] rank;// suffix的伴生数组,含义和suffix相反.rank[a]=b表示a对应的后缀排第b名
private final int[] height;// height[i]表示第i名后缀和第i-1名后缀的最长公共前缀的长度,i从0开始,i表示名次
public int[] getSuffix() {
return suffix;
}
public int[] getRank() {
return rank;
}
public int[] getHeight() {
return height;
}
public DC3(int[] arr) {
suffix = suffix(arr);// 求arr的后缀数组
rank = rank(suffix);
height = height(arr);
}
private int[] height(int[] arr) {
int length = arr.length;
int[] result = new int[length];
for (int i = 0, value = 0; i < length; i++) {
if (rank[i] != 0) {
if (value > 0) {
value--;
}
int pre = suffix[rank[i] - 1];
while (i + value < length && pre + value < length && arr[i + value] == arr[pre + value]) {
value++;
}
result[rank[i]] = value;
}
}
return result;
}
private int[] rank(int[] suffix) {
int length = suffix.length;
int[] result = new int[length];
// 将suffix数组的下标和元素值互换即可
for (int i = 0; i < length; i++) {
result[suffix[i]] = i;
}
return result;
}
private int[] suffix(int[] arr) {
int max = getMax(arr);
int length = arr.length;
int[] newArr = new int[length + 3];
System.arraycopy(arr, 0, newArr, 0, length);
return skew(newArr, length, max + 1);
}
private int[] skew(int[] arr, int length, int num) {
// eg:下标为0,3,6,9,12...属于s0类;下标为1,4,7,10,13...属于s1类;下标为2,5,8,11,14...属于s2类;
int n0 = (length + 2) / 3;// s0类个数
int n1 = (length + 1) / 3;// s1类个数
int n2 = length / 3;// s2类个数
int n02 = n0 + n2;// s02类的个数
// 按照定义,n0个数要么比n1和n2多1个,要么相等.因此s12的大小用n02而不是n12是为了处理边界条件,防止数组越界判断
int[] s12 = new int[n02 + 3];
int[] sf12 = new int[n02 + 3];// 记录s12类的排名
// 统计s12类下标都有哪些,放到s12中
for (int i = 0, j = 0; i < length + (n0 - n1); i++) {
if (i % 3 != 0) {
s12[j++] = i;
}
}
// 将s12类排序,排序结果最终会放到sf12中
radixPass(arr, s12, sf12, 2, n02, num);// 按照"个位数"排序,结果放到sf12中
radixPass(arr, sf12, s12, 1, n02, num);// 按照"十位数"排序,结果放到s12中
radixPass(arr, s12, sf12, 0, n02, num);// 按照"百位数"排序,结果放到sf12中
int rank = 0; // 记录了排名
int ascii1 = -1, ascii2 = -1, ascii3 = -1;// 记录了3个字符的ascii码
for (int i = 0; i < n02; i++) {
if (ascii1 != arr[sf12[i]] || ascii2 != arr[sf12[i] + 1] || ascii3 != arr[sf12[i] + 2]) {
rank++;
ascii1 = arr[sf12[i]];
ascii2 = arr[sf12[i] + 1];
ascii3 = arr[sf12[i] + 2];
}
if (sf12[i] % 3 == 1) {
s12[sf12[i] / 3] = rank;// 计算s1类的排名
} else {// sf12[i]的值只有s1或s2类的,因此走到这里必定是s2类的
s12[sf12[i] / 3 + n0] = rank;// 计算s2类的排名
}
}
if (rank < n02) {
sf12 = skew(s12, n02, rank + 1);// 递归调用直到有序,有序的排名结果放到sf12中
for (int i = 0; i < n02; i++) {
s12[sf12[i]] = i + 1;
}
} else {// 若s12已经有序了,则根据s12直接得到sf12即可
for (int i = 0; i < n02; i++) {
sf12[s12[i] - 1] = i;
}
}
// 对s0类进行排序,排序结果放到sf0中
int[] s0 = new int[n0];
int[] sf0 = new int[n0];
for (int i = 0, j = 0; i < n02; i++) {
if (sf12[i] < n0) {
s0[j++] = 3 * sf12[i];
}
}
radixPass(arr, s0, sf0, 0, n0, num);
int[] suffix = new int[length];// 记录最终排序
for (int p = 0, t = n0 - n1, k = 0; k < length; k++) {
int i = sf12[t] < n0 ? sf12[t] * 3 + 1 : (sf12[t] - n0) * 3 + 2;
int j = sf0[p];
if (sf12[t] < n0 ? abOrder(arr[i], s12[sf12[t] + n0], arr[j], s12[j / 3])
: abOrder(arr[i], arr[i + 1], s12[sf12[t] - n0 + 1], arr[j], arr[j + 1], s12[j / 3 + n0])) {
suffix[k] = i;
t++;
if (t == n02) {
for (k++; p < n0; p++, k++) {
suffix[k] = sf0[p];
}
}
} else {
suffix[k] = j;
p++;
if (p == n0) {
for (k++; t < n02; t++, k++) {
suffix[k] = sf12[t] < n0 ? sf12[t] * 3 + 1 : (sf12[t] - n0) * 3 + 2;
}
}
}
}
return suffix;
}
private void radixPass(int[] arr, int[] input, int[] output, int offset, int limit, int num) {
int[] barrel = new int[num];// 桶
// 统计各个桶中元素的数量
for (int i = 0; i < limit; i++) {
barrel[arr[input[i] + offset]]++;
}
for (int i = 0, sum = 0; i < num; i++) {
int temp = barrel[i];
barrel[i] = sum;
sum += temp;
}
// 将本趟基排结果放到output中
for (int i = 0; i < limit; i++) {
output[barrel[arr[input[i] + offset]]++] = input[i];
}
}
// 比较(x1,y1)和(x2,y2)的字典序,前者<=后者返回true
private boolean abOrder(int x1, int y1, int x2, int y2) {
return (x1 < x2) || (x1 == x2 && y1 <= y2);
}
// 比较(x1,y1,z1)和(x2,y2,z2)的字典序,前者<=后者返回true
private boolean abOrder(int x1, int y1, int z1, int x2, int y2, int z2) {
return (x1 < x2) || (x1 == x2 && abOrder(y1, z1, y2, z2));
}
// 获取数组的最大值
private int getMax(int[] arr) {
int max = Integer.MIN_VALUE;
for (int i : arr) {
max = Math.max(max, i);
}
return max;
}
}
}
211. 添加与搜索单词 - 数据结构设计 - 力扣(LeetCode)
class WordDictionary {
private WordDictionary[] items; // 数组用于存储子节点
boolean isEnd; // 表示当前节点是否是一个单词的结束节点
public WordDictionary() {
items = new WordDictionary[26]; // 初始化子节点数组
}
// 向 WordDictionary 中添加单词
public void addWord(String word) {
WordDictionary curr = this;
int n = word.length();
// 逐个字母遍历单词
for (int i = 0; i < n; i++) {
int index = word.charAt(i) - 'a';
// 如果当前节点的子节点数组中没有对应字母的节点,则创建一个新的节点
if (curr.items[index] == null) {
curr.items[index] = new WordDictionary();
}
curr = curr.items[index]; // 继续向下遍历
}
curr.isEnd = true; // 将单词的最后一个字母节点的 isEnd 设置为 true,表示这是一个单词的结束
}
// 搜索给定的单词
public boolean search(String word) {
return search(this, word, 0);
}
// 递归搜索单词
private boolean search(WordDictionary curr, String word, int start) {
int n = word.length();
// 如果已经遍历完单词,判断当前节点是否是一个单词的结束节点
if (start == n) {
return curr.isEnd;
}
char c = word.charAt(start);
// 如果当前字母不是通配符 '.',直接查找对应的子节点
if (c != '.') {
WordDictionary item = curr.items[c - 'a'];
return item != null && search(item, word, start + 1);
}
// 如果字母是通配符 '.',遍历当前节点的所有子节点,递归调用 search 方法
for (int j = 0; j < 26; j++) {
if (curr.items[j] != null && search(curr.items[j], word, start + 1)) {
return true;
}
}
return false;
}
}
总结
布隆过滤器这里难一点,其他都很简单,开心!
DC3算法还要去搞清楚一下。