互信息法确定时间序列最佳时延

1 代码实现

最近需要实现对时间序列的相空间重构，参考ChatGPT与相关论文，实现了基于互信息法确定时间序列最佳时延的程序，代码如下：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

N_ft = 1000

def delay_time(data, max_delay=10):
    # 1. 计算自信息和联合信息
    ts = pd.Series(data)
    delays = range(1, max_delay+1)
    # ics = [ts.autocorr(d) for d in delays]   # 自信息

    ics = [ts.shift(d).autocorr() for d in delays]
    jcs = []
    for d in delays:
        jcs.append(ts.corr(ts.shift(d)))     # 联合信息

    # 2. 计算互信息
    print(ics)
    print(jcs)
    mis = []
    for jc, ic in zip(jcs, ics):
        print(jc, ic)
        mi = -0.5*np.log(1-jc**2)+0.5*np.log(1-ic**2) # 互信息
        print(mi)
        mis.append(mi)

    # 3. 找到第一个局部极小值并返回其对应的时延
    diffs = np.diff(mis)
    print(diffs)
    i = np.where(diffs > 0)[0][0]
    delay = delays[i]

    # 可视化互信息函数
    plt.plot(delays[0:], mis, 'bo-')
    plt.xlabel('Delay(τ)')
    plt.ylabel('Mutual Information(I(τ))')
    plt.grid(axis='x')
    plt.grid(axis='y')
    plt.axvline(x=delay, color='r', linestyle='--')
    plt.show()

    return delay

t = []
f1 = 25
f2 = 30
for i in range(N_ft):
    t.append(i * 0.001)
t = np.array(t)
# yu = np.ones(M * N)
AEall = np.sin(t * 2 * np.pi * f1) + np.sin(t * 2 * np.pi * f2)  #在这里直接改信号

delay = delay_time(AEall, max_delay=30)
print('Delay time:', delay)

运行结果如图所示：
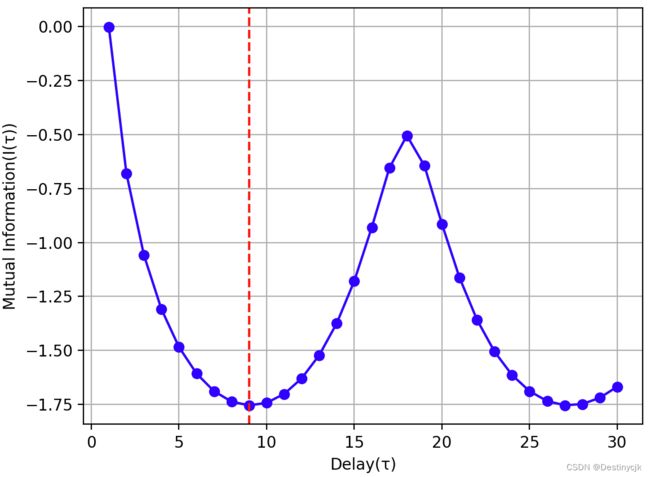根据论文《混沌时间序列预测研究及应用》，寻找第一个局部极小值点确定为最佳时延，即该序列最佳时延为9.

2 相关说明

程序中相关公式为chatGPT提供，其正确性可能有待进一步确定。使用过程中若有问题，欢迎大家一起讨论！另外，在完成最佳时延的确定后，需要完成最佳嵌入维数的确定，可参考博客，这里，对其中GP算法的实现作出略微修改，代码如下：

import numpy as np
from scipy.fftpack import fft
from scipy import fftpack
import matplotlib.pyplot as plt
import pandas as pd

N_ft = 1000

# GP算法求关联维数(时频域特征)
def GP(imf, tau):
    if (len(imf) != N_ft):
        print('请输入指定的数据长度！')  # 需要更改，比如弹出对话框
        return
    elif (isinstance(imf, np.ndarray) != True):
        print('数据格式错误！')
        return
    else:
        m_max = 10  # 最大嵌入维数
        ss = 50  # r的步长
        fig = plt.figure(1)
        for m in range(1, m_max + 1):
            i_num = N_ft - (m - 1) * tau
            kj_m = np.zeros((i_num, m))  # m维重构相空间
            for i in range(i_num):
                for j in range(m):
                    kj_m[i][j] = imf[i + j * tau]
            dist_min, dist_max = np.linalg.norm(kj_m[0] - kj_m[1]), np.linalg.norm(kj_m[0] - kj_m[1])
            Dist_m = np.zeros((i_num, i_num))  # 两向量之间的距离
            for i in range(i_num):
                for k in range(i_num):
                    D = np.linalg.norm(kj_m[i] - kj_m[k])
                    if (D > dist_max):
                        dist_max = D
                    elif (D > 0 and D < dist_min):
                        dist_min = D
                    Dist_m[i][k] = D
            dr = (dist_max - dist_min) / (ss - 1)  # r的间距
            r_m = []
            Cr_m = []
            for r_index in range(ss):
                r = dist_min + r_index * dr
                r_m.append(r)
                Temp = np.heaviside(r - Dist_m, 1)
                for i in range(i_num):
                    Temp[i][i] = 0
                Cr_m.append(np.sum(Temp))
            r_m = np.log(np.array((r_m)))
            print(r_m)
            Cr_m = np.log(np.array((Cr_m)) / (i_num * (i_num - 1)))
            print(Cr_m)
            plt.plot(r_m, Cr_m, label = str(m))
        plt.xlabel('ln(r)', fontsize=18)
        plt.ylabel('ln(C)', fontsize=18)
        plt.xticks(fontsize=16)
        plt.yticks(fontsize=16)
        plt.legend(fontsize=15)
        plt.show()

if __name__=='__main__':
    # 检验关联维数程序
    t = []
    f1 = 25
    f2 = 30
    for i in range(N_ft):
        t.append(i * 0.001)
    t = np.array(t)

    # yu = np.ones(M * N)
    AEall = np.sin(t * 2 * np.pi * f1) + np.sin(t * 2 * np.pi * f2)  #在这里直接改信号
    GP(AEall, 1)

代码运行结果如下：
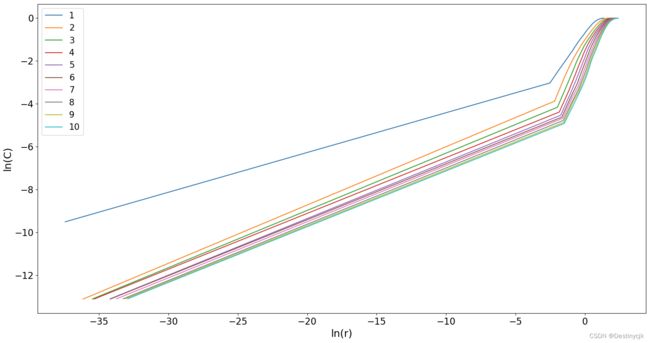同样，结合论文中对GP算法确定最佳嵌入维数的介绍，曲线中线性部分的斜率一般会随着m的增大而增大，当斜率不再增大而趋于稳定时，即为饱和关联维，此时对应的m即为最佳嵌入维。至此，完成对最佳时延与嵌入维数的确定，基于这两个参数完成对时序的相空间重构。

3 参考资料

[1] 高俊杰. 混沌时间序列预测研究及应用[D].上海交通大学,2013.
[2] Python实现相空间重构求关联维数：https://blog.csdn.net/Lwwwwwwwl/article/details/111410179.