算法 时间、空间复杂度的计算（C语言/小白/零基础/新手 + 例题）

目录

1. 时间复杂度

计算时间复杂度（ O(N）)的方法：

  例1：嵌套循环时间复杂度的计算   

  例2：双重循环时间复杂度的计算

  例3：常熟循环的时间复杂度

  例6：冒泡排序的时间复杂度

  例7： 二分查找的时间复杂度

  例8：斐波那契的时间复杂度

        常见的时间复杂度：

2. 空间复杂度

  例1：创建变量

例2：长度N的数组

例3：斐波那契的空间复杂度

3. OJ：消失的数字

---

1. 时间复杂度

        算法在编写成可执行程序后，运行时所需要消耗时间资源和空间( 内存 )资源。因此衡量一个算法的好坏，一般是从时间和空间两个维度进行衡量，即时间复杂度 和 空间复杂度。、

        时间复杂度主要衡量一个算法的快慢。

        大O的渐进表示法：大O符号，是用于描述函数渐进行为的数学符号。

计算时间复杂度（ O(N）)的方法：

        1. 用常熟1代替所有运行时间中的加法常数；

        2. 在修改后的运行时间中，只保留最高项；

        3. 如果最高项存在且不是1，则去除最高项的系数。

        有个重要的点是，大家算时间复杂度的时候，不要去关注代码，要去思考算法的思路！！！，其次我们这次所说的时间复杂度都是指最坏时间复杂度。

  例1：嵌套循环时间复杂度的计算   

int Test(int N)
{
	int count = 0;
	for (int i = 0;i < N;i++)
	{
		for (int j = 0;j < N;j++)
		{
			count++;
		}
	}
	int num 10;
	while (num--)
	{
		count++;
	}
	return count;
}

         O(N)  = N * N  + 10 ，只看最高次项，即为N^2

        时间复杂度: T(N) = O(N^2)。

  例2：双重循环时间复杂度的计算

int Test(int N,int M)
{
	int count = 0;
	for (int i = 0;i < N;i++)
	{
		count++;
	}
	for (int j = 0;j < m;j++)
	{
		count++;
	}
	return count;
}

          时间复杂度: T(N) = O(N + M)。

        这里没有说明M 和 N 的大小关系，如果M > N，则时间复杂度为 O(M)，反之，则相反。

  例3：常熟循环的时间复杂度

int Test(int N,int M)
{
	int count = 0;
	for (int i = 0;i < 100 ; i++)
	{
		count++;
	}
	return count;
}

            时间复杂度: T(N) = O(1)。

        这里的1不是指数字1，只执行1次，而是指常数次。即所有常数项均用1代替。

  例6：冒泡排序的时间复杂度

int Test(int* nums,int N)
{
	int count = 0;
	for (int i = 0;i < N;i++)
	{
		for (int j = 0;j < i;j++)
		{
			if (nums[j] > nums[j + 1])
			{
				int t = nums[j];
				nums[j] = nums[j+1];
				nums[j + 1] = t;
			}
		}
	}
	return count;
}

         时间复杂度: T(N) = O(N^2)。

         冒泡排序的时间复杂度计算是等差数列相加，首相是n-1 ，尾项是 1，项数为n-1，所以运行时间公式为 N*(N-1) / 2，只保留最高次项N^2/2，且最高次项的系数为1。

        这里就很能体现我们不只能看代码的循环次数。

  例7： 二分查找的时间复杂度

int Binary_search(SqList L,ElemType key)
{
	int low = 0;int mid = 0;int high = L.length-1;
	while(low<=high)
	{
		mid = (low+high)/2;
 		if(key==L.data[mid])
		{
			return mid;
		}
		else if(key>L.data[mid])
		{
			low = mid+1;
		}
		else
		{
			high = mid-1;
		}
	}
	return -1;
}

           时间复杂度: T(N) = O(log N)。

            这里log是省略2的。执行次数X，数组长度N，每次查找长度/2,，得出2^X = N,所以执行次数X = logN。

  例8：斐波那契的时间复杂度

        时间复杂度，是累加的，毕竟时间一去不复返。

int Fib(int N)
{
    if(N < 3)
     {
        return 1;
     }
    return Fac(N-1) + Fib(N-2);
}

         时间复杂度: T(N) = O(2 ^ N)。

       

        可以看出，斐波那契数列的时间复杂度就是等比数列求和，代入公式，利用大O渐进表示法规则，我们可以得出时间复杂度为 2^n。

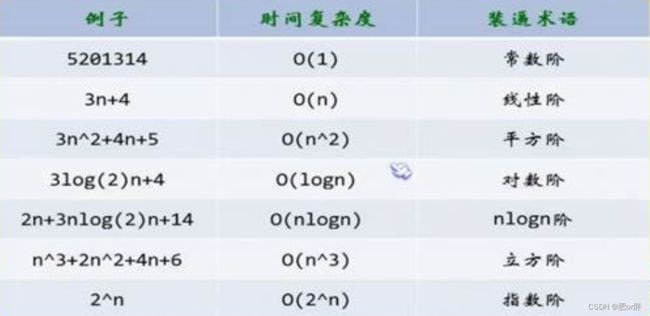
        常见的时间复杂度：

        

        O(1) < O(logN) < O(n) < O(NlogN) < O(N^2) < O(N^3) < O(2^N) < O(N !) < O(N^N)

2. 空间复杂度

        空间复杂，是对一个算法在运行过程中临时额外开辟占用的存储空间大小维度。

        空间复杂度不是程序占了多少字节，而是算的变量的数量。与时间复杂度一样，同样都采用大O渐进法表示。

        注意：函数运行时所需要的栈空间（形参，寄存器信息等）在编译期间已经确定好了，因此，空间复杂度主要通过函数在运行时申请的额外空间来确定。

        目前，随着硬件设备的提升，我们对空间复杂度不是那么关注，所以我们对代码的衡量主要关注时间复杂度。这就意味着，我们可以用空间换时间的思路，大家做题的时候，可以尝试使用一下这个思路。

  例1：创建变量

void Test(int N)
{
	int a =0;
    int b =0;
    for(int i=0;i<10;i++)
    {
        a++;
        b++;
    }
}

         空间复杂度：S(N) = O(1)

        这里1，指的是常数个变量。而不是数字1，仅有1个变量的意思。

例2：长度N的数组

void Test(int N)
{
	int* nums = (int*)malloc(sizeof(int) * N);
    for(int i=0;i

              空间复杂度：S(N) = O(N)、

                有N个变量，所以空间复杂度为N

例3：斐波那契的空间复杂度

int Fib(int N)
{
    if(N < 3)
     {
        return 1;
     }
    return Fac(N-1) + Fib(N-2);
}

            空间复杂度：S(N) = O( N)、            

           这里涉及函数栈帧的创建和销毁，大家简单的理解为，每个函数创建使用的时候都要在内存中开辟栈帧空间，函数结束时也会销毁栈帧空间。这就意味着，空间我们可以重复利用。

           当我们使用Fib(1)函数时，开辟空间，结束时，释放销毁空间，Fib(2)函数使用时可以使用Fib(1)函数销毁的函数。

3. OJ：消失的数字

面试题 17.04. 消失的数字 - 力扣（LeetCode）

数组nums包含从0到n的所有整数，但其中缺了一个。请编写代码找出那个缺失的整数。你有办法在O(n)时间内完成吗？

注意：本题相对书上原题稍作改动

示例 1：

输入：[3,0,1]
输出：2

示例 2：

输入：[9,6,4,2,3,5,7,0,1]
输出：8

//1
int missingNumber(int* nums, int numsSize){
    int ret = 0;
    for(int i=0;i<=numsSize;i++)
    {
        ret+=i;
    }
    for(int i=0;i