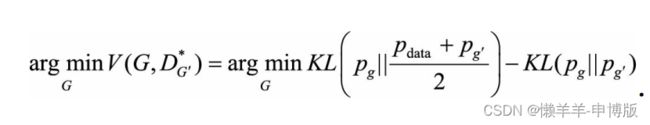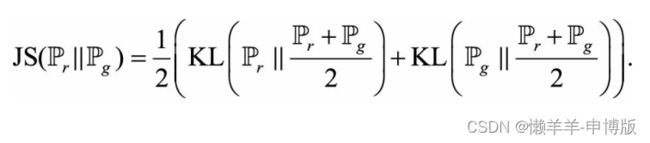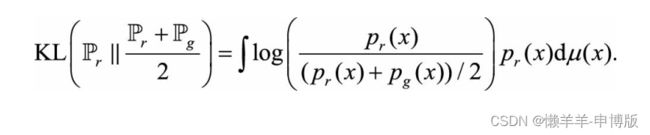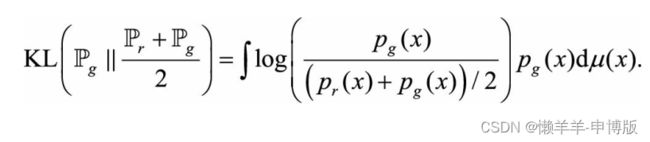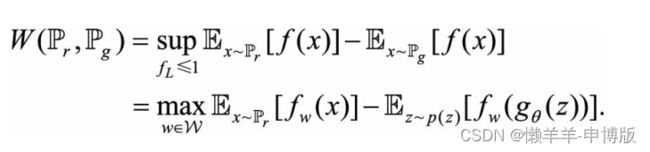【机器学习13】生成对抗网络
1 GANs的基本思想和训练过程
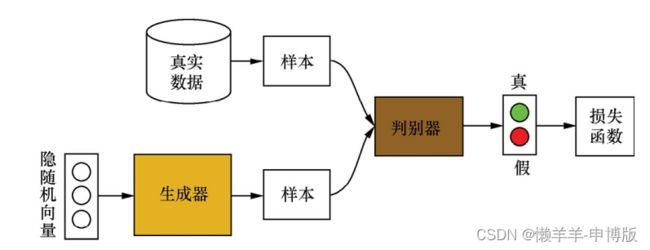
生成器用于合成“假”样本, 判别器用于判断输入的样本是真实的还是合成的。 生成器从先验分布中采得随机信号,经过神经网络的变换, 得到模拟样本; 判别器既接收来自生成器的模拟样本, 也接收来自实际数据集的真实样本。
GANs采用对抗策略进行模型训练, 一方面, 生成器通过调节自身参数, 使得其生成的样本尽量难以被判别器识别出是真实样本还是模拟样本; 另一方面, 判别器通过调节自身参数, 使得其能尽可能准确地判别出输入样本的来源。
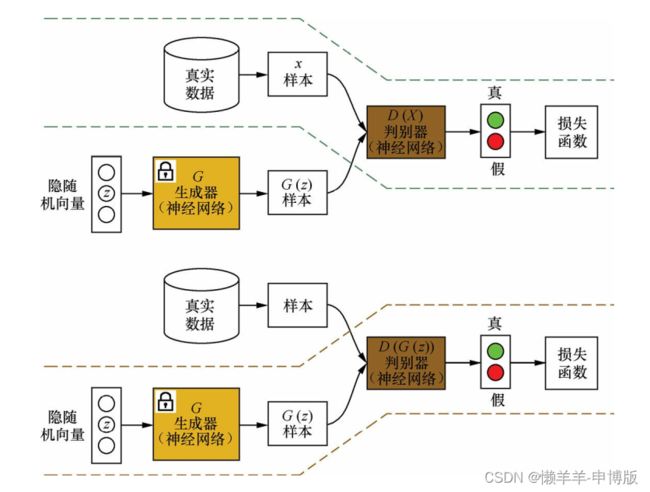
(1) 在训练判别器时, 先固定生成器G(·); 然后利用生成器随机模拟产生样本G(z)作为负样本(z是一个随机向量) , 并从真实数据集中采样获得正样本X; 将这些正负样本输入到判别器D(·)中, 根据判别器的输出(即D(X)或D(G(z))) 和样本标签来计算误差; 最后利用误差反向传播算法来更新判别器D(·)的参数
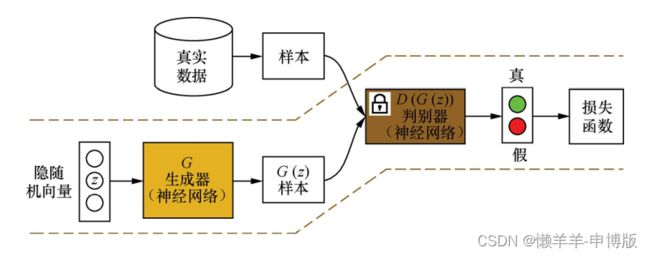
(2) 在训练生成器时, 先固定判别器D(·); 然后利用当前生成器G(·)随机模拟产生样本G(z), 并输入到判别器D(·)中; 根据判别器的输出D(G(z))和样本标签来计算误差, 最后利用误差反向传播算法来更新生成器G(·)的参数
2 GANs的值函数
2.1 均衡点时的解(G*,D*)和值函数
因为判别器D试图识别实际数据为真实样本, 识别生成器生成的数据为模拟样本, 所以这是一个二分类问题, 损失函数写成:
其中D(x)表示判别器预测x为真实样本的概率, p(data|x)和p(g|x)表示x分属真实数据集和生成器这两类的概率。 样本x的来源一半是实际数据集, 一半是生成器。
2.2 在未达到均衡点时, 将生成器G固定, 寻找当下最优的判别器DG*, 请给出DG*和此时的值函数
要了解 Jensen-Shannon 散度(JSD)的定义。给定两个概率分布 P 和 Q,JSD 定义如下:
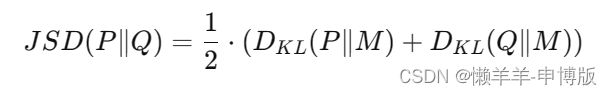
此时,
由此看出, 优化生成器G实际是在最小化生成样本分布与真实样本分布的JS距离。
2.3 固定D而将G优化到底, 解GD*和此时的值函数
3 WGAN
3.1 原GANS存在的问题
坍缩模式:拿图片举例, 反复生成一些相近或相同的图片,多样性太差。 生成器似乎将图片记下, 没有泛化, 更没有造新图的能力。
考虑生成器分布与真实数据分布的JS距离, 即两个KL距离的平均:
第一个KL距离:
高维空间绝大部分地方见不到真实数据, pr(x)处处为零, 对KL距离的贡献为零;即使在真实数据蜷缩的低维空间, 高维空间会忽略低维空间的体积, 概率上讲测度为零。 KL距离就成了:
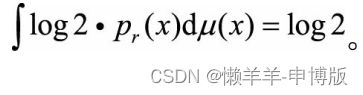
再看第二个KL距离:
同理也是log2。
因此无论生成器怎么训练,JS距离都是一个常数,对生成器的梯度为0.
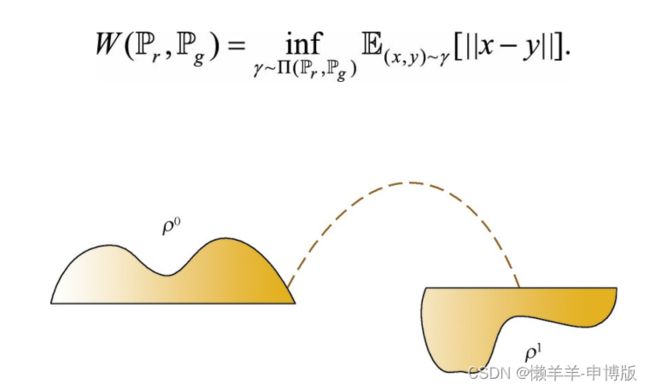
3.2 Wasserstein距离(推土机距离)
不管真实分布藏在哪个低维子空间里, 生成器都能感知它在哪, 因为生成器只要将自身分布稍做变化, 就会改变它到真实分布的推土机距离; 而JS距离是不敏感的, 无论生成器怎么变化, JS距离都是一个常数。 因此, 使用推土机距离, 能有效锁定低维子空间中的真实数据分布。
3.3 WGAN
这里的f与D不同, 前者要满足|| f ||L≤1, 即1-Lipschitz函数,后者是一个Sigmoid函数作输出层的神经网络。 Sigmoid函数的值有天然的界, 而1-Lipschitz不是限制函数值的界, 而是限制函数导数的界, 使得函数在每点上的变化率不能无限大。 神经网络里如何体现1-Lipschitz或K-Lipschitz呢? WGAN的思路很巧妙, 在一个前向神经网络里, 输入经过多次线性变换和非线性激活函数得到输出, 输出对输入的梯度, 绝大部分都是由线性操作所乘的权重矩阵贡献的, 因此约束每个权重矩阵的大小, 可以约束网络输出对输入的梯度大小。
判别器在这里换了一个名字, 叫评分器(Critic) , 目标函数由“区分样本来源”变成“为样本打分”: 越像真实样本分数越高, 否则越低。
4 DCGAN
4.1 在生成器和判别器中应该怎样设计深层卷积结构?
4.1.1 生成器
生成器生成图片, 可以看成图片分类的一个逆过程。 图片分类器的输入是一张图片, 输出是一个类别; 图片生成器的输出是一张图片,输入通常有一个随机向量。
用随机向量的每维刻画不同的细节, 然后生成一张图片。 随机向量不含像素级别的位置信息, 但是对于图片, 每个像素都有它的位置, 点构成了线, 线组成了面, 进而描绘出物体的形状。 如果这些位置信息不是从随机向量中产生, 那么就应出自生成器的特殊网络结构。因此, 从随机向量造出图片, 要在造的过程中产生位置信息。 这个生成过程需符合以下两点原则。
(1) 保证信息在逐层计算中逐渐增多。
(2) 不损失位置信息, 并不断产生更细节的位置信息。
具体做法:
(1) 去掉一切会丢掉位置信息的结构, 如池化层。
(2)使用分数步进卷积层。
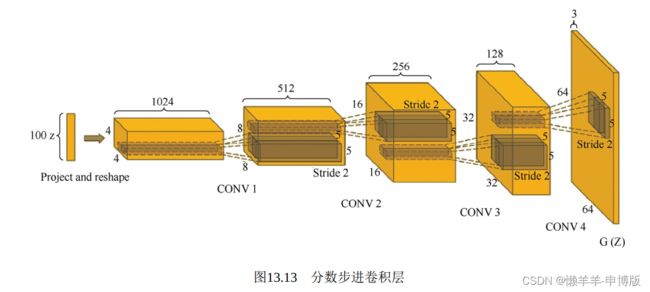
计算是升采样的过程, 逐步提供更多细节。将100维随机向量经过一层, 变换成一个4×4×1024的张量, 宽度和高度都为4, 虽然大小有限, 但是暗示了位置的存在, 接着经过层层变换, 高度和宽度不断扩大, 深度不断减小, 直至输出一个有宽度、 高度及RGB三通道的64×64×3图片。
( 3) 去掉最后的全连接层
越靠近图片输出端, 越要精心呵护宽高二维平面上的位置信息,反而在输入端可以增加一个全连接层。
( 4) 批量归一化和ReLU激活函数
生成模型越深, 越需要Batchnorm层, 否则训练不充分, 极易出现模型坍塌问题, 总生成相同的图片样本。 另外, 为了避免梯度饱和,让学习更稳定, 内部使用ReLU激活函数, 只在图片输出层用Tanh激活函数。
4.1.2 判别器
判别器鉴别生成图片和实际图片。 这是一个典型的图片分类任务, 但是又不同于一般的图片分类。 真品和赝品的区别, 往往是细节上的差异, 而不是宏观层面的语义差异。 判别器的多层卷积网络, 依然抛弃池化层, 将它替换为步长大于1的卷积层, 虽然也是一个降采样的过程, 但是没有池化层那样粗放。 判别器的最后一层不接全连接层, 扁平化处理后直接送给Sigmoid输出层, 最大限度地留住位置细节。 另外, 判别器的内部激活函数使用LReLU, 也是要最大限度地留住前层信息。 判别器也用到Batchnorm层。
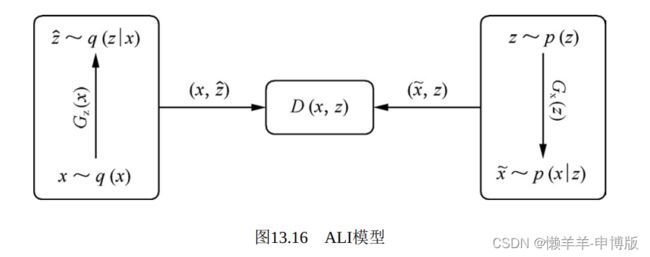
5ALI
任何一个观察数据x, 背后都有一个隐空间表示z。从概率的角度看, 编码是一个推断过程, 先从真实数据集采样一个样本x, 再由x推断z,有给定x下z的条件概率q(z|x); 解码是一个生成过程, 先从一个固定分布(如: 高斯分布N(0,I)) 出发, 采样一个随机信号 , 经过简单变换成为z, 再由z经过一系列复杂非线性变换生成x, 有给定z下x的条件概率p(x|z)。 将观察数据和其隐空间表示一起考虑, (x,z), 写出联合概率分布。 从推断的角度看, 联合概率q(x,z)=q(x)q(z|x), 其中q(x)为真实数据集上的经验数据分布, 可认为已知, 条件概率q(z|x)则要通过推断网络来表达; 从生成的角度看, p(x,z)=p(z)p(x|z), 其中p(z)是事先给定的, 如z~N(0,I), 条件概率p(x|z)则通过生成网络来表达。 让这两个联合概率分布q(x,z)和p(x,z)相互拟合。 当二者趋于一致时, 可以确定对应的边缘概率都相等, q(x)=p(x), q(z)=p(z), 对应的条件概率也都相等q(z|x)=p(z|x), q(x|z)=p(x|z)。
还有一个判别网络。 它的目标是区分来自生成网络和来自推断网络 ,