FIR滤波器的MATLAB与FPGA的设计实现
FIR滤波器的MATLAB与FPGA的设计实现
引言
数字滤波器是数字信号系统里面最常用、最重要、最基本的元件之一。有限脉冲响应(Finite Impulse Response,FIR)滤波器可以设计成任意幅频特性,同时保证精确,严格的线性相位特性。因此在电子通信、图像处理、模式识别等领域,FIR数字滤波器被广泛应用。本文主要通过以低通滤波器的MATLAB与FPGA的设计实现来介绍FIR滤波器的原理介绍,架构研究,设计实现等。
原理介绍
FIR滤波器的方程表达式为: y(n)=∑x(k)h(n-k) k=0,1…N-1;0≦n≦N-1;
其方程分解式为:y(n)=h(0)x(n)+h(1)x(n-1)+h(2)x(n-2)+…+h(k)x(n-k);
根据FIR滤波器的幅频特性可知,FIR滤波器为奇对称和偶对称两种形式。
例如当滤波器阶数为偶数n=3时,根据线性相位跟对称法则可得:h(0)=h(3),h(1)=h(2);
可得到方程式为:y(n)=h(0){x(n-1)+x(0)}+h(1){x(n-2)+x(1)};
当滤波器阶数为奇数n=4时,根据线性相位跟对称法则可得:h(0)=h(4),h(1)=h(3),h(2)独立一个;
可得到方程式为:y(n)=h(0){x(n-1)+x(0)}+h(1){x(n-2)+x(n-3)}+h(2)x(n-2);
故其系统函数为
![]()
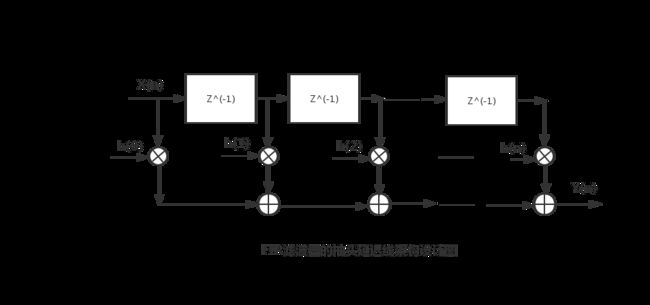
从其系统函数可以看得出FIR系统是线性时不变系统,只在原点上存在极点,这使得FIR系统具有全局稳定性。从FIR系统函数也可以看得出FIR滤波器其实是由一个抽头延迟线加法器和乘法器的集合构成的。每个乘法器的操作系数为FIR滤波器系数。因此这种抽头延迟线结构的架构实现图可如下所示:
MATLAB设计实现
在matlab里面设计数字滤波器既可以通过窗函数自己编写程序来设计FIR滤波器,也可以通过调用工具箱来设计FIR滤波器。通过编写程序来设计FIR滤波器比较普遍,滤波器的参数等改动也比较方便,与FPGA做联合功能仿真验证也方便。而直接调用工具箱就直接了当,较节省设计时间。本文将对两种方法进行介绍,不过本文设计采用的是凯塞窗函数来设计FIR滤波器。
窗函数设计法
利用窗函数法来设计FIR滤波器是设计FIR滤波器最简单,最普遍的方法,在MATLAB里面窗函数有海明(Hamming)窗,汉宁(Hanning)窗,凯塞(Kaiser)窗等,本文设计采用的是凯塞窗函数来设计FIR滤波器。通过最优算法来计算出过渡带,纹波等参数供给凯塞窗来计数出β值,以及滤波器的阶数。
凯塞窗函数的语法形式为:[n,wn,beta,ftype]=kaiserord(fc,mag,dev,fs)
其中各参数的意义介绍如下所述:
(1)fc及fs:fc是指过渡带的起始点和终点,fs指的是采样评率;
(2)mag:f指定了过渡带,向量a用于指定这些频率段的理想幅度值,例如a=[1 0]可以代指低通滤波为1,高频截止为0;
(3)dev:用于指定通带或阻带内的容许误差;
(4)n,wn:n是返回凯塞窗函数满足设计的最小阶数,wn是返回滤波器的截止频率点;
(5)beta:为凯塞窗函数计算得到的β值。
(6)ftype:返回设计滤波器的类型,low,hige等;
通过凯塞窗函数最终可以得到滤波器的最佳设计阶数n为多少,然后根据n来设计FIR滤波器,本文采用的是最优滤波器设计法,利用firpm函数根据最大误差最小准则来设计滤波器。
最优滤波器firpm函数的语法形式为:b_firpm = firpm(n,fpm,magpm)
其中各参数的意义介绍如下所述:
(1)n:为滤波器的设计阶数;
(2)fpm,magpm:指定滤波器的设计频率段对应的幅度值magpm;
(3)b_firpm:返回设计滤波器的系数h(n)。
到此为止设计FIR滤波器的matlab设计实现如下图所示,本文设计的是一个低通滤波器。

现在滤波器的系数b_firpm是可以求出来,但是注意是小数,在FPGA中实现还是比较麻烦还占用大量资源,所以在这里还进行了量化处理,对matlab数字滤波器的b_firpm进行14bit的量化处理(我在做量化的时候做了10,12,14bit的设计,发现14bit的滤波器效果最好)。

运行函数会发现生成了28阶的FIR滤波器系数如下所示,当n=27,滤波器阶数为28的时候,发现滤波器系数为对称相等的h(14)=h(15)=8191;
可验证到与前面的原理介绍是一致的。这样子后面在FPGA设计滤波器的时候可以用线性相位结构来设计。
![]()
运行函数,设计的低通滤波器性能如下图所示:
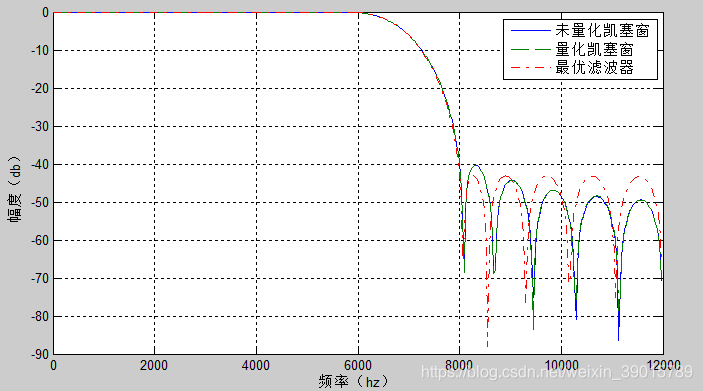
接下来生成高斯白噪声通过MATLAB设计的低通滤波器,来验证我们设计的低通滤波器性能如何,同时将生成的高斯白噪声生成数据文件txt供给后面的FPGA设计的低通滤波器做modelsim的功能仿真测试。生成白噪声的程序如下图所示,q_noise为高斯白噪声,filter_noise为滤波后噪声。

将生成的高斯白噪声生成数据文件txt供给后面的FPGA设计的低通滤波器做modelsim的功能仿真测试。
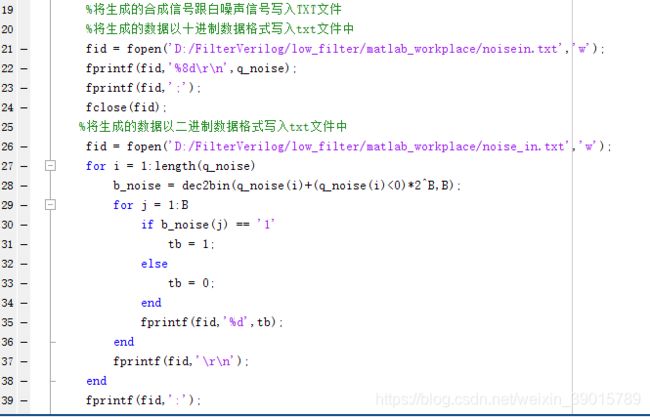
调用自己MATLAB设计的低通滤波器对高斯白噪声进行滤波,程序设计如下图所示:

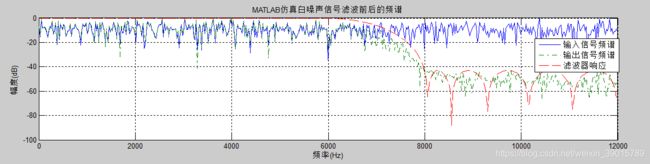
运行程序看设计的低通滤波器的性能如何,如下图所示,matlab设计的低通滤波器很完美的把高频率的数据进行截止滤波掉。在低频率的时候保持原高斯白噪声的输出状态。
tool工具箱设计法
在matlab的应用程序里面有一个filter design & analysis tool点进去即为快速设计滤波器的工具。操作界面如下图所示,较为简单不做详细介绍。
![]()
点analysis里面的filter coefficient即可出现设计滤波器的FIR滤波器系数,通过file-export可以把滤波器系数导出到workplace。
![]()
FPGA设计实现
在前面的原理介绍中可以得知,根据阶数的系数为对称相等的,于是抽头延迟线结构可以升级为线性相位优化结构来设计,具体我的架构设计图如下所示:
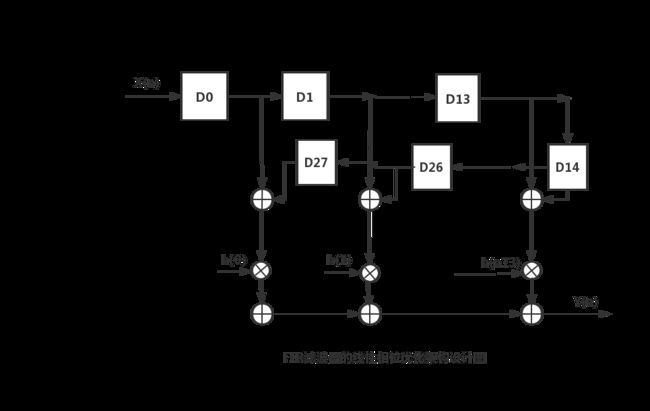
从上面的架构设计图可以看得出,FIR的设计大概可以分为三步分,数据流的移位延迟模块,系数和乘法器模块,累加和模块三大部分。
整体的端口设计介绍如下图所示:
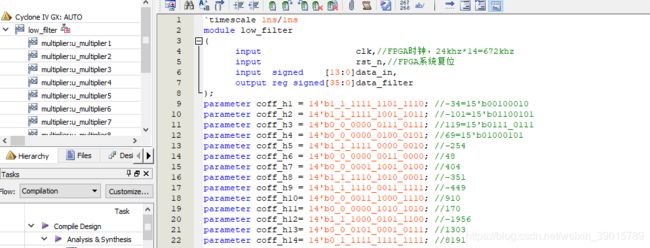
数据流的移位延迟模块
data_mem为28个14位宽的寄存器,进行数据流的采集跟移位保存。其设计如下图所示:
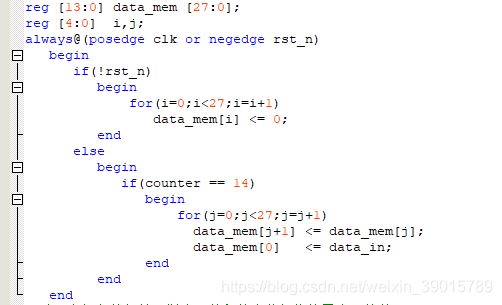
累加和的设计模块
这里的数据流有符号正负,所以在运算时为了不溢出,扩展一位,并用signed声明进行有符号的运算设计。
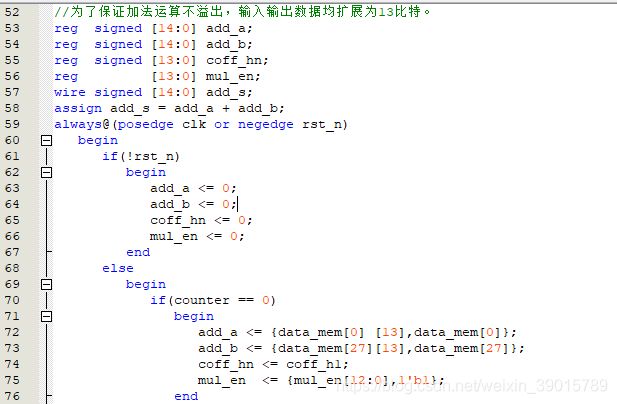
系数乘法器的设计模块
乘法器的设计端口介绍如下图所示:
![]()
乘法器的设计原理介绍如下图所示,具体的乘法设计可参考之前的博客章文:基于FPGA的乘法器原理介绍及设计实现,具体博文链接为:
https://blog.csdn.net/weixin_39015789/article/details/101430566
![]()
最后再将所有的乘积和进行累加便是对数据流进行低通滤波后的结果了。
MATLAB与FPGA的连仿验证
到现在为止,低通滤波器的FPGA设计实现也已经完毕了,接下来就是在modelsim里面读取matlab产生的高斯白噪声数据流,供给FPGA设计的FIR滤波器进行滤波计算,看两者的结果是否一模一样。
FPGA的textbench设计验证开始
读取高斯白噪声数据流
从外部txt文件(noise_in.txt)读入matlab产生的高斯白噪声数据流作为测试激励输入数据流。具体的设计如下所示:
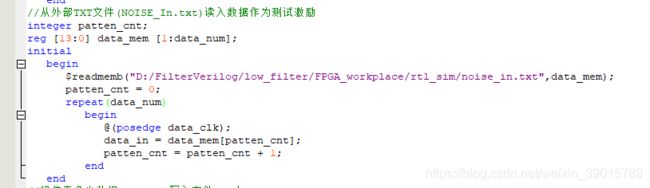
将FPGA滤波后的数据流读取到文件
将FPGA滤波后的数据流保存读取到文件,然后提供给matlab进行傅里叶变换,看FPGA设计的低通滤波器性能是如何的。
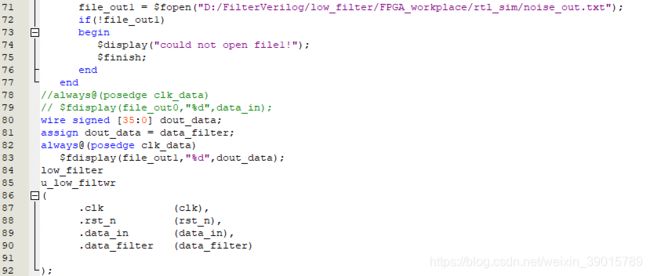
MATLAB与FPGA的连仿
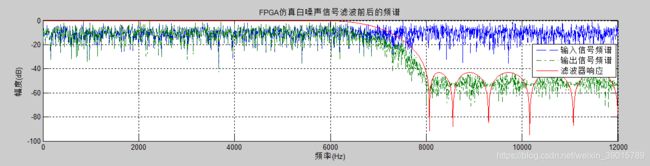
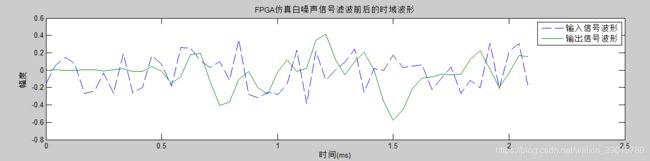
读取FPGA滤波后的数据,进行傅里叶变换,求高斯白噪声及滤波后信号的幅频响应,对比滤波前后的信号,查看滤波器的性能如何。

通过MATLAB将FPGA的滤波数据进行傅里叶变换的频谱滤波效果图如下所示,可以看到FPGA设计的低通滤波器在低频域的时候完美将高斯白噪声进行输出,在高频率的时候,对高斯白噪声进行滤波处理。效果性能与前面MATLAB设计的滤波器效果性能很是一致,滤波器的效果性能都很好。