OpenCV快速入门：像素操作和图像变换

前言

图像处理是计算机视觉领域中的核心内容之一，而像素操作和图像变换则是图像处理中不可或缺的基本操作。通过对像素的统计、加法操作、混合以及查找表等处理，我们能够灵活地调整图像的外观和内容。同时，图像变换则为我们提供了改变图像几何结构的手段，包括旋转、缩放、平移、翻转、仿射变换等多种操作。本篇博客将快速了解这些基础操作，并通过OpenCV展示它们的实际应用。

---

通过学习这些基础操作，读者将更好地理解图像处理的核心概念，为进一步深入学习计算机视觉和图像处理领域奠定坚实基础。

1. 像素操作

在图像处理中，像素是不可或缺的基本单元。OpenCV提供了丰富的像素操作函数，让我们能够灵活地访问和修改图像的像素值。

1.1 像素统计

像素统计是图像处理中常见的操作，可以帮助我们了解图像的整体特征。通过OpenCV，我们可以使用直方图来进行像素值的统计，进而分析图像的亮度分布。

以下面的郁金香为例。

import cv2
import numpy as np

# 读取图像
img = cv2.imread('tulips.jpg', 0)  # 以灰度模式读取图像

# 计算直方图
hist = cv2.calcHist([img], [0], None, [256], [0, 256])

# 创建一个画布，大小为 200x256，背景色为白色
hist_img = np.full((200, 256), 255, dtype=np.uint8)

# 归一化直方图，使其适应画布的高度
hist = cv2.normalize(hist, hist, 0, 200, cv2.NORM_MINMAX)

# 绘制直方图
for i in range(256):
    cv2.line(hist_img, (i, 200), (i, 200 - int(hist[i][0])), 0)

# 调整图像大小以匹配直方图
img_resized = cv2.resize(img, (256, 200))
# 将图像与直方图横向拼接
result = cv2.hconcat([img_resized, hist_img])
# 显示结果
cv2.imshow('Image and Histogram', result)
cv2.waitKey(0)
cv2.destroyAllWindows()

直方图是对图像中像素值分布的图形化表示。通过直方图，我们可以了解图像中像素值的分布情况，从而揭示图像的亮度、对比度等特征。以下是直方图中一些常见的解释要点：

1. X轴和Y轴：

   • X轴（横轴）： 表示图像的像素值。通常，0代表黑色，255代表白色。
   • Y轴（纵轴）： 表示对应像素值的像素数量或频率。

2. 峰值和谷值：

   • 峰值： 直方图中的高峰表示图像中有大量具有相同像素值的区域。这可能对应于图像中的主要物体或背景。
   • 谷值： 直方图中的低谷表示图像中像素值稀疏的区域，可能是物体的边缘或其他低纹理区域。

3. 分布形状：

   • 对称分布： 如果直方图在中间值附近对称，则图像可能具有均匀的亮度分布。
   • 偏斜分布： 如果直方图在一个方向上延伸，则图像可能具有明显的亮度或对比度偏移。

4. 峰的位置和宽度：

   • 峰的位置： 峰值的位置表示图像中主要的亮度级别。例如，峰值在低像素值端，可能表示图像主要是暗的。
   • 峰的宽度： 宽峰可能表示亮度分布较为均匀，而窄峰可能表示亮度分布集中在某一范围内。

5. 直方图均衡化的效果：

   • 直方图均衡化是一种通过调整图像的像素值分布来增强对比度的方法。均衡化后的直方图应该更加平均，使得图像更具有视觉吸引力。

在直方图中，可以看到高峰和低谷，以及整体的分布形状。这有助于更好地理解图像的特性，为进一步的图像处理提供了重要的信息。

1.2 两个图像之间的操作

在图像处理中，对两个图像进行操作是一种常见的需求，这可以包括加法、减法、混合等。OpenCV提供了一系列的函数来执行这些操作，其中 cv2.add() 是用于执行图像加法的函数。

1.2.1 图像加法操作

图像加法是将两幅图像的对应像素值相加，得到一个新的图像。这种操作常用于图像的亮度调整和合成。具体而言，对于两个图像 A 和 B，其加法操作可以表示为：

$$\text{result}(x,y)=\text{clip}(\text{A}(x,y)+\text{B}(x,y))$$

其中，clip 表示将结果限制在合理的范围内（通常是 0 到 255，对于8位图像而言）。

OpenCV中的图像加法

使用 cv2.add() 函数，我们可以轻松地执行图像加法。以下是一个简单的例子：
tulips1.jpg

tulips2.jpg

import cv2

# 读取两张图像
img1 = cv2.imread('tulips1.jpg')
img2 = cv2.imread('tulips2.jpg')

# 确保两张图像具有相同的尺寸
img2_resized = cv2.resize(img2, (img1.shape[1], img1.shape[0]))

# 图像加法
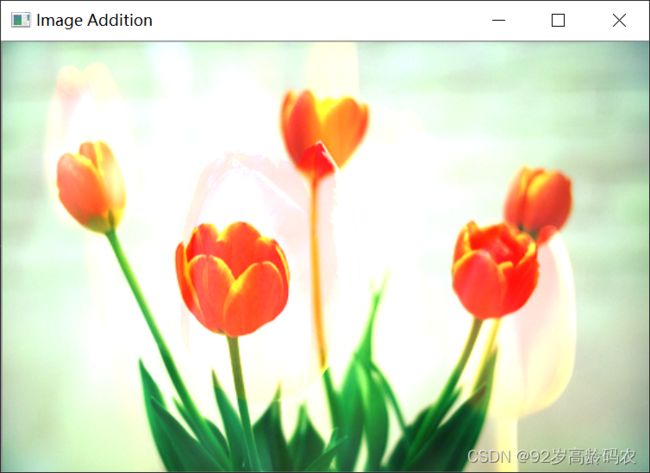
result = cv2.add(img1, img2_resized)

# 显示结果
cv2.imshow('Image Addition', result)
cv2.waitKey(0)
cv2.destroyAllWindows()

在这个例子中，cv2.add() 函数将两张图像的对应像素值相加，生成了一个新的图像 result。通过这个操作，图像的亮度得到了增强。

1.2.3 图像加权混合

除了简单的图像加法，OpenCV还支持图像的加权混合。这种混合是通过为每个图像分配一个权重，然后将它们相加得到的。具体而言，对于两个图像 A 和 B，其加权混合操作可以表示为：

$$\text{result}=\text{A}\cdot \alpha +\text{B}\cdot \beta +\text{gamma}$$

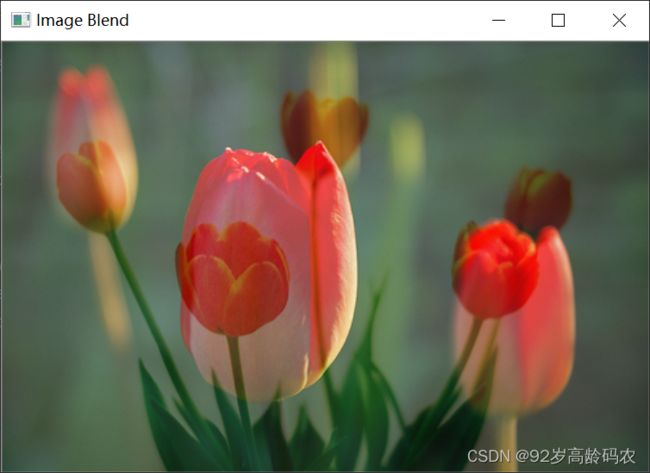
在OpenCV中，这可以通过 cv2.addWeighted() 函数实现：

import cv2

# 读取两张图像
img1 = cv2.imread('tulips1.jpg')
img2 = cv2.imread('tulips2.jpg')

# 确保两张图像具有相同的尺寸
img2_resized = cv2.resize(img2, (img1.shape[1], img1.shape[0]))

# 设置加权混合的权重
alpha = 0.7
beta = 0.3
gamma = 0

# 图像加权混合
result = cv2.addWeighted(img1, alpha, img2_resized, beta, gamma)

# 显示结果
cv2.imshow('Image Blend', result)
cv2.waitKey(0)
cv2.destroyAllWindows()

在这个例子中，cv2.addWeighted() 函数接受五个参数：

• img1：第一张图像
• alpha：第一张图像的权重
• img2：第二张图像
• beta：第二张图像的权重
• gamma：加法的常数项

通过调整 alpha 和 beta 的值，可以控制两张图像在混合中的权重。通常情况下，alpha + beta 应该等于 1。
gamma 用于调整亮度。

通过这种方式，可以在图像中进行平滑的混合，从而创造出一些特殊的效果。

1.3 二值化

在图像处理中，二值化是一种常见的操作，其目的是将图像转换为只包含两种像素值的形式，通常是黑和白。这种操作可以用于物体检测、图像分割、文本识别等应用场景。

OpenCV提供了多种二值化方法，其中最简单的是使用 cv2.threshold() 函数。

import cv2

# 读取图像
img = cv2.imread('tulips1.jpg', 0)  # 以灰度模式读取图像

# 二值化
ret, binary_img = cv2.threshold(img, 60, 255, cv2.THRESH_BINARY)

# 显示结果
cv2.imshow('Binary Image', binary_img)
cv2.waitKey(0)
cv2.destroyAllWindows()

cv2.threshold() 函数用于对输入图像进行阈值处理。该函数有四个主要的参数：

• 输入图像 (img)： 要进行二值化处理的图像。
• 阈值 (thresh)： 阈值是一个用于将像素分为两类的数值。超过阈值的像素被置为一个值，未超过的像素被置为另一个值。
• 最大值 (maxval)： 超过阈值的像素被赋予的值。在二值化中，通常将其设为最大像素值。
• 二值化类型 (type)： 二值化的类型，常见的有 cv2.THRESH_BINARY、cv2.THRESH_BINARY_INV 等。

代码中，cv2.threshold(img, 60, 255, cv2.THRESH_BINARY): 对灰度图像进行阈值处理。像素值大于60的被置为255（白色），小于等于60的被置为0（黑色）。这里使用的是二进制阈值化，即 cv2.THRESH_BINARY。

通过这个简单的二值化操作，图像中的信息被转换成了黑白两种像素值，使得后续的处理更加方便。

1.4 LUT（查找表）

在图像处理中，查找表（Look-Up Table，LUT）是一种通过预先定义的映射关系对图像进行像素值映射的方法。OpenCV提供了 cv2.LUT() 函数，使得对图像的像素值进行非常灵活的映射成为可能。

1.4.1 查找表原理

查找表的原理是通过预先定义好的映射表，将输入图像的每个像素值映射到输出图像的对应像素值。这种操作常常用于对图像进行颜色校正、增强对比度、调整亮度等。

在OpenCV中，查找表是一个三维数组，其中每个通道都有一个单独的映射表。通过对查找表的预处理，可以实现各种各样的图像处理效果。

1.4.2 代码演示

以下是OpenCV的代码演示：

import cv2
import numpy as np

# 读取彩色图像
img = cv2.imread('tulips1.jpg')

# 获取图像的高度和宽度
height, width, channels = img.shape

# 创建查找表
lut = np.zeros((256, 1, 3), dtype=np.uint8)

# 处理红色通道
for i in range(256):
    # 小于100的值设为100，大于200的值设为200，其余的设为150
    lut[i, 0, 0] = max(min(200, i), 100)

# 处理绿色通道
for i in range(256):
    # 翻转颜色
    lut[i, 0, 1] = 255 - i

# 处理蓝色通道，保持不变
for i in range(256):
    lut[i, 0, 2] = i

# 应用查找表
result = cv2.LUT(img, lut)

# 显示原始图像和处理后的图像
cv2.imshow('Color Transformation', np.hstack([img, result]))
cv2.waitKey(0)
cv2.destroyAllWindows()

• cv2.LUT(img, lut): 使用 cv2.LUT() 函数应用查找表，将输入图像 img 的每个像素值通过查找表进行映射，生成处理后的图像 result。

• np.hstack([img, result]): 使用 np.hstack() 函数将原始图像和处理后的图像水平拼接，以便更直观地比较两者的效果。

通过定义不同的查找表，可以实现对图像的多种处理效果，使图像处理更加灵活和可控。

2 图像变换

通过对图像进行变换，我们可以实现图像的旋转、缩放、平移等操作，从而达到不同的视觉效果和分析目的。在OpenCV中，图像变换操作具有灵活性和高效性，本章节将介绍一些基础的图像变换操作。

2.1 旋转操作

2.1.1 旋转的基本原理

旋转操作是将图像绕着其中心点旋转一定的角度。这个旋转的过程可以通过一个矩阵来表示，即旋转矩阵。对于2D图像，旋转矩阵的表达式为：

$$R=\left[\begin{array}{cc}\cos (\theta )& -\sin (\theta )\\ \sin (\theta )& \cos (\theta )\end{array}\right]$$

其中，$\theta$ 是旋转的角度。对于图像旋转，我们通常使用 cv2.getRotationMatrix2D 函数来获取旋转矩阵。
在常规的坐标系中，逆时针旋转被认为是正方向。因此，正的旋转角度 $\theta$ 表示逆时针旋转，而负的旋转角度表示顺时针旋转。

2.1.2 代码实现

import cv2

# 读取图像
img = cv2.imread('tulips1.jpg')

# 获取图像的高度和宽度
height, width = img.shape[:2]

# 定义旋转角度
angle = 45

# 计算旋转矩阵
rotation_matrix = cv2.getRotationMatrix2D((width/2, height/2), angle, 1)

# 进行图像旋转
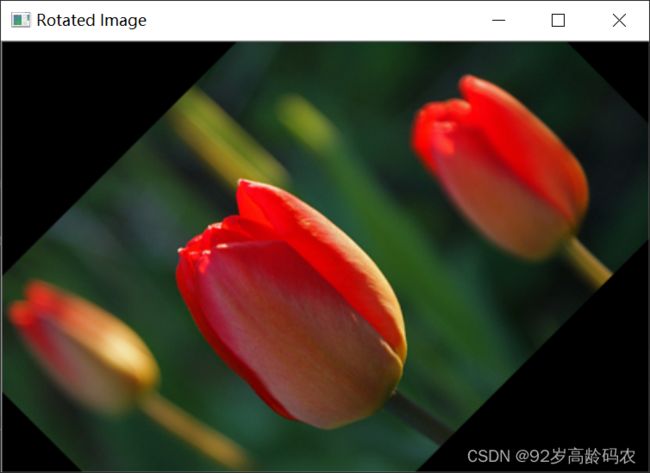
rotated_img = cv2.warpAffine(img, rotation_matrix, (width, height))

# 显示旋转后的图像
cv2.imshow('Rotated Image', rotated_img)
cv2.waitKey(0)
cv2.destroyAllWindows()

在这段代码中，cv2.getRotationMatrix2D 函数计算了一个旋转矩阵，然后通过 cv2.warpAffine 函数进行了图像的实际旋转操作。通过改变 angle 的值，我们可以实现不同角度的图像旋转，从而达到不同的视觉效果。

cv2.getRotationMatrix2D 函数中的 angle 参数表示逆时针旋转的角度。如果希望进行顺时针旋转，只需将 angle 设为负值即可。例如，若要顺时针旋转 45 度，可以将 angle = -45。

cv2.getRotationMatrix2D
是OpenCV中用于获取旋转矩阵的函数，它用于构建一个二维旋转变换矩阵。该函数的语法如下：

python cv2.getRotationMatrix2D(center, angle, scale)

其中：

• center 是旋转的中心点坐标，通常为图像的中心 (width/2, height/2)。
• angle 是旋转角度，以逆时针方向为正。
• scale 是可选的缩放因子，默认为1。

该函数返回一个2x3的矩阵，即旋转矩阵。这个矩阵可以用于后续的图像旋转操作。

在旋转矩阵中，前两列是旋转的两个基向量，第三列是中心点的坐标。形式如下：

$$R=\left[\begin{array}{ccc}\alpha & \beta & (1-\alpha )\cdot {\text{center}}_x-\beta \cdot {\text{center}}_y\\ -\beta & \alpha & \beta \cdot {\text{center}}_x+(1-\alpha )\cdot {\text{center}}_y\end{array}\right]$$

其中，$\alpha =\text{scale}\cdot \cos (\text{angle})$且 $\beta =\text{scale}\cdot \sin (\text{angle})$。

这个矩阵表示了旋转和缩放的组合变换。这个变换可以通过 cv2.warpAffine 函数应用到图像上，实现旋转和缩放的效果。

2.2 缩放操作

缩放是调整图像大小的基本操作，通过改变图像的宽度和高度，我们可以实现图像的缩小或放大。在图像处理中，缩放操作经常用于调整图像大小以适应不同的显示需求或分析环境。

缩放操作的基本原理是通过对图像的像素进行重新排列，从而改变图像的尺寸。对于缩小操作，通常使用图像插值技术来估算新的像素值；而对于放大操作，则使用插值来填充新的像素。

在OpenCV中，可以使用 cv2.resize 函数实现图像的缩放。

import cv2
import numpy as np

# 读取图像
img = cv2.imread('tulips1.jpg')

# 定义缩放比例
scale_percent = 50  # 缩放到原图的50%

# 计算缩放后的宽度和高度
width = int(img.shape[1] * scale_percent / 100)
height = int(img.shape[0] * scale_percent / 100)

# 进行图像缩放
resized_img = cv2.resize(img, (width, height))

# 创建黑色背景图像
black_background = np.zeros((max(height, img.shape[0]), max(width, img.shape[1]), 3), dtype=np.uint8)

# 将缩放后的图像放置在黑色背景上
black_background[:resized_img.shape[0], :resized_img.shape[1], :] = resized_img

# 显示原始图像、缩放后的图像
result = cv2.hconcat([img, black_background])
cv2.imshow('Resized Image', result)
cv2.waitKey(0)
cv2.destroyAllWindows()

cv2.resize函数有以下参数：

cv2.resize(src, dsize[, dst[, fx[, fy[, interpolation]]]])

• src: 原始图像。
• dsize: 输出图像的大小，可以是元组 (width, height) 或者单个值。
• dst: 可选参数，输出图像。
• fx: 沿水平轴的缩放比例。
• fy: 沿垂直轴的缩放比例。
• interpolation: 插值方法，用于确定新像素值。默认为 cv2.INTER_LINEAR。

在上面的示例代码中，我们使用了 cv2.resize(img, (width, height))，其中 img 是原始图像，(width, height) 是输出图像的大小。我们没有显式设置 fx 和 fy，因此默认情况下它们都为1，表示沿着水平和垂直方向上的缩放因子都为1。这样的设置等效于等比例缩放。

cv2.resize 函数中的 interpolation 参数用于指定图像缩放时的插值方法。以下是常用的插值方法选项：

1. cv2.INTER_NEAREST: 最近邻插值。计算新像素值时，选择最近的已知像素值。

2. cv2.INTER_LINEAR: 线性插值。计算新像素值时，使用相邻的4个像素的加权平均。

3. cv2.INTER_CUBIC: 三次样条插值。计算新像素值时，使用相邻的16个像素的加权平均，产生更平滑的效果。

4. cv2.INTER_AREA: 区域插值。计算新像素值时，使用像素区域的像素值的平均。

5. cv2.INTER_LANCZOS4: Lanczos窗口插值。计算新像素值时，使用Lanczos窗口函数的加权平均。

在实际应用中，选择合适的插值方法取决于图像的内容和应用场景。例如，对于图像放大，通常使用 cv2.INTER_LINEAR 或
cv2.INTER_CUBIC 来保持图像质量。如果需要快速的缩小操作，可以考虑使用 cv2.INTER_NEAREST。

2.3 平移操作

平移是将图像沿着x和y轴移动的操作，通过改变图像的位置，我们可以实现图像的平移。在图像处理中，平移操作常用于调整图像在画布上的位置，以便进一步的处理或显示。在OpenCV中，可以使用 cv2.warpAffine 函数实现图像的平移。

2.3.1 平移操作原理

平移操作的原理是通过构建一个平移矩阵，将图像中的每个像素移动到新的位置。平移矩阵的形式如下：

$$M=\left[\begin{array}{ccc}1& 0& \text{tx}\\ 0& 1& \text{ty}\end{array}\right]$$

其中，$\text{tx}$ 是沿x轴的平移量，$\text{ty}$ 是沿y轴的平移量。通过 cv2.warpAffine 函数应用这个平移矩阵，即可完成图像的平移操作。

2.3.2 代码实现

以下是一个平移操作的示例代码，通过构建平移矩阵将原始图像沿x轴平移50个像素，沿y轴平移30个像素：

import cv2
import numpy as np

# 读取图像
img = cv2.imread('tulips1.jpg')

# 定义平移矩阵
translation_matrix = np.float32([[1, 0, 50], [0, 1, 30]])  # 沿x轴平移50个像素，沿y轴平移30个像素

# 进行图像平移
translated_img = cv2.warpAffine(img, translation_matrix, (img.shape[1], img.shape[0]))

# 显示平移后的图像
cv2.imshow('Translated Image', translated_img)
cv2.waitKey(0)
cv2.destroyAllWindows()

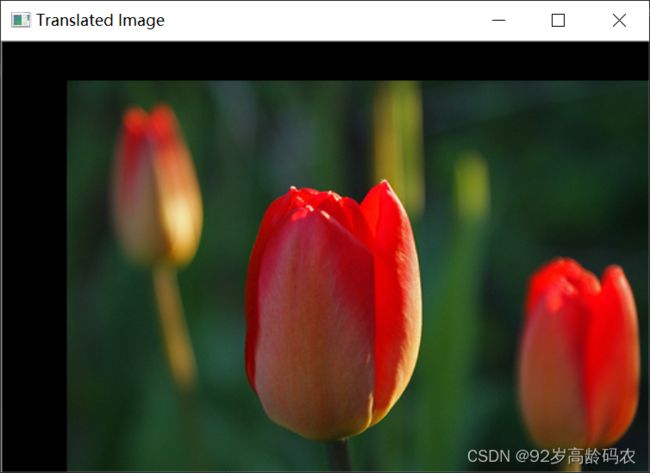
在这个例子中，我们通过 np.float32 创建了一个平移矩阵 translation_matrix，然后使用 cv2.warpAffine 函数将原始图像进行平移。最终，我们显示了原始图像和平移后的图像，通过调整平移矩阵中的参数，可以实现不同方向和距离的平移效果。

2.4 翻转操作

翻转操作通过改变图像的方向，我们可以获得不同的视觉效果。本章将介绍如何使用OpenCV进行图像的水平翻转、垂直翻转以及同时进行水平和垂直翻转的操作。

2.4.1 水平翻转

水平翻转是将图像沿着垂直中轴线进行翻转，即左侧变为右侧，右侧变为左侧。在OpenCV中，可以使用 cv2.flip 函数来实现水平翻转。

import cv2

# 读取图像
img = cv2.imread('tulips1.jpg')

# 进行水平翻转
horizontal_flip = cv2.flip(img, 1)

# 显示原始图像和水平翻转后的图像
cv2.imshow('Horizontal Flip', cv2.hconcat([img, horizontal_flip]))
cv2.waitKey(0)
cv2.destroyAllWindows()

2.4.2 垂直翻转

垂直翻转是将图像沿着水平中轴线进行翻转，即上方变为下方，下方变为上方。同样地，在OpenCV中，可以使用 cv2.flip 函数来实现垂直翻转。

import cv2

# 读取图像
img = cv2.imread('tulips1.jpg')

# 进行垂直翻转
vertical_flip = cv2.flip(img, 0)

# 显示原始图像和垂直翻转后的图像
cv2.imshow('Vertical Flip', cv2.vconcat([img, vertical_flip]))
cv2.waitKey(0)
cv2.destroyAllWindows()

2.4.3 同时进行水平和垂直翻转

同时进行水平和垂直翻转是将图像在水平和垂直方向上同时进行翻转，即左上角变为右下角，右下角变为左上角。在OpenCV中，可以使用 cv2.flip 函数的参数来实现同时进行水平和垂直翻转。

import cv2

# 读取图像
img = cv2.imread('tulips1.jpg')

# 同时进行水平和垂直翻转
both_flip = cv2.flip(img, -1)

# 显示原始图像和同时进行水平和垂直翻转后的图像
cv2.imshow('Both Flip', cv2.hconcat([img, both_flip]))
cv2.waitKey(0)
cv2.destroyAllWindows()

通过这三种翻转操作，我们可以轻松地改变图像的方向，适应不同的显示或处理需求。在实际应用中，翻转操作经常用于数据增强、图像处理等场景，为图像处理任务提供更多的变化和选择。

2.5 仿射变换

通过仿射变换，我们可以实现图像的平移、旋转、缩放和剪裁等操作。在OpenCV中，仿射变换是一项强大而灵活的图像处理技术，本章将介绍如何使用OpenCV进行仿射变换。

2.5.1 仿射变换原理

仿射变换是通过线性变换和平移组合而成的一种几何变换。在二维图像中，仿射变换可以表示为：

$$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{cc}a& b\\ c& d\end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]+\left[\begin{array}{c}tx\\ ty\end{array}\right]$$

其中，$\left[\begin{array}{c}x\\ y\end{array}\right]$ 是原始图像上的坐标，$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right]$ 是变换后图像上的坐标，$\left[\begin{array}{cc}a& b\\ c& d\end{array}\right]$ 是线性变换矩阵，$\left[\begin{array}{c}tx\\ ty\end{array}\right]$ 是平移向量。

2.5.2 构建仿射矩阵

在OpenCV中，可以使用 cv2.getAffineTransform 函数根据三个对应的点构建仿射矩阵。假设有三个对应的点 $(x_1,y_1)\leftrightarrow (x_1^{\prime },y_1^{\prime })$，$(x_2,y_2)\leftrightarrow (x_2^{\prime },y_2^{\prime })$，$(x_3,y_3)\leftrightarrow (x_3^{\prime },y_3^{\prime })$，则可以通过以下方式构建仿射矩阵：

import cv2
import numpy as np

# 原始图像上的三个对应点
pts_original = np.float32([[50, 50], [200, 50], [50, 200]])

# 变换后的图像上的三个对应点
pts_transformed = np.float32([[10, 100], [200, 50], [100, 250]])

# 构建仿射矩阵
affine_matrix = cv2.getAffineTransform(pts_original, pts_transformed)

2.5.3 进行仿射变换

使用得到的仿射矩阵，可以通过 cv2.warpAffine 函数进行仿射变换。以下是一个示例，将原始图像进行仿射变换：

import cv2
import numpy as np

# 读取图像
img = cv2.imread('tulips1.jpg')

# 原始图像上的三个对应点
pts_original = np.float32([[50, 50], [200, 50], [50, 200]])

# 变换后的图像上的三个对应点
pts_transformed = np.float32([[10, 100], [200, 50], [100, 250]])

# 构建仿射矩阵
affine_matrix = cv2.getAffineTransform(pts_original, pts_transformed)

# 进行仿射变换
affine_img = cv2.warpAffine(img, affine_matrix, (img.shape[1], img.shape[0]))

# 显示仿射变换后的图像
cv2.imshow('Affine Transformation', affine_img)
cv2.waitKey(0)
cv2.destroyAllWindows()

通过调整 pts_original 和 pts_transformed 中的对应点，可以实现不同的仿射变换效果。这为图像的几何调整提供了一种强大的工具。

2.6 投射变换

投射变换是图像处理中的一种重要技术，它涉及将三维场景映射到二维图像上。在OpenCV中，投射变换常用于摄像机标定、虚拟增强现实等应用中。本章将介绍投射变换的基本原理以及如何在OpenCV中实现投射变换。

2.6.1 投射变换基本原理

投射变换涉及将三维空间中的点映射到二维图像上。这一映射过程通常由一个投射矩阵来描述。对于透视投射，投射矩阵可以表示为：

s [ f x 0 c x 0 f y c y 0 0 1 ] [ r 11 r 12 r 13 t x r 21 r 22 r 23 t y r 31 r 32 r 33 t z ] s \begin{bmatrix} f_x & 0 & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} r_{11} & r_{12} & r_{13} & t_x \\ r_{21} & r_{22} & r_{23} & t_y \\ r_{31} & r_{32} & r_{33} & t_z \end{bmatrix} s ​fx​00​0fy​0​cx​cy​1​ ​ ​r11​r21​r31​​r12​r22​r32​​r13​r23​r33​​tx​ty​tz​​ ​

其中，$s$ 是尺度因子，$f_x$ 和 $f_y$ 是焦距，$(c_x,c_y)$ 是主点，$(t_x,t_y,t_z)$ 是平移向量，$r_{ij}$ 是旋转矩阵的元素。

2.6.2 透视投射变换代码实现

在OpenCV中，可以使用 cv2.getPerspectiveTransform 函数来获取透视投射变换矩阵。以下是一个简单的示例，实现透视投射变换：

import cv2
import numpy as np

# 读取图像
img = cv2.imread('tulips1.jpg')

# 原始图像上的四个对应点
pts_original = np.float32([[50, 50], [200, 50], [50, 200], [200, 200]])

# 变换后的图像上的四个对应点
pts_transformed = np.float32([[0, 0], [300, 100], [100, 300], [100, 100]])

# 获取透视投射变换矩阵
perspective_matrix = cv2.getPerspectiveTransform(pts_original, pts_transformed)

# 进行透视投射变换
perspective_img = cv2.warpPerspective(img, perspective_matrix, (img.shape[1], img.shape[0]))

# 显示原始图像和透视投射变换后的图像
cv2.imshow('Perspective Transformation', cv2.hconcat([img, perspective_img]))
cv2.waitKey(0)
cv2.destroyAllWindows()

通过调整 pts_original 和 pts_transformed 中的对应点，可以实现不同的透视投射效果。这一技术在计算机视觉和图像处理中具有广泛的应用，尤其是在图像校正和三维场景还原中。

2.7 极坐标变换

极坐标变换是一种将笛卡尔坐标系下的图像转换为极坐标系的技术。这种变换方式在某些图像处理和计算机视觉任务中非常有用，例如在边缘检测、图像滤波和特征提取等方面。本章将介绍极坐标变换的基本原理以及在OpenCV中如何实现这种变换。

2.7.1 极坐标变换基本原理

极坐标变换将图像从直角坐标系转换为极坐标系。在直角坐标系中，以$O(0,0)$为原点，像素点的坐标表示为 $(x,y)$，而在极坐标系中，坐标表示为 $(\rho ,\theta )$，其中 $\rho$ 是极径，表示点到原点的距离，$\theta$ 是极角，表示点相对于正 x 轴的角度。

变换过程可以用以下公式表示：

1. 已知 $(x,y)$，则：
   $$\{\begin{array}{rl}\rho & =\sqrt{x^2+y^2}\\ \theta & =\arctan \left(\frac{y}{x}\right)\end{array}$$

2. 已知$(\rho ,\theta )$，则：
   $$\{\begin{array}{rl}x& =\rho \cdot \cos (\theta )\\ y& =\rho \cdot \sin (\theta )\end{array}$$

2.7.2 极坐标变换代码实现

示例图片：color_plate.jpg

以下是一个简单的代码示例：

import cv2
import numpy as np
import math
# 读取图像
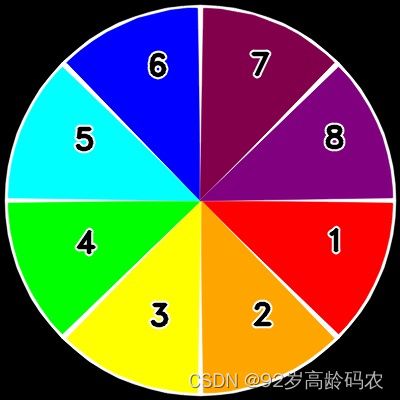
img = cv2.imread('color_plate.jpg')

# 创建一个黑色的图像
image_size = img.shape[0]

# 圆心坐标
center = (image_size // 2, image_size // 2)
# 圆的半径
radius = image_size // 2

# PAI值
PI = math.pi
# 极坐标转换后的图像的宽（圆形的周长）
line_width = int(2 * radius * PI)

# 开始极坐标变换
# 建立展开后的图像
polar_image = np.zeros((radius, line_width, 3), dtype=np.uint8)
# 按照圆的极坐标赋值
for row in range(polar_image.shape[0]):
    for col in range(polar_image.shape[1]):
        # 逆时针转动theta角
        theta = - col / line_width * PI * 2
        # 数组下标都从0开始，因此计算结果都要-1，防止越界
        x = int(center[0] + row * math.cos(theta)) - 1
        y = int(center[1] + row * math.sin(theta)) - 1

        # 赋值
        polar_image[row, col, :] = img[y, x, :]
polar_image = cv2.rotate(polar_image, cv2.ROTATE_90_CLOCKWISE)
# 展示结果
cv2.imshow("Polar Image", polar_image)
cv2.waitKey()
cv2.destroyAllWindows()

极坐标变换的基本原理在上述代码中得到了清晰的体现。首先，通过极坐标到直角坐标的转换公式，计算了展开后每个像素点在原图中的坐标位置，然后将对应位置的像素值赋给展开后的图像。这样就完成了从圆形图像到线形图像的转换。

代码实现解读：

1. 图像准备： 读取原始图像并创建一个黑色的图像用于存储极坐标变换后的结果。

2. 参数设置： 定义圆心坐标、半径、以及一些常数如 $\pi$。

3. 展开图像： 使用两层循环，对展开后的图像的每个像素点进行计算。逆时针旋转角度 $\theta$，然后计算对应的极坐标，并根据极坐标找到原图像中对应的像素位置。

4. 图像赋值： 将原图像中对应位置的像素值赋给展开后的图像。

5. 显示结果： 最后，通过旋转函数 cv2.rotate 将图像旋转90度方便显示。

2.7.3 极坐标逆变换

为了还原回圆形，我们需要反向操作，将极坐标图像重新映射到直角坐标系。
彩色板和极坐标转换全部代码演示：

import cv2
import numpy as np
import math

# 创建一个黑色的图像
image_size = 400
image = np.zeros((image_size, image_size, 3), dtype=np.uint8)

# 圆心坐标
center = (image_size // 2, image_size // 2)
# 圆的半径
radius = image_size // 2 - 5

# 分成八份
num_sectors = 8
angle_step = 360 // num_sectors

# 九种颜色（包括新颜色）
colors = [
    (0, 0, 255),  # 红
    (0, 165, 255),  # 橙
    (0, 255, 255),  # 黄
    (0, 255, 0),  # 绿
    (255, 255, 0),  # 青
    (255, 0, 0),  # 蓝
    (75, 0, 130),  # 靛
    (128, 0, 128),  # 紫
]

# 画扇形
for i in range(num_sectors):
    start_angle = i * angle_step
    end_angle = (i + 1) * angle_step
    color = colors[i]

    # 画白色扇形
    cv2.ellipse(image, center, (radius, radius), 0, start_angle, end_angle, (255, 255, 255), -1, lineType=cv2.LINE_AA)
    # 画彩色扇形
    cv2.ellipse(image, center, (radius - 3, radius - 3), 0, start_angle + 1, end_angle - 1, color, -1,
                lineType=cv2.LINE_AA)

    # 计算扇形中央坐标
    mid_angle = (start_angle + end_angle) // 2
    mid_x = int(center[0] + (radius - 60) * np.cos(np.radians(mid_angle)))
    mid_y = int(center[1] + (radius - 60) * np.sin(np.radians(mid_angle)))
    # 添加数字
    cv2.putText(image, str(i + 1), (mid_x, mid_y), cv2.FONT_HERSHEY_DUPLEX, 1, (255, 255, 255), 6, cv2.LINE_AA)
    cv2.putText(image, str(i + 1), (mid_x, mid_y), cv2.FONT_HERSHEY_DUPLEX, 1, (0, 0, 0), 2, cv2.LINE_AA)

# PAI值
PI = math.pi
# 极坐标转换后的图像的宽（圆形的周长）
line_width = int(2 * radius * PI)

# 开始极坐标变换
# 建立展开后的图像
polar_image = np.zeros((radius, line_width, 3), dtype=np.uint8)
# 按照圆的极坐标赋值
for row in range(polar_image.shape[0]):
    for col in range(polar_image.shape[1]):
        # 逆时针转动theta角
        theta = - col / line_width * PI * 2
        # 数组下标都从0开始，因此计算结果都要-1，防止越界
        x = int(center[0] + row * math.cos(theta)) - 1
        y = int(center[1] + row * math.sin(theta)) - 1

        # 赋值
        polar_image[row, col, :] = image[y, x, :]

# 还原极坐标图像
restored_image = np.zeros_like(image)
for row in range(polar_image.shape[0]):
    for col in range(polar_image.shape[1]):
        # 逆时针转动 theta 角
        theta = -col / polar_image.shape[1] * PI * 2
        # 计算在直角坐标系中的坐标
        x = int(center[0] + row * math.cos(theta))
        y = int(center[1] + row * math.sin(theta))
        # 赋值
        restored_image[y, x, :] = polar_image[row, col, :]

# 展示结果
polar_image = cv2.rotate(polar_image, cv2.ROTATE_90_CLOCKWISE)
polar_image = cv2.resize(polar_image, (int(2 * radius * image_size / line_width), image_size))
cv2.imshow("Polar and Restored Image", cv2.hconcat([image, polar_image, restored_image]))
cv2.waitKey()
cv2.destroyAllWindows()

---

总结

这篇博客中，我们了解了像素操作和图像变换的多个方面。

• 首先，通过像素统计、图像加法、混合以及二值化等操作，我们展示了如何灵活处理图像像素以达到不同的效果。查找表作为一种高效的像素值映射方式，也为图像处理提供了便捷的工具。

• 接着，我们深入学习了图像变换的多个方面，包括旋转、缩放、平移、翻转、仿射变换以及投射变换。每个操作都有其独特的原理和实现方式，而OpenCV提供的函数使得这些操作变得更加简单高效。

• 特别地，我们探讨了极坐标变换，这是一种将图像从直角坐标系转换为极坐标系的技术。通过详细讲解基本原理和代码实现，我们展示了极坐标变换在图像处理中的潜在应用。