动态规划之最长不下降子序列
一、概念明确
先来看一串数字:(20,17,19,22,4,7,10,12,5,2,13)
1.序列:像以上排成一列的数字,我们叫它序列,其中每个数字,可以被称为一个元素。
2.子序列:将序列中的部分元素或者全部元素取出后构成的一个新序列,我们称为子序列。
例:将元素 17,22,6,7 取出来构成一个新序列 (17,22,6,7),那么它就是一个子序列
注意:子序列是有序的,不能将后面的元素写在前面。比如写成(22,17,6,7)这种。
3.不下降子序列:不下降的意思是上升或者相同。
例:将元素 17,19,22取出来构成一个新序列 (17,19,22),这个序列中的每个元素均大于或等于前一个元素,22大于19,19大于17,因此,我们称这个序列为不下降子序列。再如将元素6,7,10,12,13取出来构成一个新序列(6,7,10,12,13),此序列符合不下降子序列的定义,因此它也是一个不下降子序列
4.最长不下降子序列: 子序列有很多,求出最长不下降子序列的意思是要求出一个子序列,它是不下降的,并且它在所有不下降的子序列中元素最多,这个最长不下降子序列可能有多个。
例:将元素6,7,10,12,13取出来构成一个新序列(6,7,10,12,13),此时它就是一个最长不下降子序列,长度为5。虽然(10,12,13)、(17,19,22)、(2,13)、(5,13)等等都是不下降子序列,但是它们的长度都不是最长的,因此不能称为最长不下降子序列。
二、解题方法
可以利用动态规划进行解题。在利用动态规划进行解题的时候,可以进一步划分为两种思路,分别是从前往后推理和从后往前推理。这两种思路都能够求出最长不下降子序列。
1.从前往后推理:依序求出以原序列中各元素分别为子序列结尾情况下能得出的最长不下降子序列
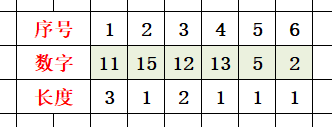
例子:以序列 (11,15,12,13,5,2)为例,通过从前往后推理求出最长不下降子序列的长度
以1号元素为子序列的结尾:此时最长不下降子序列长度为1,因为只有1号元素本身(11)
以2号元素为子序列的结尾:此时最长不下降子序列长度为2,此时包含1号元素和2号元素(11,15)
以3号元素为子序列的结尾:此时最长不下降子序列长度为2,此时包含1号元素和3号元素(11,12)
以4号元素为子序列的结尾:此时最长不下降子序列长度为3,此时包含1、3、4号元素(11,12,13)
以5号元素为子序列的结尾:此时最长不下降子序列长度为1,此时包含5号元素本身(5)
以6号元素为子序列的结尾:此时最长不下降子序列长度为1,此时包含6号元素本身(2)
如下图所示:
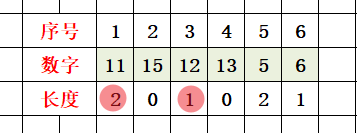
2.从后往前推理:依序求出以原序列中各元素分别为子序列起点情况下能得出的最长不下降子序列
以6号元素为子序列的起点:此时最长不下降子序列长度为1,因为只有6号元素本身(2)
以5号元素为子序列的起点:因为以5为起点,后面没有大于等于它的数字,此时最长不下降子序列长度为1,因为只有5号元素本身(5)
以4号元素为子序列的起点:因为以13为起点,后面没有大于等于它的数字,此时最长不下降子序列长度为1,因为只有4号元素本身(13)
以3号元素为子序列的起点:此时最长不下降子序列长度为2,此时包含3、4号元素(12,13)
以2号元素为子序列的起点:此时最长不下降子序列长度为1,后面没有大于等于它的数字,此时最长不下降子序列长度为1,因为只有2号元素本身(15)
以1号元素为子序列的起点:此时最长不下降子序列长度为3,此时包含1、3、4号元素(11,12,13)
3.总结:不管是从前往后推理,还是从后往前推理,都能够求出最长不下降的子序列的长度,其实动态规划就是一个填表的过程,上一个阶段的结果作为求下一个阶段求解的依据。针对这道题目,当我们求出以每个元素为起点或者终点的最长不下降子序列的长度之后,我们还需要找出整个长度行中的最大值,才能找到整个序列的最长不下降子序列长度。
三、代码解题
利用动态规划进行解题,需要找出3个必备条件。
- 确定状态
- 确定边界
- 确定状态转移方程
A.代码1(从前往后推理)
数据结构:
int f[1005]; f[i] 代表以第i号元素为终点最长不下降子序列的长度(确定状态)
int mx = -1; mx用来存放最终最长不下降子序列的长度大小
int data[1005]; data数组用来存放序列数字
输入序列数据和确定边界:
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
f[i]=1; //确定边界
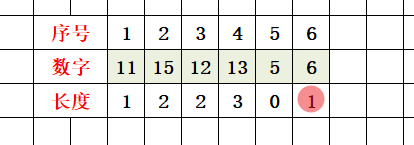
}其中 ,f[i]数组中的每个元素都需要初始化为1(确定边界),并不是只有f[1]需要初始化为1,其它元素都需要。为什么呢?假设我们只初始化f[1]=1,其它元素不初始化为1,以序列 (11,15,12,13,5,6)为例:
通过观察发现,本来在6号元素位置的长度f[6]应该为2,但是因为没有对f[i]每个元素初始化为1,使得f[6]=1,与我们的期望不符合
核心代码(状态转移方程):
for(int i=2;i<=n;i++)
{
for(int j=i-1;j>=1;j--)
{
if(a[i]>=a[j])
f[i]=max(f[i],f[j]+1);
}
}找出f[i[中的最大值,求出最长不下降子序列的长度
for(int i=1;i<=n;i++)
{
mx=max(mx,f[i]);
}完整代码
#include
#include
using namespace std;
int n;
int a[1001];
int f[1001];
int mx = -1;
int main() {
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
f[i]=1;
}
for(int i=2;i<=n;i++)
{
for(int j=i-1;j>=1;j--)
{
if(a[i]>=a[j])
f[i]=max(f[i],f[j]+1);
}
}
for(int i=1;i<=n;i++)
{
mx=max(mx,f[i]);
}
printf("%d",mx);
return 0;
}
B.代码2(从后往前推理)
数据结构:
int f[1005]; f[i] 代表以第i号元素为起点最长不下降子序列的长度(确定状态)
int mx = -1; mx用来存放最终最长不下降子序列的长度大小
int data[1005]; data数组用来存放序列数字
输入序列数据和确定边界:
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
f[i]=1; //确定边界
}其中 ,f[i]数组中的每个元素都需要初始化为1(确定边界),并不是只有f[n]需要初始化为1,其它元素都需要。为什么呢?假设我们只初始化f[n]=1,其它元素不初始化为1,以序列 (11,15,12,13,5,6)为例:
通过观察发现,本来在3号元素位置的长度f[3]应该为2,在1号元素位置的长度f[1]应该为3,但是因为没有对f[i]每个元素初始化为1,使得f[3]=1,f[1]=2,与我们的期望不符合
核心代码(状态转移方程):
for(int i=n-1;i>=1;i--)
{
for(int j=i+1;j<=n;j++)
{
if(a[i]<=a[j])
{
f[i]=max(f[i],f[j]+1);
}
}
}找出f[i[中的最大值,求出最长不下降子序列的长度
for(int i=1;i<=n;i++)
{
mx=max(mx,f[i]);
}完整代码
#include
#include
using namespace std;
int n;
int a[1001];
int f[1001]; //以第i项为起点的最长不下降子序列的长度
int mx = -1;
int main() {
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
f[i]=1;
}
for(int i=n-1;i>=1;i--)
{
for(int j=i+1;j<=n;j++)
{
if(a[i]<=a[j])
{
f[i]=max(f[i],f[j]+1);
}
}
}
for(int i=1;i<=n;i++)
{
mx=max(mx,f[i]);
}
printf("%d",mx);
return 0;
}
四、在线oj测试
写好代码之后,如何验证你写的是否正确呢?可以登录这个OJ,来测试代码的正确性
http://ybt.ssoier.cn:8088/problem_show.php?pid=1281
需要注意的是,该题求的是最长上升子序列,和最长不下降子序列还是有区别的需要稍微修改一下核心代码,上升子序列要求子序列中的元素不可以相同,而最长不下降子序列中的元素可以相同
可以做如下修改:
//从前往后退
for(int i=2;i<=n;i++)
{
for(int j=i-1;j>=1;j--)
{
if(a[i]>a[j])
f[i]=max(f[i],f[j]+1);
}
}
//从后往前推
for(int i=n-1;i>=1;i--)
{
for(int j=i+1;j<=n;j++)
{
if(a[i]五、提高拓展
以上只是求出的最长不下降子序列的长度,并没有输出最长不下降子序列中的各个元素,可以花点时间去思考一下怎么才能输出最长不下降子序列中的各个元素?。今天的题解就到这里啦 !如果有任何问题欢迎添加博主微信:Q1313135互相讨论学习。我们下期再见~~~