Polygon zkEVM中的Merkle tree

1. 引言

前序博客有：

• Merkle tree及其在区块链等领域的应用

以https://github.com/0xPolygonHermez/pil-stark为例，Polygon zkEVM中实现了2种Merkle tree（二者均采用Poseidon 哈希函数）：

• 1）基于Goldilocks域的Merkle tree：
  • 1.1）其Poseidon hash实现借鉴了https://github.com/filecoin-project/neptune（Poseidon hashing over BLS12-381）中的优化策略。
• 2）基于BN128域的Merkle tree：
  • 2.1）其Poseidon hash采用circomlibjs中的poseidon实现。

	if (starkStruct.verificationHashType == "GL") {
		// 借鉴了https://github.com/filecoin-project/neptune 中的优化策略
        const poseidon = await buildPoseidonGL();
        MH = await buildMerklehashGL();
        transcript = new Transcript(poseidon);
    } else if (starkStruct.verificationHashType == "BN128") {
        const poseidonBN128 = await buildPoseidonBN128();
        MH = await buildMerklehashBN128();
        transcript = new TranscriptBN128(poseidonBN128);
    } else {
        throw new Error("Invalid Hash Type: "+ starkStruct.verificationHashType);
    }

Polygon zkEVM中包含的Merkle tree主要有：【详细可看Polygon zkEVM公式梳理】

• tree1：对应PIL中各commit多项式扩域evaluation值。
• tree2：对应PIL中各plookup约束扩域evaluation值。
• tree3：对应PIL中各plookup/permutation/connection约束Z多项式扩域evaluation值。
• tree4：对应PIL中标记为Q的多项式（如中间多项式约束表达（Goldilocks基域）和合并的polIdentities约束约束表达（Goldilocks extension 3 域））扩域evaluation值——ctx.q_2ns。
• constTree：对应PIL中各constant多项式扩域evaluation值。
• FRI证明中，starkStruct.steps.length数量个Merkle tree：tree[si]

FRI 折叠Merkle化证明配置信息starkStruct为：

{
	"nBits": 10, //待证明FRI多项式的degree为2^nBits
	"nBitsExt": 11,
	"nQueries": 8,
	"verificationHashType": "GL",
	"steps": [
		{"nBits": 11}, //第一个step的nBits值必须等于上面的nBitsExt
		{"nBits": 7},
		{"nBits": 3}
	]
}

FRI 折叠Merkle化证明核心代码为：

	async prove(transcript, pol, queryPol) {
        const self = this;
        const proof = [];
        const F = this.F;

        let polBits = log2(pol.length);
        assert(1<<polBits == pol.length, "Invalid poluynomial size");    // Check the input polynomial is a power of 2
        assert(polBits == this.inNBits, "Invalid polynomial size");

        let shiftInv = F.shiftInv;
        let shift = F.shift;
        let tree = [];

        for (let si = 0; si<this.steps.length; si++) proof[si] = {};
        for (let si = 0; si<this.steps.length; si++) {
            const reductionBits = polBits - this.steps[si].nBits;

            const pol2N = 1 << (polBits - reductionBits);
            const nX = pol.length / pol2N;

            const pol2_e = new Array(pol2N);

            let special_x = transcript.getField();

            let sinv = shiftInv;
            const wi = F.inv(F.w[polBits]);
            for (let g = 0; g<pol.length/nX; g++) {
                if (si==0) {
                    pol2_e[g] = pol[g];
                } else {
                    const ppar = new Array(nX);
                    for (let i=0; i<nX; i++) {
                        ppar[i] = pol[(i*pol2N)+g];
                    }
                    const ppar_c = F.ifft(ppar);
                    const zyd_e = evalPol(F, ppar_c, F.mul(sinv, special_x));
                    polMulAxi(F, ppar_c, F.one, sinv);    // Multiplies coefs by 1, shiftInv, shiftInv^2, shiftInv^3, ......        

                    pol2_e[g] = evalPol(F, ppar_c, special_x);
                    assert(F.eq(zyd_e, pol2_e[g]));
                    sinv = F.mul(sinv, wi);
                }
            }


            if (si < this.steps.length-1) {
                const nGroups = 1<< this.steps[si+1].nBits;

                let groupSize = (1 << this.steps[si].nBits) / nGroups;


                const pol2_etb = getTransposedBuffer(pol2_e, this.steps[si+1].nBits);

                tree[si] = await this.MH.merkelize(pol2_etb, 3* groupSize, nGroups);

                proof[si+1].root= this.MH.root(tree[si]);
                transcript.put(this.MH.root(tree[si]));
            } else {
                for (let i=0; i<pol2_e.length; i++) {
                    transcript.put(pol2_e[i]);
                }
            }

            pol = pol2_e;
            polBits = polBits-reductionBits;

            for (let j=0; j<reductionBits; j++) {
                shiftInv = F.mul(shiftInv, shiftInv);
                shift = F.mul(shift, shift);
            }
        }
       	// ...........
    }

参考V神博客 STARKs, Part 3: Into the Weeds：

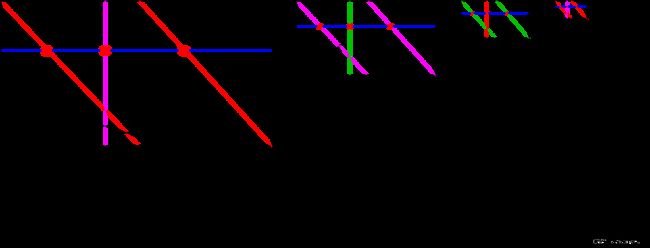
pol为待证明FRI多项式$\text{pol}(X)$的点值表示：【其中引入$g$实现Coset-FRI。】
$\{(g{w}_e^0,\text{pol}(g{w}_e^0)),(g{w}_e^1,\text{pol}(g{w}_e^1)),(g{w}_e^2,\text{pol}(g{w}_e^2)),\cdots (g{w}_e^{2^{\text{nBitsExt}}-1},\text{pol}(g{w}_e^{2^{\text{nBitsExt}}-1}))\}$
待证明FRI多项式$\text{pol}(X)$的degree为$N=2^{\text{nBits}}$，$X$取自于由$w=g{w}_e$生成元派生的域，其中$w_e^{2^{\text{nBitsExt}}}=1$。

【以上代码中const wi = F.inv(F.w[polBits]);中wi满足${\text{wi}}^{2^{\text{steps[i-1].nBits}}}=1$】

• 在Step0：有$\text{reductionBits\_0=nBitsExt-steps[0].nBits}=0，{\text{nX}}_0=2^{\text{reductionBits\_0}}=1，{\text{pol2N}}_0=2^{\text{nBitsExt - reductionBits\_0}}=2^{\text{steps[0].nBits}}$，构建的多项式：
  • ${\text{pol2\_e}}_0(X_0)=\text{pol}(X)=\text{pol}(X,X^{{\text{nX}}_0})=\text{pol}(X,X)$，
  • ${\text{pol2\_e}}_0(X_0)$的degree为$N_0=2^{(\text{steps[0].nBits}-1)}$，
  • $X_0$取自于由$w_0=(g{w}_e{)}^{{\text{nX}}_0}=(g{w}_e)=(g\cdot \text{wi\_0})$ 生成元派生的域，其中$w_e^{2^{\text{nBitsExt}}}=1，{\text{wi\_0}}^{2^{\text{steps[i-1].nBits}}}={\text{wi\_0}}^{2^{\text{nBitsExt}}}=1$。
• 在Step1：有$\text{reductionBits\_1=steps[0].nBits-steps[1].nBits}，{\text{nX}}_1=2^{\text{reductionBits\_1}}，{\text{pol2N}}_1=2^{\text{steps[0].nBits - reductionBits\_1}}=2^{\text{steps[1].nBits}}$，构建的多项式${\text{pol2\_e}}_1(X_1)$为${\text{pol2\_e}}_0(X_0,X_0^{{\text{nX}}_1})$在$\text{special\_x\_1}$处的多项式，有：
  • ${\text{pol2\_e}}_1(X_1)={\text{pol2\_e}}_0(\text{special\_x\_1},X_0^{{\text{nX}}_1})$，
  • ${\text{pol2\_e}}_1(X_1)$的degree为$N_1=2^{(\text{steps[1].nBits}-1)}$，
  • $X_1$取自于由$w_1=w_0^{{\text{nX}}_1}=(g{w}_e{)}^{{\text{nX}}_0\cdot {\text{nX}}_1}=(g{w}_e{)}^{2^{\text{reductionBits\_0}+\text{reductionBits\_1}}}=(g^{2^{\text{reductionBits\_0}+\text{reductionBits\_1}}}\cdot \text{wi\_1})$生成元派生的域，其中$w_e^{2^{\text{nBitsExt}}}=1，{\text{wi\_1}}^{2^{\text{steps[i-1].nBits}}}={\text{wi\_1}}^{2^{\text{steps[0].nBits}}}=1$。
• 在Stepi：有$\text{reductionBits\_i=steps[i-1].nBits-steps[i].nBits}，{\text{nX}}_i=2^{\text{reductionBits\_i}}，{\text{pol2N}}_i=2^{\text{steps[i-1].nBits - reductionBits\_i}}=2^{\text{steps[i].nBits}}$，构建的多项式${\text{pol2\_e}}_i(X_i)$为${\text{pol2\_e}}_{i-1}(X_{i-1},X^{{\text{nX}}_i})$在$\text{special\_x\_i}$处的多项式，有：
  • ${\text{pol2\_e}}_i(X_i)={\text{pol2\_e}}_{i-1}(\text{special\_x\_i},X^{{\text{nX}}_i})$，
  • ${\text{pol2\_e}}_i(X_i)$的degree为$N_i=2^{(\text{steps[i].nBits}-1)}$，
  • $X_i$取自于由$w_i=w_{i-1}^{{\text{nX}}_i}=(g{w}_e{)}^{{\text{nX}}_0\cdot {\text{nX}}_1\cdots \cdot {\text{nX}}_i}=(g{w}_e{)}^{2^{{\sum }_{j=0}^i\text{reductionBits\_j}}}=(g^{2^{{\sum }_{j=0}^i\text{reductionBits\_j}}}\cdot \text{wi\_i})$生成元派生的域，其中$w_e^{2^{\text{nBitsExt}}}=1，{\text{wi\_i}}^{2^{\text{steps[i-1].nBits}}}=1$。

2. Polygon zkEVM中基于Goldilocks域的Merkle tree

2.1 基于Goldilocks域的Poseidon hash实现

前序博客有：

• POSEIDON: A New Hash Function for Zero-Knowledge Proof Systems 学习笔记

基于Goldilocks域的Merkle tree，其Poseidon hash实现借鉴了https://github.com/filecoin-project/neptune（Poseidon hashing over BLS12-381）中的优化策略，其基于的是Goldilocks extension 3 field。
详细代码实现见pil-Stark项目中的poseidon.js。

2.2 基于Goldilocks域的LinearHash

pil-stark项目中的 linearhash.js中，LinearHash类中，主要实现了hash函数：【将输入vals铺平展开为flatVals：若展开后的flatVals长度小于等于4，则补零为长度为4的结果返回；否则，将flatVals补齐为最近的8的整数倍，以8个元素为一组inHash，递归调用poseidon，返回最后一次调用poseidon函数的结果。】

module.exports = class LinearHash {

    constructor(poseidon) {
        this.H = poseidon; //基于Goldilocks域的Poseidon hash
    }

    hash(vals) { //输入为vals数组，每个元素也可能是数组
        const flatVals = [];//将输入vals展开铺平存入flatVals中。
        for (let i=0; i<vals.length; i++) {
            if (Array.isArray(vals[i])) {
                for (let j=0; j<vals[i].length; j++) {
                    flatVals.push(vals[i][j]);
                }
            } else {
                flatVals.push(vals[i]);
            }
        }
        let st = [0n, 0n, 0n, 0n];
        //若flatVals长度小于4，则在其后补零到长度为4.
        if (flatVals.length <= 4) { 
            for (let i=0; i<flatVals.length;i++)  {
                st[i] = flatVals[i];
            }
            return st;
        }
        let inHash = [];
        for (let i=0; i<flatVals.length;i++) {
            inHash.push(flatVals[i]);
            //将铺平后的flatVals，每8个元素为一组inHash，递归调用poseidon函数
            if (inHash.length == 8) {
                st = this.H(inHash, st);//递归调用，st为输入和输入
                inHash.length = 0;
            }
        }
        //若铺平后的flatVals长度不是8的整数倍，则后续补零到为最近的8的整数倍。
        if (inHash.length>0) {
            while (inHash.length<8) inHash.push(0n);
            //对补零后的inHash块，递归调用poseidon
            st = this.H(inHash, st);
        }
        //返回最后一次调用poseidon的结果
        return st;
    }
}

linearHash函数功能为：

• 1）将输入buffIn以width列，height行矩阵表示；（每列元素为Goldilocks基域元素）
• 2）若width列数小于等于4，则之间将以width列，height行矩阵表示的buffIn赋值给buffOut，返回buffOut。

  if (width <=4) {
      for (let i=0; i<heigth; i++) {
          for (let j=0; j<width; j++) {
              buffOut[i*4+j] = buffIn[width*i + j];
          }
      }
      return buffOut;
  }
  

• 3）接下来为width列数大于4的情况：
  调用buildWasm，会实现wasm代码，公开基于Goldilocks域的add/mul/square/poseidon/multiLinearHash/merkelizeLevel函数。
  调用glwasm.multiLinearHash(pIn, width, heigth, pOut);，其中pIn以矩阵表示，具有width列，height行。（每列元素为Goldilocks基域元素）。multiLinearHash是指将每8个元素为一组调用poseidon函数进行运算。pOut的大小为：height*4。【为所有的叶子节点】
  将返回的pOut（res）值更新到tree.nodes中：

  for (let i=0; i<res.length; i++) { //设置所有叶子节点
  	tree.nodes.set(res[i], i*nPerThreadF*4);
  }
  

• 4）构建叶子节点之上的中间节点：

  	let pIn = 0;
      let n64 = height*4;
      let nextN64 = (Math.floor((n64-1)/8)+1)*4;
      let pOut = pIn + nextN64*2*8;
      while (n64>4) {
          // FIll with zeros if n nodes in the leve is not even
          await _merkelizeLevel(tree.nodes, pIn, nextN64/4, pOut);
  
          n64 = nextN64;
          nextN64 = (Math.floor((n64-1)/8)+1)*4;
          pIn = pOut;
          pOut = pIn + nextN64*2*8;
      }
  

2.3 基于Goldilocks域的Merkle tree

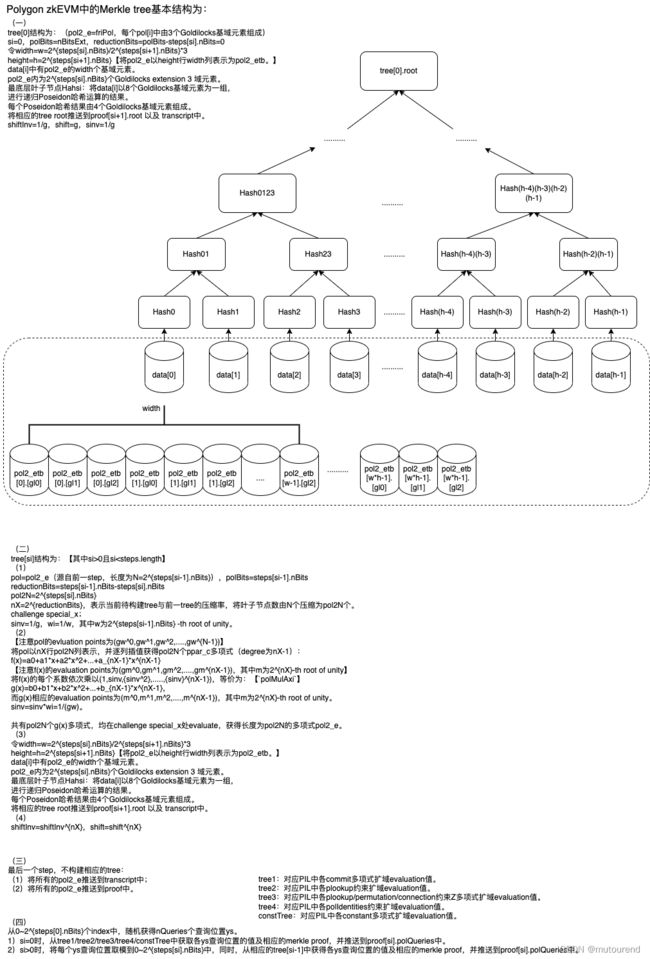
基于Goldilocks域的Merkle tree的基本结构为：

		const tree = {
			//为待Merkle化的所有元素，以矩阵表示，具有w列h行。
			//buff每个元素基于Goldilocks extension 3 域，
			//所以，buff每个元素由3个Goldilocks基域元素组成。
            elements: buff, 
             //若h=2^n，则nodes总数为: (2^{n+1}-1)*4，即每个节点可存放4个Goldilocks基域元素。
            nodes: new BigUint64Array(this._getNNodes(height*4)),
            width: width, //为待Merkle化元素矩阵表示的列数w * 3（因基于Goldilocks extension 3 域）。
            height: height //为待Merkle化元素矩阵表示的行数h，假设h=2^n
        };

tree[si] = await this.MH.merkelize(pol2_etb, 3* groupSize, nGroups);，其中：

• groupSize为$2^{\text{steps[si].nBits}}/2^{\text{steps[si+1].nBits}}$（$\text{groupSize}\ast 3$为width，因基于的是Goldilocks extension 3 域）
• nGroups为$2^{\text{steps[si+1].nBits}}$（nGroups即为height）
• pol2_eth的长度为$\text{nGroups*groupSize}$，总的Goldilocks基域元素数为$\text{width * height}$。

在将某输入Merkle化（merkelize）的过程中：

• 1）分组从待Merkle化buff取输入bb（以矩阵表示，width列和curN行个元素（每3个列元素组成一个val）），调用linearHash函数：

  	for (let i=0; i< height; i+=nPerThreadF) {
          const curN = Math.min(nPerThreadF, height-i);
          console.log("slicing buff "+i);
          const bb = tree.elements.slice(i*width, (i+curN)*width);
  	    // const bb = new BigUint64Array(tree.elements.buffer, tree.elements.byteOffset + i*width*8, curN*width);
          if (self.useThreads) {
              console.log("creating thread "+i);
              promisesLH.push(pool.exec("linearHash", [bb, width, i, height]));
          } else { //详细的linearHash实现见上一节分析。
              res.push(await linearHash(bb, width, i, curN));
          }
      }
  

• 2）更新tree.nodes的所有叶子节点：

  	for (let i=0; i<res.length; i++) {
          tree.nodes.set(res[i], i*nPerThreadF*4);
      }
  

• 3）构建叶子节点之上的中间节点（包括root节点）：

  	let pIn = 0;
      let n64 = height*4;
      let nextN64 = (Math.floor((n64-1)/8)+1)*4;
      let pOut = pIn + nextN64*2*8;
      while (n64>4) {
          // FIll with zeros if n nodes in the leve is not even
          await _merkelizeLevel(tree.nodes, pIn, nextN64/4, pOut);
  
          n64 = nextN64;
          nextN64 = (Math.floor((n64-1)/8)+1)*4;
          pIn = pOut;
          pOut = pIn + nextN64*2*8;
      }
  

3. Polygon zkEVM中基于BN128域的Merkle tree

附录：Polygon Hermez 2.0 zkEVM系列博客

• ZK-Rollups工作原理
• Polygon zkEVM——Hermez 2.0简介
• Polygon zkEVM网络节点
• Polygon zkEVM 基本概念
• Polygon zkEVM Prover
• Polygon zkEVM工具——PIL和CIRCOM
• Polygon zkEVM节点代码解析
• Polygon zkEVM的pil-stark Fibonacci状态机初体验
• Polygon zkEVM的pil-stark Fibonacci状态机代码解析
• Polygon zkEVM PIL编译器——pilcom 代码解析
• Polygon zkEVM Arithmetic状态机
• Polygon zkEVM中的常量多项式
• Polygon zkEVM Binary状态机
• Polygon zkEVM Memory状态机
• Polygon zkEVM Memory Align状态机
• Polygon zkEVM zkASM编译器——zkasmcom
• Polygon zkEVM哈希状态机——Keccak-256和Poseidon
• Polygon zkEVM zkASM语法
• Polygon zkEVM可验证计算简单状态机示例
• Polygon zkEVM zkASM 与 以太坊虚拟机opcode 对应集合
• Polygon zkEVM zkROM代码解析（1）
• Polygon zkEVM zkASM中的函数集合
• Polygon zkEVM zkROM代码解析（2）
• Polygon zkEVM zkROM代码解析（3）
• Polygon zkEVM公式梳理

附录A：wasmbuilder

https://github.com/iden3/wasmbuilder——wasmbuilder：为手写构造wasm代码的Javascript库。