LeetCode53. 最大子数组和

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/maximum-subarray
链接：https://leetcode-cn.com/problems/maximum-subarray/solution/dong-tai-gui-hua-fen-zhi-fa-python-dai-ma-java-dai/

给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。
子数组 是数组中的一个连续部分。

示例 1：

输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
输出：6
解释：连续子数组 [4,-1,2,1] 的和最大，为 6 。
示例 2：

输入：nums = [1]
输出：1
示例 3：

输入：nums = [5,4,-1,7,8]
输出：23

（1）
动态规划问题

李煜东著《算法竞赛进阶指南》，摘录如下：：

为了保证计算子问题能够按照顺序、不重复地进行，
动态规划要求已经求解的子问题不受后续阶段的影响。这个条件也被叫做「无后效性」。
换言之，动态规划对状态空间的遍历构成一张有向无环图，遍历就是该有向无环图的一个拓扑序。有向无环图中的节点对应问题中的「状态」，图中的边则对应状态之间的「转移」，转移的选取就是动态规划中的「决策」。

不空间优化的代码

class Solution:
    def maxSubArray(self, nums: List[int]) -> int:
        size = len(nums)
        if size == 0:  # 空列表，返回最大和0
            return 0
        dp = [0 for _ in range(size)]
        print(dp)  # dp是和nums长度相等的列表，值均为0

        dp[0] = nums[0]
        for i in range(1, size):  # 从第二个遍历到最后
            if dp[i - 1] >= 0:  # 如果第i-1个数大于等于0，则这个数可以被加到列表
                dp[i] = dp[i - 1] + nums[i]
            else:
                dp[i] = nums[i]  # 第i个数必选的
        return max(dp)

空间优化的代码

from typing import List
#这个List类在typing类中

class Solution:
    def maxSubArray(self, nums: List[int]) -> int:
        size = len(nums)
        pre = 0
        res = nums[0]
        for i in range(size):
            pre = max(nums[i], pre + nums[i])
            res = max(res, pre)
        return res

（2）分治法
分治法的思路是这样的，其实也是分类讨论。

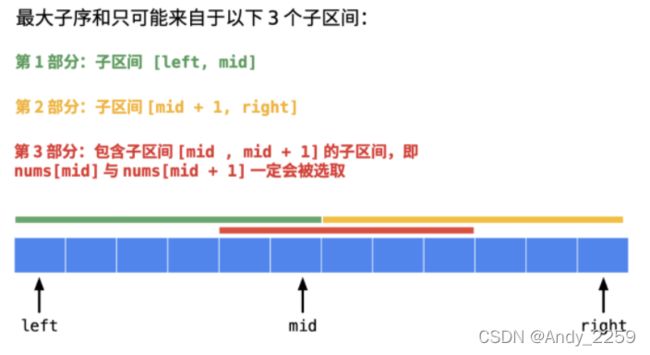
连续子序列的最大和主要由这三部分子区间里元素的最大和得到：

第 1 部分：子区间 [left, mid]；
第 2 部分：子区间 [mid + 1, right]；
第 3 部分：包含子区间 [mid , mid + 1] 的子区间，即 nums[mid] 与 nums[mid + 1] 一定会被选取。
对这三个部分求最大值即可。
说明：考虑第 3 部分跨越两个区间的连续子数组的时候，由于 nums[mid] 与 nums[mid + 1] 一定会被选取，可以从中间向两边扩散，扩散到底 选出最大值，

这个有点没整明白

from typing import List


class Solution:
    def maxSubArray(self, nums: List[int]) -> int:
        size = len(nums)
        if size == 0:
            return 0
        return self.__max_sub_array(nums, 0, size - 1)

    def __max_sub_array(self, nums, left, right):
        if left == right:
            return nums[left]
        mid = (left + right) >> 1
        return max(self.__max_sub_array(nums, left, mid),
                   self.__max_sub_array(nums, mid + 1, right),
                   self.__max_cross_array(nums, left, mid, right))

    def __max_cross_array(self, nums, left, mid, right):
        # 一定包含 nums[mid] 元素的最大连续子数组的和，
        # 思路是看看左边"扩散到底"，得到一个最大数，右边"扩散到底"得到一个最大数
        # 然后再加上中间数
        left_sum_max = 0
        start_left = mid - 1
        s1 = 0
        while start_left >= left:
            s1 += nums[start_left]
            left_sum_max = max(left_sum_max, s1)
            start_left -= 1

        right_sum_max = 0
        start_right = mid + 1
        s2 = 0
        while start_right <= right:
            s2 += nums[start_right]
            right_sum_max = max(right_sum_max, s2)
            start_right += 1
        return left_sum_max + nums[mid] + right_sum_max