LeetCode207.课程表
看完题我就想,这不就是进程里面的死锁问题嘛,进程1等进程2释放锁,进程2等进程3释放锁,进程3等进程1释放锁,这就造成了死锁。或者是spring中的循环依赖问题,BeanA的初始化需要初始化一个BeanB,BeanB的初始化需要初始化BeanA就出现了循环依赖。
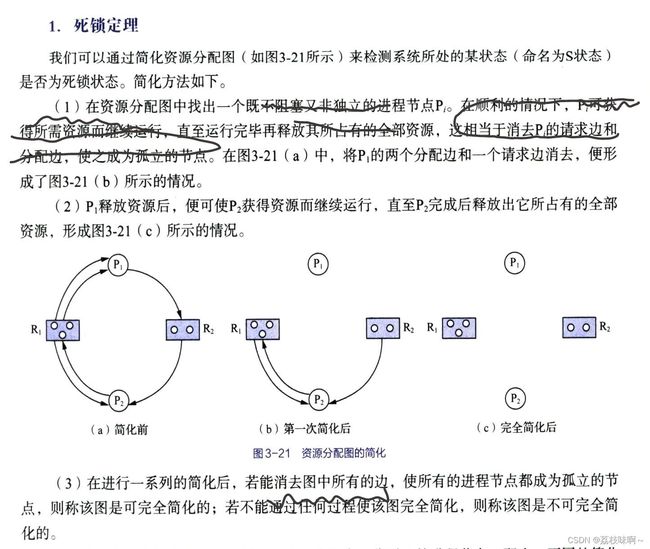
我记得的死锁的判断是用简化图的方式,先找出能最先完成的进程,然后把这个点消掉,再找在等待这个进程的进程里面最容易完成看看能不能消掉,消到最后不能消,如果有环就会死锁
而spring中解决循环依赖问题用的是三级缓存就与这道题无关了
如果用简化图就太麻烦了,我就想用hashmap,我把prerequisites数组里的数据以k-v的形式存在HashMap里面,然后用get方法去拿到请求链中的节点放到一个set里面,如果这个节点早就在set中那么就出现了循环,于是几分钟就写出了下面的代码:
class Solution {
public boolean canFinish(int numCourses, int[][] prerequisites) {
int n = prerequisites.length;
Map map = new HashMap<>();
for(int i=0;i set = new HashSet<>();
set.add(key);
while(map.containsKey(key)){
if(set.contains(map.get(key))){
return false;
}else{
key = map.get(key);
set.add(key);
}
}
}
return true;
}
} 然后出错了,
因为我忽略了一门课的选修课有多门,hashmap如果key相同后面的value会覆盖前面的value。然后自己想了很久写没想出来然后就看题解了。
class Solution {
List> edges;
int visit[];
boolean valid = true;
public boolean canFinish(int numCourses, int[][] prerequisites) {
edges = new ArrayList>();
for(int i=0;i());
}
visit = new int[numCourses];
for(int[] info : prerequisites){
edges.get(info[0]).add(info[1]);
}
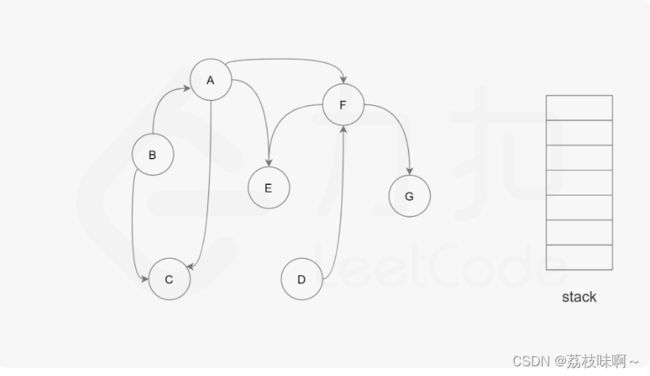
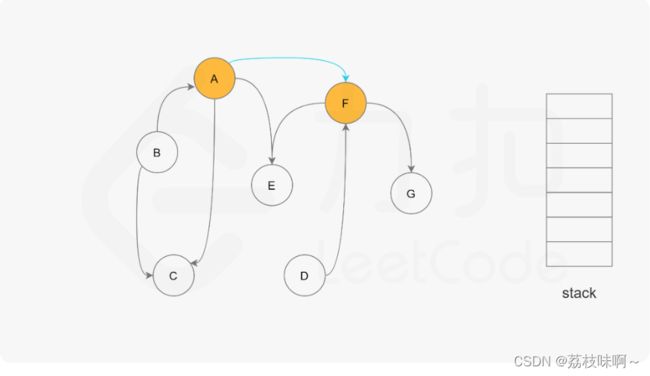
for(int i=0;i 题解用的是深度优先搜索。如果我们把课程作为他的先修课的先行节点,我们可以得到一个图
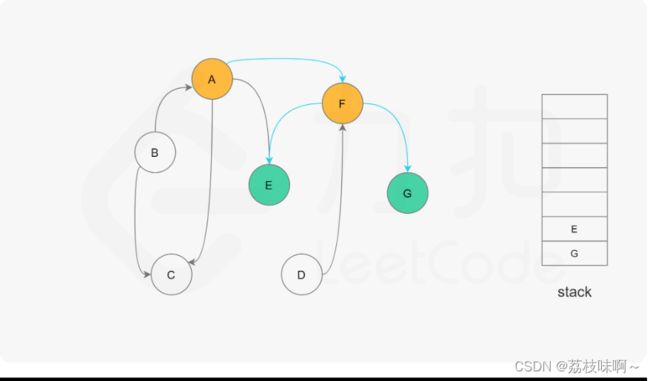
比如这个图就是要学A就必须先学F,E,C,要学F必须先学E,G,而E和G不需要先学其他课程,所以可以先把E和G学了然后F也可以学了....
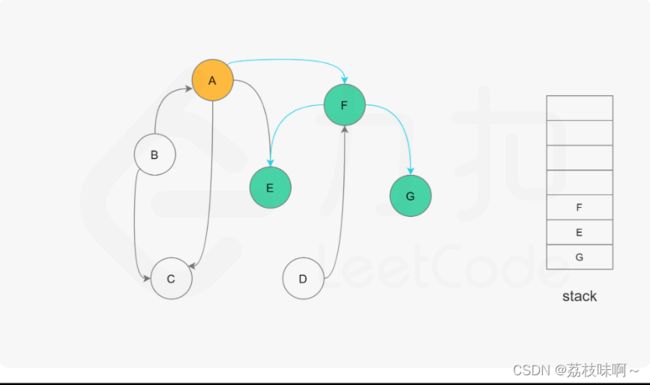
题解用的是深度优先遍历可以结合下面的图更方便理解
它用List
然后先看dfs()方法:
public void dfs(int u){
visit[u] = 1;
for(int v : edges.get(u)){
if(visit[v] == 0){
dfs(v);
if(valid == false){
return;
}
}else if(visit[v] == 1){
valid = false;
return;
}
}
visit[u] = 2;
}课程u进入dfs后先把visit[u]从0改成1,表示正在访问u节点,然后通过edges.get(u),拿到u课程的所有先修课程vv,然后对这些先修课程v进行判断,
如果先修课程v的visit[v]=0,表示还没有搜索这个课程,递归调用dfs对它进行搜索;
如果visit[v]=1说明这个课程节点在之前已经开始搜索了但是还没有完成搜索,而又重新回到了这个节点,说明出现了环,那么就把valid改成false直接返回;
所以在前面visit[v]=0的情况下,dfs完了,如果valid变成了false就可以直接返回。
所以当visit[v]=2的时候,表示可以搜索到,不用做任何操作,直接进入判断下一个先行课;
当u的所有先修课程都判断完了并且没有出现valid改成fasle返回的情况,那么表明u的所有先修课都可以搜索到,那么u也可以搜索到了,把visit[u]改成2。
然后再看主方法:
public boolean canFinish(int numCourses, int[][] prerequisites) {
edges = new ArrayList>();
for(int i=0;i());
}
visit = new int[numCourses];
for(int[] info : prerequisites){
edges.get(info[0]).add(info[1]);
}
for(int i=0;i 先对edges创建一个外层的List,然后再用for循环在这个外层List的每个节点上创建一个Lsit,创建一个visit数组,这都是初始化操作。然后再看下面这个for,他是edges.get(info[0])拿到了外层节点,然后再add(info[1])把先修课挂在了这个节点上,
题解用的是edges.get(info[1]).add(info[0]),我改成了edges.get(info[0]).add(info[1]),因为我觉得这样更好理解,两种都可以跑通。题解是按照上面的图来的,以课程作为他的先修课的先行节点,题解它其实是一个反向图,我们的目的是要判断有没有循环依赖,也就是有没有环,而有没有环与方向的正反无关。
然后只要把所有课程都dfs一遍就可以,for循环里面可以加上&&valid条件,这样一旦fasle后面就不用判断了,效率可以提高一点。