混沌系统在图像加密中的应用（荷控忆阻器的混沌电路）

前言

忆阻混沌电路是一种基于忆阻器的电路，可以产生复杂的非线性动力学行为，即混沌行为。它是通过将忆阻器与其他电子元件组合在一起，形成一个反馈环路来实现的。忆阻混沌电路具有以下主要组成部分：

（1）忆阻器：忆阻器是电路中的核心元件，其电阻值随时间和输入电流的变化而变化。它能够保持电荷或电流的历史状态，并且可以通过施加电压或电流来改变其电阻值。忆阻器通过在其电路中引入非线性特性，为电路引入了记忆性和非线性响应，从而产生了混沌行为。
（2）电容器：电容器用于存储电荷并产生电场。在忆阻混沌电路中，电容器可以与忆阻器一起构成一个RC环路，从而产生反馈。
（3）电感器（可选）：电感器用于存储磁能，并产生磁场。在一些忆阻混沌电路中，电感器可以与其他元件一起组成RLC环路，增强电路的非线性和混沌特性。
（4）运算放大器：运算放大器用于将电路的输出信号放大，并将其反馈回输入端。它对忆阻混沌电路中的信号放大和反馈起着重要作用。

忆阻器(Memristor)是 Chua从理论上预测的电路的第四个基本元件，其电阻的非线性特征是由电荷 q 和磁通 φ 定义的，这个电路变量是其他三个基本元件无法替代的，磁通量φ按电荷q 的改变率称之为“忆阻值”：

根据法拉第电磁感应定律和求导法则，流经忆阻器的电压和电流具有如下关系式

一、什么是电荷控制型忆阻器

电荷控制型忆阻器（Charge-Controlled Memristor）是一种特殊类型的忆阻器，其电阻值（阻抗）取决于通过它的电荷量。

电荷控制型忆阻器的工作机制与电荷在忆阻器中的积累和释放有关。在一个电荷控制型忆阻器中，当通过它的电流或电荷超过一个阈值时，忆阻器的电阻值将发生变化。进一步的电荷输入将导致电阻值继续增加，而电荷释放则将导致电阻值减小。

这种电荷控制机制可以实现类似生物突触的行为，其中突触的强度（权重）取决于之前突触上通过的电荷量。这种忆阻器的行为在神经网络和模拟突触器的研究中具有应用价值，可以用于构建具有类似人脑的计算模型。

二、双荷控忆阻器的混沌电路设计

本节内容选取了论文《含两个荷控忆阻器最简混沌电路的设计与研究》来进行研究。如图1所示含两个荷控忆阻器的混沌电路，除了两个忆阻器外只用了四个元件，两个电感，一个负电导和一个电容，电路巧妙采用了串并联形式。由于忆阻器是无源器件，为了使电路产生振荡，将一个负电导与其中一个忆阻器串联，另一个忆阻器与电感串联。在这个电路里两个忆阻器是完全相同的，其表达式用式(1)~(2)表示，其中式(2)是忆阻器内部状态控制表达式。


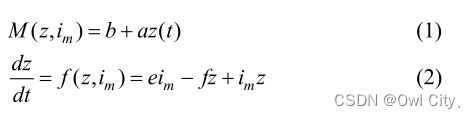
其中 ， a, b, e, f 为参数， z 为荷控忆阻器的内部状态变量。
电路中两个电感 L 是完全相同的。根据基尔霍夫电压和电流定律以及元件的伏安特性，图 1 所示的电路状态方程可以表示为

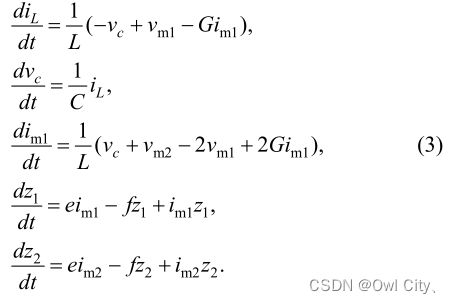
方程中所对应的的五个状态变量分别为(iL，vC，im1，z1，z2)，其中的 z1、z2 为两个忆阻器内部状态变量。

三、双荷控忆阻器的混沌电路特性分析

1.时序图和相图

选择参数 L=0.4 H，a=0.5，b=0.5，G=1.5 S，e=0.3，f=1.0，C=0.1 F，采用ODE45方法计算得到系统(3)的仿真结
果。

（1）以下是5个变量的波形图，说明随时间变化具有非周期性，处于混沌状态。

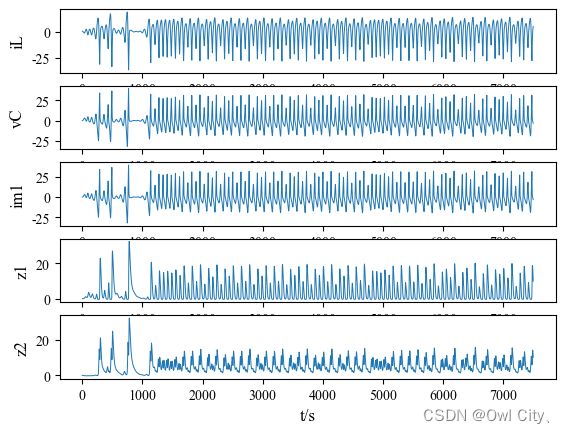
（2）下图仿真了忆阻器 z1 和 z2 的伏安特性曲线，发现这两个相同的忆阻器连接在不同支路中，各自的 vm和 im在不同范围内变化，伏安特性是不同的，但两个忆阻器电阻具有相似的非线性特点，具有忆阻器典型的斜体“8”字形紧磁滞回线特性，而且是每次的轨线不重复的混沌态。

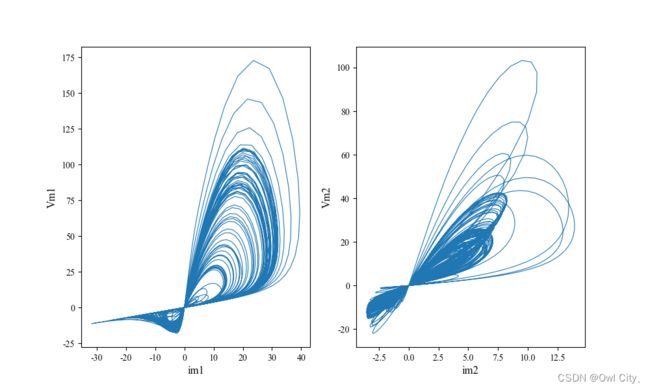
（3）根据忆阻器无源定理，荷控忆阻器的有源性或无源性可用 M(q) 来表征，即当 M(q)≥0 时表示忆阻器是无源的，否则表示忆阻器呈现为有源性。从下图 im–pm 关系图可以判断这两个忆阻器的即时功率恒为正值，表明都是无源的，而且忆阻器吸收功率随时间变化的，呈混沌态。

2.功率谱和庞加莱截面映射

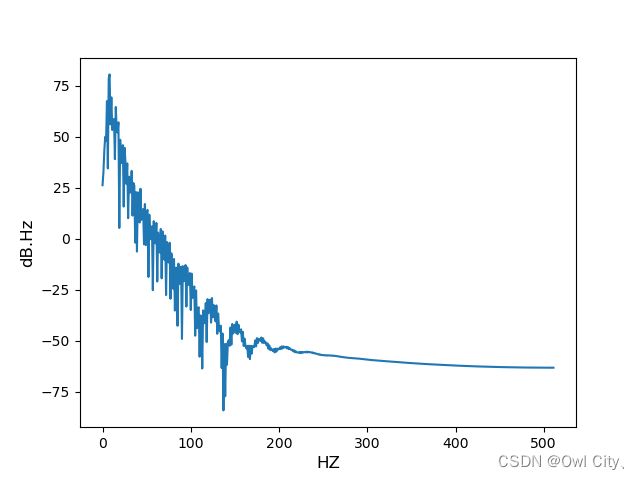
功率谱是一种用于研究信号频率特性的工具。混沌系统产生的信号通常具有非常复杂的频谱结构，功率谱可以帮助我们理解信号的频域分布情况。可以看出该系统的频谱分布较为广泛、连续的，则说明系统的运动是随机的。其中

横坐标：横坐标表示频率，以赫兹（Hz）或者角频率（rad/s）作为单位。频率表示信号中不同频率分量的存在。低频信号的频率较低，高频信号的频率较高。
纵坐标：纵坐标表示功率或能量。功率谱表示了信号在不同频率上的功率或能量分布。

庞加莱截面映射（Poincaré section mapping）是一种在动力系统中用于研究混沌行为的方法。它是根据亨利·庞加莱（Henri Poincaré）的工作而命名的，他在19世纪末首次使用这种映射来研究三体问题中的混沌现象。庞加莱截面映射基于以下观察：对于一个具有混沌行为的动力系统，使其在高维相空间中的轨迹变得难以理解和分析。然而，通过选择适当的平面（截面），我们可以将高维相空间的轨迹投影到较低维的平面上，从而更容易进行分析。

下图分别是系统在 y=0 和 z=10 两个截面上的庞加莱截面图。这两个图都是由具有一些线和一定形状的带状图案组成，说明系统的运动既具有确定性又具有随机性，是混沌系统。

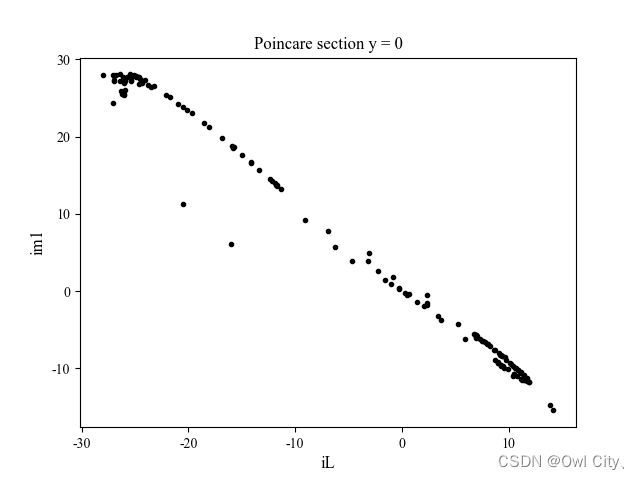
3.平衡点及其稳定性分析

4.分岔图L-Vc

混沌系统的分岔图（Bifurcation diagram）是一种用于可视化系统演化过程中的稳定性和周期性的工具。在混沌系统中，微小的参数变化可能会导致系统的行为发生显著变化，从而产生分岔现象。混沌系统的分岔图通常使用系统参数作为横坐标，而系统状态、稳定点或周期轨道的值作为纵坐标。通过系统参数的逐步改变，我们可以观察到纵坐标上的分岔现象。每一个参数值对应一个系统状态，而分岔图显示了这些状态的演化。

下图是 G=1.75 时，L 在[0.4,1.0]区间变化的分岔图，L 在[0.4,0.58]区间系统处于混沌状态，在 L>0.63 之后出现倒分岔现象.

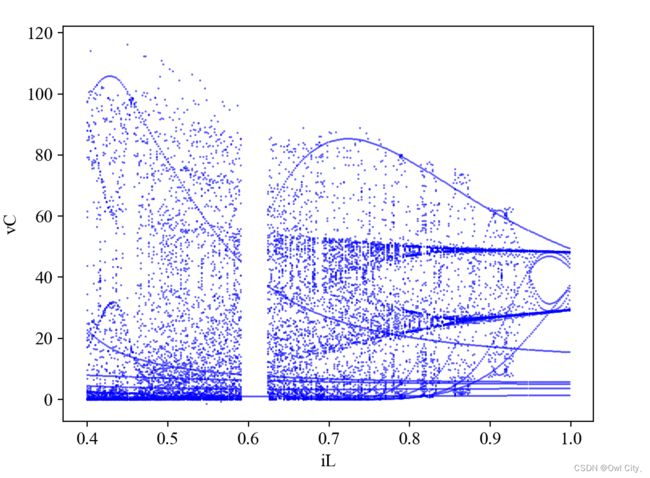
四、拓展

读者可以自行更改忆阻器的位置和数量并调整参数来创造不同的荷控忆阻器的混沌电路。也可以去对照原文改进，网址：
https://www.china-simulation.com/CN/1004-731X/home.shtml

五、python代码

这里我给出了相图、时序图代码，读者可自行加以完善和改进。

import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt

def dmove(Point, t, sets):
    a, b, C, e, f, G, L = sets
    iL, vC, im1, z1, z2 = Point
    im2 = -iL - im1
    vm1 = (b + a * z1) * im1
    vm2 = (b + a * z2) * im2
    return np.array([1/L * (-vC + vm1 - G * im1),
                     1/C * iL,
                     1/L * (vC + vm2 - 2*vm1 + 2 * G * im1),
                     e * im1 - f * z1 + im1 * z1,
                     e * im2 - f * z2 + im2 * z2]
                    )

t = np.arange(0,100, 0.01)  # 时间序列 总共有 100/0.01=10000 个点
a = 0.5
b = 0.5
C = 0.1
e = 0.3
f = 1
G = 1.5
L = 0.4

par1 = [a, b, C, e, f, G, L]
P = odeint(dmove, (0.5, 0.1, 0.1, 0.1, 0.1), t, args=(par1,))
Im2 = (-1 * P[:, 0] - P[:, 2])
Vm1 = (b + a * P[:, 3]) * P[:, 2]
Vm2 = (b + a * P[:, 4]) * Im2
Pm1 = Vm1 * P[:, 2]
Pm2 = Vm2 * Im2

plt.figure()
plt.subplot(5, 1, 1)
plt.plot(P[:, 0], lw=0.7)
plt.ylabel("iL", fontsize=12)
plt.subplot(5, 1, 2)
plt.plot(P[:, 2], lw=0.7)
plt.ylabel("vC", fontsize=12)
plt.subplot(5, 1, 3)
plt.plot(P[:, 2], lw=0.7)
plt.ylabel("im1", fontsize=12)
plt.subplot(5, 1, 4)
plt.plot(P[:, 3], lw=0.7)
plt.ylabel("z1", fontsize=12)
plt.subplot(5, 1, 5)
plt.plot(P[:, 4], lw=0.7)
plt.xlabel("t/s", fontsize=12)
plt.ylabel("z2", fontsize=12)

plt.figure(figsize=(10, 6))
plt.subplot(1, 2, 1)
plt.plot(P[:, 2], Vm1, lw=0.8)
plt.xlabel("im1", fontsize=12)
plt.ylabel("Vm1", fontsize=12)
plt.subplot(1, 2, 2)
plt.plot(Im2, Vm2, lw=0.8)
plt.xlabel("im2", fontsize=12)
plt.ylabel("Vm2", fontsize=12)

plt.figure(figsize=(10, 6))
plt.subplot(1, 2, 1)
plt.plot(P[:, 2], Pm1, lw=0.8)
plt.xlabel("im1", fontsize=12)
plt.ylabel("Pm1", fontsize=12)
plt.subplot(1, 2, 2)
plt.plot(Im2, Pm2, lw=0.8)
plt.xlabel("im2", fontsize=12)
plt.ylabel("Pm2", fontsize=12)

plt.show()