CHAOTIC NN NOTE （二）2018-11-19

参考文献——对处于混沌状态的神经网络的控制

本文针对一种高阶、非对称和稀疏联结的hopfield型神经网络，利用控制混沌的著名方法——OGY方法，对处于混沌状态的网络进行控制，是网络的状态稳定在其演化方程的不稳定平衡点。

参考文献——control of chaos——a survey

1 parametric variation methods: the method of OGY control nonlinear system by stabilizing one of its unstable periodic orbits embedded in its chaotic attractor, via small time dependent perturbations of a variable system parameter. (not require any model equation for the nonlinear system, provided that a faithful nonlinear map )

参考文献——memristive neural network for on-line learning and tracking with brain-inspired spike timing dependent plasticity.

Demonstrate unsupervised learning and tracking in a spiking neural network with memristive synapses, weights are updated via brain-inspired spike timing dependent plasticity (STDP).
the synaptic conductance (突触传导系数) is up dated by the lacal time dependent superposition of pre- and post-synaptic spikes within a hybrid one-transistor/one-resistor memristive synapse. (突触状态只需高阻和低阻两种状态 sufficient to learn and recognize patterns.)
upscaling of software approaches is frustrated by the von Neumann architecture of conventional computing machines where the processor and memory units are physically separated. 断电后内存记忆丢失。A truly bio-realistic technology for neuromorphic systems (神经形态系统) requires a change of paradigm (范式) toward nonvolatile (非易丢失), multilevel (多级), and scalable (可扩展) synapses consistent with the ultra-high density of connections (一般一个神经元有10k个突触) in the human cortex. 三种记忆装置：resistive switching memory device, phase change memory devices, magneto resistive memory device (2-terminal structure)
neuromorphic ciruits with memristive synaptic arrays were experimentally evaluated by using recurrent Hopfield networks and perceptron networks (感知网络), showing pattern classification and supervised weight update via backpropagation or winner take all algorithms.
Neuromorphic circuits with memristive synaptic arrays were experimentally evaluated by using recurrent Hopfield networks.

参考文献——混沌控制综述_李卫东

混动控制方法：一是通过合适的方法使李雅普诺夫指数下降进而消除混沌。二是选择某一具有期望行为的轨道作为控制目标。
控制率的设计须最小限度改变原系统，从而对原系统的影响最小。从这个观点出发控制方式分为两类：反馈控制和非反馈控制。反馈控制的有点在于不需要使用除系统输出或状态以外的任何有关给定被控系统的信息，不改变被控系统的结构，具有良好的轨道跟踪能力和稳定性。其缺点在于要求一个比较精确的数学模型和输入目标函数或轨道，在只存在观测数据而没有数学方程时是无法直接使用的。非反馈控制：主要利用一个小的外部扰动（小的驱动信号，噪声信号，常量偏置、或系统参数的弱调制）来控制混沌。缺点是无法保证控制过程的稳定性。
混沌控制的常用方法：OGY方法（庞加莱截面：观测运动轨迹与此截面的截点( Poincare点)，设它们依次为P1,P2,P3…。原来相空间的连续轨迹在Poincare截面上便表现为一些离散点之间的映射Pn。由它们可得到关于运动特性的信息。如不考虑初始阶段的暂态过渡过程，只考虑Poincare截面的稳态图像，当Poincare截面上只有一个不动点和少数离散点时，可判定运动是周期的;当Poincare截面上是一封闭曲线时，可判定运动是准周期的;当Poincare截面上是成片的密集点，且有层次结构时，可判定运动处于混沌状态。），连续反馈控制法（外力反馈控制法：用强迫信号激励系统，并与响应信号比较，给出控制信号对系统微扰和延迟反馈控制法：利用系统响应的一部分并经时间延迟后，再与原来响应信号相减，其差值作为控制信号反馈到系统），自适应控制法（通过参量的调整来控制系统，调节是依靠目标输出与实际输出之间的信号来实现的）以及智能控制法（神经网络：使用神经网络方法镇定嵌入在不稳定混沌轨道中的吸引子，和模糊控制）等。（综述写作：引言，定义特点、方法介绍，小结方法优劣，发展方向）
混沌控制新方法：
1 通过改善混沌信号之间的空间关联性，混沌系统能以较快速度收敛到它的平衡点或多种周期轨道。
2 通过对混沌系统的适当分离，得到一个特殊的非线性函数，并利用混沌输出信号与其半周期延迟的非线性函数之和，构造了连续反馈输入干扰。

参考文献——混沌神经网络研究进展与展望_董军

混沌神经元研究中，振荡子（Oscillator）是一种典型的研究对象。混沌神经网络涉及联想记忆，组合优化。
混沌时间序列
研究间歇性（intermittency）有助于对混沌神经元及其网络的混沌动力学活动的本质进行了解。混沌在信息处理中，尤其是与联想记忆、模式识别有关的方面都有关心之处。
混沌神经网络模型：
aihara的混沌神经网络模型。（高亮部分）
inoue 等的混沌时间网络模型，用耦合的混沌振荡子作为单个神经元构造网络。同步异步对应神经元的激活和抑制两个状态。
耦合的混沌振荡子的同步来自规则性，而不规则性可产生随机搜索能力。

参考文献——联想记忆模型：Hopfield神经网络与动态神经网络_李耀勇博论文

1 hopfield网络要求记忆容量尽可能大，即记忆模式多。
2 容错好，噪声抵抗力强。
3 最好可以利用原来学习的信息来学习新的模式。
4 网络中不对应记忆模式的吸引点尽可能少。
5 网络的学习算法有生物学的依据。
6 一组模式能否被Hopfield网络记忆，归结于对应感知机所学习的模式组是否线性可分。

参考文献——Association memory realized by a reconfigurable memristive Hopfield neural network.（通过重组记忆Hopfield 网络实现联想记忆）

通过调整忆阻器阻值将不同的图形存储在记忆功能的Hopfield网络，同时预存好的图形也可直接或者通过一个联想中间态来恢复记忆。该网络对按内容访问存储器，旅行商推销员问题，组合优化问题很有效。早期Hopfield网络以高功耗芯片为代价，使用金属氧化物半导体做突触电路。该文使用二氧化铪HfO2。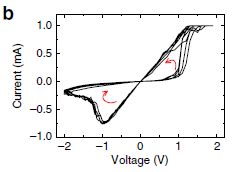
正电压增加导电系数，负电压减少导电系数，超过大电压（±2V）变化率增大。导电纤维模型内部氧空位的增加减少可以对此现象解释，氧空位浓度增加，忆阻器由高阻态转为低阻态。该文通过九个忆阻器来实现三个神经元与六个突触的记忆Hopfield网络。
如下图所示：

人工神经元拥有三个输入，同时每个输入对于一个权值w，输出表达式为：
$$y=sign(\sum _{i=1}^3{\omega }_i{N}_i-\theta )$$
θ是阀值，符号函数为0、1，

通过外部信号获得正负权值来控制S开关。权值为M/M+R，B直接传输信号，I为逆变器。

该图为由9个突触构成的三位记忆Hopfield神经网络，

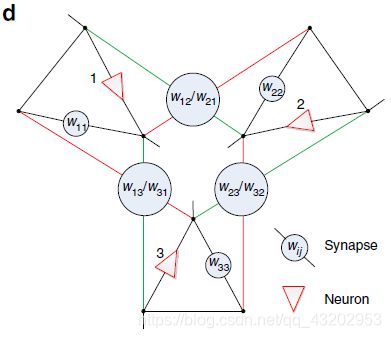
因权值对称，可用六个忆阻器实现该网络。
神经元状态更新函数为：
$$X(t+1)=sign(X(t)\ast W-T)$$
单联想记忆：联想记忆是人脑根据某片段信息回忆另一片段记忆的功能，在本文作者将一部分图片通过调整阻值矩阵获得期望权值来存储在MHN中，该权矩阵通过外积（Heb）规则进行优化，这里初始状态和最终状态的关系取决于权矩阵，阀值以及更新次序。

参考文献：Cascade chaotic system with application 2015

使用两个一维的混沌映射作为子映射，构造了一个串联混沌系统。该系统简称CCS，可产生大量新的混沌映射，新产生的混沌映射表现出更好的混沌特性，具有更多的参数，同时也是不可预测的特性。本文将CCS应用于可产生随机性更强的伪随机数发生器和高安全性能的数据加密系统。
常见的一维混沌映射：logistic map, tent map, gauss map, dyadic transformation.这些一维混沌映射具有优良的混沌特性，但安全缺陷也存在：混沌范围有限，参数个数少，输出可被预测。多维混沌映射模型至少有两个变量，例如：Henon map, Lorenz system, Chen and Lee system, hyperchaotic systems. 本文提出的两个一维混沌映射串联，第一个子映射的输出是第二子映射的输入，第二个子映射的输出反馈到第一个子映射的输入进行递归迭代，同时，第二个子映射的输出也是CCS系统的输出。
混沌映射from Wikipedia：Arnold tongue, Arnold’s cat map, Baker’s map, Complex quadratic map, Complex squaring map, Coupled map lattice, Double pendulum, Double scroll attractor, Duffing equation, Duffing map, Dyadic transformation, Dynamical billiards(outer), Exponential map, Gauss map, Gingerbreadman map, Hénon map, Horseshoe map, Ikeda map, Interval exchange map, Kaplan–Yorke map, Logistic map, Lorenz system, Multiscroll attractor, Rabinovich–Fabrikant equations, Rössler attractor, Standard map, Swinging Atwood’s machine, Tent map, Tinkerbell map, Van der Pol oscillator, Zaslavskii map.
本文通过李雅普诺夫指数分析CCS的混沌特性，首先通过假设初值并迭代得出T(X)的LE定义为

CCS的LE是其子映射LE的总和。
本文介绍了三种新混沌映射，Tent-logistic map, logistic-tent map and double-Sine map。LE值越大，输出轨迹的分岔速度越快。K熵是用来度量在单位时间内，预测一个动态系统轨道所平均需要的信息量。熵越大，说明动态系统越难以预测，混沌特性越好。

相关性测试：依据平均值和标准差。相关性小，则动态系统对初值及参数的变化灵敏。
本文依据上述新的混沌映射提出伪随机数发生器。

参考文献：Dynamic parameter control chaotic system 2016 (澳门大学)

动态参数控制混沌系统：使用控制映射（一个混沌映射）的输出调节子映射（另一个混沌映射）的参数。通过对比试验证明论文提出的映射在伪随机数发生器的应用具有良好的随机性。混沌最初是在气象学领域提出的概念。该文使用三种常用的混沌映射作为控制映射和子映射，对新的混沌系统进行了全面的理论分析，新方法可产生九种新的混沌映射，通过FPGA设计其中一种混沌映射，最后通过四种测试方法对利用新的动态混沌映射的PRNG进行评估。为满足参数范围，将控制映射的输出进行比例缩放。从三个方面分析DPCCS的李雅普诺夫指数，第一，控制映射的吸引子固定，即该映射产生一个固定的输出值，控制映射的李雅普诺夫指数等于系统的李雅普诺夫指数，第二，当吸引子是周期轨道（极限环）时，李雅普诺夫指数经推导写为：

第三，若吸引子为奇异吸引子时，其输出为动态不重复，则表现为良好的混沌特性。然后当子映射是连续的混沌范围，无论控制映射是否混沌，系统输出为混沌的，若子映射非连续范围，控制映射也不在混沌范围，则系统可能失去混沌特性。文章对比了九种CS的李雅普诺夫指数（正越大，越混沌），Kolmogorov熵（预测所需信息量），关联维数（吸引子奇异性，动态系统自由度），同时分析系统对初值的灵敏度。
硬件实现：FPGA、matlab

参考文献：chaos and dynamical systems Megan Richards

Baker map 有理数迭代后产生周期结果，无理数迭代后产生混沌特性，本文给出证明。
Lyapunov exponent determines whether or not a system is chaotic.
LE:
$$\lambda =\underset{n\to \infty }{\lim }\left\{\begin{array}{c}\frac{1}{n}{\sum }_{i=0}^{n-1}\ln \left|f^{\prime }(x_i)\right|\end{array}\right\}$$
If λ>0 we have chaotic dynamics.
Double pendulum. 此文章有部分编程案例可在必要时候参考。