MATLAB遗传算法解决旅行商（TSP）问题

二更：致所有想要学习这篇代码的同学

首先你得下载我上传过的数据集，解压后把他们跟程序放到一个目录下，否则连数据集都没有肯定会报错啊！如果你是自己下载的数据集，请把它保存成txt格式文件，内容修改成n行3列，第一列是序号，后两列是坐标；然后修改 set_data_set.m 使程序能读出你的数据集。这一步我相信只要是对MATLAB有些了解的同学应该都能完成。

另外，由于我的工作主要是复现了 Savuran Halil and Karakaya Murat. Route Optimization Method for Unmanned Air Vehicle Launched from a Carrier[J]. Lecture Notes on Software Engineering, 2015, 3(4) : 279-284. 因此如果想学习有关知识建议去读一下原始文献。

最后，时隔一年，我发现我的编程技巧和代码风格还亟需提高。请各位不要学习我这篇代码的代码风格，向其他高手看齐。最后祝各位学习顺利。

1 前言

这是一篇课程作业，目的是复现参考文献[1]，采用MATLAB编程。文献[1]用遗传算法解决了从直线运动运载体上发射的无人机的旅行商问题，本文对相关概念进行了介绍，给出了仿真程序与最终结果，并与文献[1]进行比较，验证了文献[1]的有效性。

至于为何要发博客，是因为这是我第一次完全看懂并从头到尾复现一篇文献的经历，特此纪念。请各位大佬轻喷，并希望在以后的生活学习中我能继续保持这种心态前进。写作中参考了其他博客与网页，如有侵权请联系我。

2 相关概念及原理

2.1 旅行商问题

旅行商问题（Travelling Salesman Problem, TSP）又称旅行推销员问题，是数学领域的著名问题之一。假设有一个旅行商人要拜访N个城市，每个城市只能拜访一次，而最后要回到原来的城市。旅行商问题的内容便是如何选择拜访城市的路线，使得总的路程最小。旅行商问题是一个NP问题，即非确定性多项式问题。它的解空间包含(N-1)!个方案，当N→∞时问题规模比指数级增长更快，当N大于一定程度时，采用穷举法求解旅行商问题的计算开销会变得不可接受。因此，解决旅行商问题多采用启发式算法，例如遗传算法、粒子群算法、蚁群算法、模拟退火算法等等。

2.2 遗传算法

遗传算法（Genetic Algorithm, GA）是由美国的John Holland于20世纪70年代提出，该算法根据自然界中的生物进化规律而设计。通过模拟自然选择和生物进化的遗传学机理，遗传算法是一种解决搜索问题的有效手段。遗传算法直接对某种结构对象进行操作，不存在求导与对函数连续性的要求，使用方便；遗传算法不是漫无目的的随机搜索，而是能自动获取、指导并优化搜索方向，因而具有更好的全局寻优能力。

遗传算法的基本单元是染色体。由于算法不能直接处理问题空间的参数，因此需要将待求解问题通过编码表示成遗传空间的染色体（或称个体），染色体中的每个单元称为基因。编码策略通常需要具备完备性、健全性和非冗余性。将问题编码后，就可以通过一定规则构建初始种群，随后便可开始进行进化模拟：

        （1）选择：模拟自然选择，从种群中通过某种特定规则选择出较适应环境的个体，适者生存，不适者淘汰，并用这些个体繁殖下一代。参照的规则由适应度函数表示，也可以用代价函数表示。

        （2）交叉：模拟生物繁殖过程中的染色体交叉互换。对两个不同的亲代个体在相同的位置进行基因交换，从而产生新的个体。

        （3）变异：模拟生物繁殖过程中的基因突变。随机选择种群中的某些个体，对其中的某些基因进行异向转化，从而保证基因的多样性。

每进行一周期遗传操作，产生的种群称作一代。在对每代染色体进行选择时可以采用精英主义，即大量克隆当前种群中的最优个体，保证最优个体的基因大概率会传播下去，从而在一定程度上杜绝遗传操作带来的退化现象。

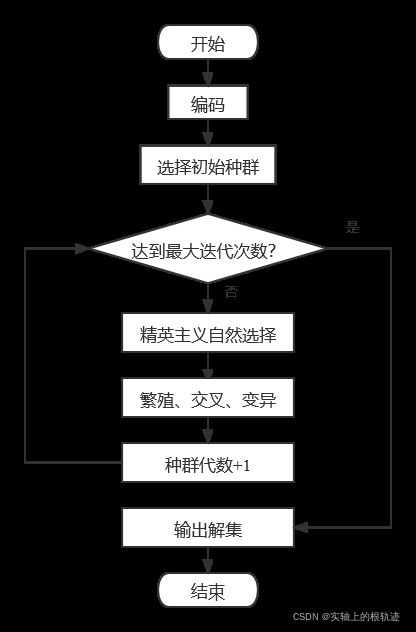
最后，本文遗传算法的步骤如图所示。

2.3 最邻近算法

另一个常用于解决TSP问题的算法是最邻近算法，其本质为贪心算法，即每一步都选择距离当前城市最近的城市作为下一个目的地。该方法的运算速度极快，但结果的好坏极大程度上取决于问题中各个城市点的排布。

2.4 2-Opt

2-Opt为2-Optimization的简称，即两元素优化。它是由Croes提出的，最早用于解决TSP问题的算法。2-Opt算法是一种局部搜索算法，其基本思路为：对于遗传空间中的一个可行解染色体，计算其代价，然后随机在染色体中选取两个基因位点，将两位点之间的染色体反转并接回原来的位置，并计算其代价。如果新染色体代价小于原染色体，则用新染色体代替原染色体，否则保持原染色体不变。从2-Opt的原理可知，只要给出足够长的时间，2-Opt必定能求出TSP问题的最优解。但实际上，由于基因位点选取的随机性和计算机计算能力的限制，2-Opt算法只能给出局部的最优解。这时，由于遗传算法具有全局寻优的能力，将遗传算法与2-Opt相结合能大大提高算法效果和效率。本文在每代遗传操作结束后用2-Opt方法处理种群所有染色体。

3 使用遗传算法解决TSP问题 

3.1 编码

对于旅行商问题，所要求解的是访问城市的最佳顺序。由于城市坐标已知，当顺序确定时，路程就确定了，据此可以将基因编码为正整数1,2,...,N，分别代表第1,2,...,N个城市，而城市访问顺序与染色体基因顺序一一对应。相应的适应度函数即为每条染色体所代表的访问顺序的总路程，总路程越低，说明适应能力越好。需要注意的是，适应度函数中也应该包括从起飞点到第一个城市，以及从最后一个城市到降落点的距离。

3.2 定义起飞点

出于简单考虑，本文假设运载体从原点(0,0)出发，并沿一个角度θ做速度为Vc的匀速直线运动。因此，运载体的路线是已知且可预测的，运载体路线上的所有点均可作为无人机的潜在起飞点。理论上，每个潜在起飞点之间的距离应足够小，才不会影响无人机的路径设计。在实验中，可以在运载体路线上取一定数量的等距点，近似作为起飞点参与TSP运算。更复杂的运载体运动路线可以以此为基础深入研究。

3.3 遗传操作

用遗传算法解决TSP问题的步骤与图1的流程大致相同，区别在于需要在“繁殖、交叉、变异”一步后加上2-Opt算法对本代染色体进行局部寻优。本文的算法设计流程如下：

       （1）初始化：将TSP中的地点次序编码成基因后，随机产生足够多的初代染色体加入种群，直到达到种群容量上限。对于起飞点，根据贪心算法的思想，将距离染色体首位基因所对应城市最近的潜在起飞点作为起飞点。

       （2）精英主义自然选择：将种群适应度从小到大排序，消灭后一半个体并克隆第一个个体，直到种群数量再次达到上限。这一步会保证当前的局部最优个体的基因大概率被传入子代中。

       （3）染色体交叉：由于TSP问题要求每个城市只访问一次，简单的染色体交叉可能会造成访问重复和空缺。为此采用部分映射交叉（Partial-Mapped Crossover, PMX）对染色体进行交叉处理。

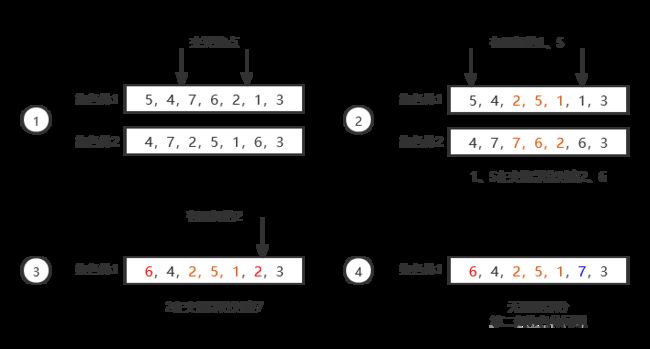
部分映射交叉的思想如下：首先随机选取两个交叉位点，交换两条亲代染色体在交叉位点之间的部分。然后固定交换的部分不变，遍历每条染色体中未交换的部分，如果有基因与交换部分重复，则根据交换部分的一一对应关系将重复的基因也换成相对的基因，如此往复直到每条染色体中都不包含重复的基因。部分交叉映射的一个例子如图所示：

        （4）基因突变：随机选取染色体中的两个位点，交换这两个位点的基因。

        （5）2-Opt：采用2-Opt算法对种群的每条染色体进行局部优化。在优化完成后，由于首位基因可能更改，所以需重新计算起飞点。

3.4 适应度计算

4 实验代码及仿真实验

4.1 实验代码

主函数main

%遗传算法解决旅行商问题
%参考文献
%Savuran Halil and Karakaya Murat.
%Route Optimization Method for Unmanned Air Vehicle Launched from a Carrier[J].
%Lecture Notes on Software Engineering, 2015, 3(4) : 279-284.
%——————————————————————————
%Copyright 2021 Eterrank. All rights reserved.

clear;clc;
%% 初始化
%初始化数据,读取数据集
UAV_SPEED = 300;                %无人机速度
CARRIER_SPEED = 40;             %运载体速度
CARRIER_THETA = pi/4;           %载体航向角
TAKEOFF_NUM = 30;               %起飞点数量设置
%读取数据集及参数配置
%共6个数据集，分别为'Berlin52','Eil76','Bier127'
%'CH130','CH150','KroB200'
DataCell = set_data_set('CH150');
GENES = DataCell{1};
POPSIZE = DataCell{2};          %种群大小
GENSIZE = DataCell{3};          %遗传代数
P_CROSS = DataCell{4};          %交叉概率
P_MUTATE = DataCell{5};         %变异概率
OPT_2 = DataCell{6};            %2-opt次数
t_factor = DataCell{7};         %地图尺度缩放因子，偷懒用
%% 绘制地图背景
%画出城市点
figure;plot(GENES(:,1),GENES(:,2),'.','markersize',10);
axis ij;    %反转坐标轴
%定义载体航线以及起飞点
%由于不同数据集地图大小不同，为了偷懒，用缩放因子t_factor放大缩小起飞点坐标
takeoff = zeros(TAKEOFF_NUM,2);
for i = 1:TAKEOFF_NUM
    takeoff(i,1) = i * CARRIER_SPEED * cos(CARRIER_THETA) * t_factor;
    takeoff(i,2) = i * CARRIER_SPEED * sin(CARRIER_THETA) * t_factor;
end
%% 初代遗传计算
%随机产生初始种群并指定起飞点，pop和takeoff_pos是索引
pop = generate(GENES,POPSIZE);
takeoff_pos = calc_takeoff_pos(GENES,pop,takeoff);
%检验每个城市对应的起飞点
% for i = 1:length(takeoff_pos)
%     hold on;
%     plot([GENES(pop(i,1),1),takeoff(takeoff_pos(i),1)],[GENES(pop(i,1),2),takeoff(takeoff_pos(i),2)]);
% end
%计算每条染色体的适应度，杀死后一半个体并克隆第一个个体
pop_after_clone = kill_clone(pop,takeoff_pos,GENES,takeoff,[]);
%部分映射交叉PMX、变异及精英主义筛选
pop_after_PMX = PMX(pop_after_clone,P_CROSS,P_MUTATE,GENES,takeoff);
%由于种群早已变化，重新计算一次起飞点
takeoff_pos = calc_takeoff_pos(GENES,pop_after_PMX,takeoff);
%2-opt局部最优搜索
new_pop = OPT2(pop_after_PMX,takeoff_pos,GENES,takeoff,OPT_2);
%再重新计算起飞点
takeoff_pos = calc_takeoff_pos(GENES,new_pop,takeoff);
%重新计算代价
value = cost(new_pop,takeoff_pos,GENES,takeoff);
%计算载体路程和降落点
[inter,r_val] = landing(new_pop,GENES,takeoff_pos,takeoff,value,UAV_SPEED,CARRIER_SPEED,CARRIER_THETA);
%计算总代价
value = value + r_val;
%% 子代循环计算
%至此初代计算完成，new_pop为子代，value为子代适应度，从杀死一半个体开始继续繁衍
%为防范变异影响，记录最后五代
[num,chromlength] = size(pop);
pop_5 = zeros(5,chromlength);
takeoff_5 = zeros(5,1);
value_5 = zeros(5,1);
inter_5 = zeros(5,2);           %最后五代的交汇点
%记录每轮最优代价值
value_all = zeros(GENSIZE,1);
for i = 1:GENSIZE
    pop_after_clone = kill_clone(new_pop,takeoff_pos,GENES,takeoff,value);
    pop_after_PMX = PMX(pop_after_clone,P_CROSS,P_MUTATE,GENES,takeoff);
    takeoff_pos = calc_takeoff_pos(GENES,pop_after_PMX,takeoff);
    new_pop = OPT2(pop_after_PMX,takeoff_pos,GENES,takeoff,OPT_2);
    takeoff_pos = calc_takeoff_pos(GENES,new_pop,takeoff);
    value = cost(new_pop,takeoff_pos,GENES,takeoff);
    [inter,r_val] = landing(new_pop,GENES,takeoff_pos,takeoff,value,UAV_SPEED,CARRIER_SPEED,CARRIER_THETA);
    value = value + r_val;
    [sort_val,index] = sort(value,'ascend');
    value_all(i) = sort_val(1);
    %防范变异影响，记录最后五代
    if i >= GENSIZE - 4
        j = i - GENSIZE + 5;
        pop_5(j,:) = new_pop(index(1),:);
        takeoff_5(j) = (takeoff_pos(index(1)));
        value_5(j) = sort_val(1);
        inter_5(j,:) = inter(index(1),:);
    end
end
%% 画图
%从最后五代中选择最优个体
[sort_val,index] = sort(value_5,'ascend');
chosen_one = pop_5(index(1),:);             %变量名瞎起的，天选之子chosen_one为最优染色体
his_takeoff = takeoff_pos(index(1));        %而他的起飞点是his_takeoff
%画路径，接着“绘制地图背景”中的figure继续画
hold on;plot(0:inter_5(index(1),1)/100:inter_5(index(1),1),0:inter_5(index(1),2)/100:inter_5(index(1),2),'--');
hold on;plot(takeoff(:,1),takeoff(:,2),'o');
hold on;plot([takeoff(his_takeoff,1),GENES(chosen_one(1),1)],...
    [takeoff(his_takeoff,2),GENES(chosen_one(1),2)]);
hold on;plot(GENES(chosen_one,1),GENES(chosen_one,2));
hold on;plot([GENES(chosen_one(chromlength),1),inter_5(index(1),1)],...
    [GENES(chosen_one(chromlength),2),inter_5(index(1),2)]);
hold on;plot(inter_5(index(1),1),inter_5(index(1),2),'rp');
xlabel('横坐标');ylabel('纵坐标');grid on;
title(['本次迭代最短路程为 ',num2str(sort_val(1))]);
figure;plot(1:GENSIZE,value_all);xlabel('代数');ylabel('代价（路程）');title('本次迭代中代价变化情况');grid on;
sort_val(1)         %输出最优代价
%%
%与最邻近算法比较
[val,t_o,N_inter] = NN(GENES,takeoff,UAV_SPEED,CARRIER_SPEED,CARRIER_THETA);
%绘制第x个起飞点的最邻近算法
[~,index] = sort(val,'ascend');
his_takeoff = index(1);
figure;plot(GENES(:,1),GENES(:,2),'.','markersize',10);axis ij;
hold on;plot(0:N_inter(his_takeoff,1)/500:N_inter(his_takeoff,1),0:N_inter(his_takeoff,2)/500:N_inter(his_takeoff,2),'--');
hold on;plot(takeoff(:,1),takeoff(:,2),'o');
hold on;plot([takeoff(his_takeoff,1),GENES(t_o(his_takeoff),1)],...
    [takeoff(his_takeoff,2),GENES(t_o(his_takeoff),2)]);
hold on;plot(GENES(t_o(his_takeoff,:),1),GENES(t_o(his_takeoff,:),2));
hold on;plot([GENES(t_o(his_takeoff,chromlength),1),N_inter(his_takeoff,1)],...
    [GENES(t_o(his_takeoff,chromlength),2),N_inter(his_takeoff,2)]);
hold on;plot(N_inter(his_takeoff,1),N_inter(his_takeoff,2),'rp');
xlabel('横坐标');ylabel('纵坐标');grid on;
title(['第 ',num2str(his_takeoff),'个起飞点最邻近路程为 ',num2str(val(his_takeoff))]);
min(val)            %输出最小代价

函数set_data_set，用于读取数据集

%遗传算法解决旅行商问题
%读取数据集并设定初始参数
%——————————————————————————
%Copyright 2021 Eterrank. All rights reserved.

function DataCell = set_data_set (str)
switch str
    case 'Berlin52'
        %Berlin52数据集
        GENES = importdata('Berlin52.txt');
        POPSIZE = 120;      %种群大小
        GENSIZE = 50;       %遗传代数
        P_CROSS = 1;        %交叉概率
        P_MUTATE = 0.5;     %变异概率
        OPT_2 = 20;         %2-opt次数
        t_factor = 1.2;     %缩放尺度因子
    case 'Eil76'
        %Eil76数据集
        GENES = importdata('Eil76.txt');
        GENES = GENES(:,2:3);
        POPSIZE = 120;      %种群大小
        GENSIZE = 80;       %遗传代数
        P_CROSS = 1;        %交叉概率
        P_MUTATE = 0.5;     %变异概率
        OPT_2 = 20;         %2-opt次数
        t_factor = 0.1;
    case 'Bier127'
        %Bier127数据集
        GENES = importdata('Bier127.txt');
        GENES = GENES(:,2:3);
        POPSIZE = 120;          %种群大小
        GENSIZE = 130;          %遗传代数
        P_CROSS = 1;            %交叉概率
        P_MUTATE = 0.5;         %变异概率
        OPT_2 = 20;             %2-opt次数
        t_factor = 18;
    case 'CH130'
        %CH130数据集
        GENES = importdata('CH130.txt');
        GENES = GENES(:,2:3);
        POPSIZE = 120;          %种群大小
        GENSIZE = 130;          %遗传代数
        P_CROSS = 1;            %交叉概率
        P_MUTATE = 0.5;         %变异概率
        OPT_2 = 20;             %2-opt次数
        t_factor = 0.7;
    case 'CH150'
        GENES = importdata('CH150.txt');
        GENES = GENES(:,2:3);
        POPSIZE = 120;          %种群大小
        GENSIZE = 150;          %遗传代数
        P_CROSS = 1;            %交叉概率
        P_MUTATE = 0.5;         %变异概率
        OPT_2 = 20;             %2-opt次数
        t_factor = 0.7;
    case 'KroB200'
        %KroB200数据集
        GENES = importdata('KroB200.txt');
        GENES = GENES(:,2:3);
        POPSIZE = 120;          %种群大小
        GENSIZE = 200;          %遗传代数
        P_CROSS = 1;            %交叉概率
        P_MUTATE = 0.5;         %变异概率
        OPT_2 = 20;             %2-opt次数
        t_factor = 3;
end
DataCell = {GENES,POPSIZE,GENSIZE,P_CROSS,P_MUTATE,OPT_2,t_factor};

函数generate，用于产生初始随机种群

%遗传算法解决旅行商问题
%随机产生初始种群
%输入基因genes，种群数量num
%输出num*chromlength的种群索引矩阵pop
%——————————————————————————
%Copyright 2021 Eterrank. All rights reserved.

function pop = generate(genes,num)
[chromlength,~] = size(genes);          %染色体长度
pop = zeros(num,chromlength);
for i = 1:num
    pop(i,:) = randperm(chromlength);   %随机全排列
end
end

函数calc_takeoff_pos，用于计算起飞点

%遗传算法解决旅行商问题
%计算起飞点
%输入基因genes，种群pop以及起飞点坐标矩阵takeoff
%输出起飞点索引列向量p
%——————————————————————————
%Copyright 2021 Eterrank. All rights reserved.

function p = calc_takeoff_pos(genes,pop,takeoff)
[num,~] = size(pop);        %num是种群大小POPSIZE
p = zeros(num,1);
for i = 1:num
    index = pop(i,1);       %第i个染色体的首个城市点坐标
    temp = zeros(length(takeoff),1);
    %用最邻近原则确定起飞点
    for j = 1:length(takeoff)
        temp(j) = sqrt((genes(index,1) - takeoff(j,1))^2 + (genes(index,2) - takeoff(j,2))^2);
    end
    [~,index] = min(temp);
    p(i) = index;
end
end

函数cost，用于计算代价

%遗传算法解决旅行商问题
%计算个体适应度（代价）
%方便起见并没有分得那么清，严格来说计算的是代价，适应度是代价的倒数
%输入城市坐标、起飞点坐标以及相应的索引
%返回与种群pop每行染色体一一对应的代价列向量value
%——————————————————————————
%Copyright 2021 Eterrank. All rights reserved.

function value = cost(pop,takeoff_pos,genes,takeoff)
[chromlength,~] = size(genes);          %染色体长度
num = length(takeoff_pos);              %种群大小
value = zeros(num,1);
for i = 1:num
    %遍历每个个体，将距离作为代价函数
    value(i) = 0;
    value(i) = value(i) + norm(takeoff(takeoff_pos(i),:) - genes(pop(i,1),:));
    for j = 1:chromlength - 1
        %计算染色体适应度
        value(i) = value(i) + norm(genes(pop(i,j),:) - genes(pop(i,j + 1),:));
    end
end
end
        

函数kill_clone，用于实现文章中的杀死后一半个体并克隆第一个个体

%遗传算法解决旅行商问题
%计算适应度后杀死后一半个体并克隆第一个个体
%也可以输入一个value直接排序，不进行适应度的重复计算
%——————————————————————————
%Copyright 2021 Eterrank. All rights reserved.

function pop = kill_clone(pop,takeoff_pos,genes,takeoff,given_value)
if (isempty(given_value))
    value = cost(pop,takeoff_pos,genes,takeoff);
else
    value = given_value;
end
[~,index] = sort(value,'ascend');           %升序排列
[num,~] = size(pop);
for i = fix(num/2):num
    pop(index(i),:) = pop(index(1),:);      %克隆最优个体填补后一半
end
end

函数PMX，用于实现染色体的交叉、变异及PMX操作

%遗传算法解决旅行商问题
%部分映射交叉PMX、变异与精英主义筛选
%——————————————————————————
%Copyright 2021 Eterrank. All rights reserved.

function new_pop = PMX(pop,p_cross,p_mutate,genes,takeoff)
[num,chromlength] = size(pop);
new_pop = zeros(num,chromlength);
count = 0;
while(count < num)
    count = count + 1;
    p = unifrnd(0,1);
    %满足概率才进行染色体交叉
    if p <= p_cross
        %随机选择两个亲代
        temp = randperm(num);       %用随机全排列的前两项来选择亲代
        parent_1_index = min(temp(1),temp(2));
        parent_2_index = max(temp(1),temp(2));
        parent_1 = pop(parent_1_index,:);
        parent_2 = pop(parent_2_index,:);
        %随机选择两个交叉点
        temp = randperm(chromlength);
        cross_1 = min(temp(1),temp(2));
        cross_2 = max(temp(1),temp(2));
        %交叉
        temp = parent_1(cross_1:cross_2);
        parent_1(cross_1:cross_2) = parent_2(cross_1:cross_2);
        parent_2(cross_1:cross_2) = temp;
        %部分映射交叉PMX
        flag = 1;
        while(flag)
            [temp,flag] = pmx_check(parent_1,parent_2,cross_1,cross_2);
            parent_1 = temp(1,:);
            parent_2 = temp(2,:);
        end
        %变异
        child_1 = mutate(parent_1,p_mutate);
        child_2 = mutate(parent_2,p_mutate);
        %计算子代适应度，择优选择
        pos_1 = calc_takeoff_pos(genes,child_1,takeoff);
        pos_2 = calc_takeoff_pos(genes,child_2,takeoff);
        val_1 = cost(child_1,pos_1,genes,takeoff);
        val_2 = cost(child_2,pos_2,genes,takeoff);
        if val_1 < val_2
            new_pop(count,:) = child_1;
        else
            new_pop(count,:) = child_2;
        end
    else
        %不满足概率直接变异
        child = mutate(pop(count,:),p_mutate);
        new_pop(count,:) = child;
    end
end
end

函数pmx_check，用于实现PMX中的映射替换

%遗传算法解决旅行商问题
%部分映射交叉PMX
%检查亲代交换后是否有重复，并进行映射替换
%——————————————————————————
%Copyright 2021 Eterrank. All rights reserved.

function [children,flag] = pmx_check(parent_1,parent_2,cross_1,cross_2)
flag = 0;
children = [];
for i = 1:length(parent_1)
    %跳过交叉部分
    if i>=cross_1&&i<=cross_2
        continue;
    else
        %按照映射交换重复部分
        for j = cross_1:cross_2
            if parent_1(i) == parent_1(j)
                parent_1(i) = parent_2(j);
                flag = 1;
            end
            if parent_2(i) == parent_2(j)
                parent_2(i) = parent_1(j);
                flag = 1;
            end
        end
    end
end
%返回两条经过PMX映射后的染色体
children = [children;parent_1];
children = [children;parent_2];
end

函数mutate，用于实现染色体的变异

%遗传算法解决旅行商问题
%变异
%——————————————————————————
%Copyright 2021 Eterrank. All rights reserved.

function children = mutate(parent,p_mutate)
p = unifrnd(0,1);
%不满足概率则不进行变异
if p > p_mutate
    children = parent;
    return;
end
%随机选择两点交换位置
temp = randperm(length(parent));
index_1 = temp(1);
index_2 = temp(2);
temp = parent(index_1);
parent(index_1) = parent(index_2);
parent(index_2) = temp;
children = parent;
end

函数OPT2，用于实现2-Opt操作

%遗传算法解决旅行商问题
%2-opt算法局部最优搜索
%——————————————————————————
%Copyright 2021 Eterrank. All rights reserved.

function new_pop = OPT2(pop,takeoff_pos,genes,takeoff,opt_num)
new_pop = pop;
[num,chromlength] = size(new_pop);
count = 0;
while (count < opt_num)
    count = count + 1;
    for i = 1:num
        %随机选择两个交叉点
        temp = randperm(chromlength);
        cross_1 = min(temp(1),temp(2));
        cross_2 = max(temp(1),temp(2));
        temp = new_pop(i,:);
        reverse_pop = [temp(1:cross_1 - 1),fliplr(temp(cross_1:cross_2)),temp(cross_2 + 1:chromlength)];
        reverse_pos = calc_takeoff_pos(genes,reverse_pop,takeoff);
        reverse_val = cost(reverse_pop,reverse_pos,genes,takeoff);
        val = cost(new_pop(i,:),takeoff_pos(i,:),genes,takeoff);
        if val >= reverse_val
            new_pop(i,:) = reverse_pop;
        end
    end
end
end

函数landing，用于计算降落点和降落阶段的代价

%遗传算法解决旅行商问题
%计算访问结束时载体所在位置inter以及回程代价r_val
%由于题目限制，应该只能计算直线
%经验算，用速度预测和用三角函数算出的距离误差量级在1e-10左右，效果良好
%——————————————————————————
%Copyright 2021 Eterrank. All rights reserved.

function [inter,r_val] = landing(pop,genes,takeoff_pos,takeoff,value,u_speed,c_speed,c_theta)
[num,chromlength] = size(pop);
fly_time = zeros(num,1);
carrier_pos = zeros(num,2);
for i = 1:num
    fly_time(i) = value(i)/u_speed;
    carrier_pos(i,:) = [takeoff(takeoff_pos(i),1) + c_speed * fly_time(i) * cos(c_theta),...
        takeoff(takeoff_pos(i),2) + c_speed * fly_time(i) * sin(c_theta)];
end
%显示结束时载体位置
% hold on;plot(carrier_pos(:,1),carrier_pos(:,2),'o');
%获取结束时无人机位置
temp = pop(:,chromlength);
last_location = genes(temp,:);
%计算无人机和载体的交汇点
intersection_p = zeros(num,2);
return_value = zeros(num,1);
for i = 1:num
    vec_1 = carrier_pos(i,:);           %载体航向向量
    vec_2 = last_location(i,:) - carrier_pos(i,:);      %载体初始位置指向无人机的向量
    vec_Theta = acos(dot(vec_1,vec_2)/norm(vec_1)/norm(vec_2));
    sin_alpha = c_speed / u_speed * sin(vec_Theta);
    alpha = asin(sin_alpha);
    if alpha < 0
        alpha = alpha + pi;
    end
    beta = pi - alpha - vec_Theta;          %内角和180°
    %求出载体继续行进的距离
    dist = norm(carrier_pos(i,:) - last_location(i,:));
    x = dist * sin(alpha) / sin(beta);
    %求出交汇点
    intersection_p(i,:) = [carrier_pos(i,1) + x * cos(c_theta),carrier_pos(i,2) + x * sin(c_theta)];
    %记录返回路程
    t = x/c_speed;
    return_value(i) = t * u_speed;
end
inter = intersection_p;
r_val = return_value;
end

函数NN，用于实现最邻近算法求解本问题

%遗传算法解决旅行商问题
%与最邻近算法比较
%——————————————————————————
%Copyright 2021 Eterrank. All rights reserved.

function [val,takeoff_out,inter] = NN(genes,takeoff,u_speed,c_speed,c_theta)
[chromlength,~] = size(genes);          %染色体长度
[takeoff_num,~] = size(takeoff);        %起飞点个数
temp = 1:chromlength;temp = temp';
genes_c = [temp,genes,zeros(chromlength,1)];        %广义染色体变量，一维为序号，四维为访问标识
val = zeros(takeoff_num,1);
takeoff_out = zeros(takeoff_num,chromlength);
for i = 1:takeoff_num
    temp_val = zeros(chromlength,1);
    %先计算从起飞点到第一个城市
    for j = 1:chromlength
        temp_val(j) = temp_val(j) + norm(takeoff(i,:) - genes(j,:));
    end
    [sort_val,index] = sort(temp_val,'ascend');
    val(i) = val(i) + sort_val(1);
    takeoff_out(i,1) = index(1);
    genes_c(index(1),4) = 1;        %将访问标识置1
    %再计算之后的城市
    cur_pos = genes(index(1),:);
    for j = 1:chromlength - 1
        temp_val = zeros(chromlength,1);
        %计算到所有未访问点的距离
        for k = 1:chromlength
            if genes_c(k,4) == 1
                temp_val(k) = 10e12;
                continue;
            else
                temp_val(k) = temp_val(k) + norm(cur_pos - genes(k,:));
            end
        end
        [sort_val,index] = sort(temp_val,'ascend');
        val(i) = val(i) + sort_val(1);
        takeoff_out(i,j + 1) = index(1);
        genes_c(index(1),4) = 1;        %将访问标识置1
        cur_pos = genes(index(1),:);
    end
    genes_c(:,4) = zeros(chromlength,1);
end
%至此最邻近路线分配完毕，应该没有问题
%计算着陆点
fly_time = zeros(takeoff_num,1);
carrier_pos = zeros(takeoff_num,2);
for i = 1:takeoff_num
    fly_time(i) = val(i)/u_speed;
    carrier_pos(i,:) = [takeoff(i,1) + c_speed * fly_time(i) * cos(c_theta),...
        takeoff(i,2) + c_speed * fly_time(i) * sin(c_theta)];
end
temp = takeoff_out(:,chromlength);
last_location = genes(temp,:);
intersection_p = zeros(takeoff_num,2);
return_value = zeros(takeoff_num,1);
for i = 1:takeoff_num
    vec_1 = carrier_pos(i,:);           %载体航向向量
    vec_2 = last_location(i,:) - carrier_pos(i,:);      %载体初始位置指向无人机的向量
    vec_Theta = acos(dot(vec_1,vec_2)/norm(vec_1)/norm(vec_2));
    sin_alpha = c_speed / u_speed * sin(vec_Theta);
    alpha = asin(sin_alpha);
    if alpha < 0
        alpha = alpha + pi;
    end
    beta = pi - alpha - vec_Theta;          %内角和180°
    %求出载体继续行进的距离
    dist = norm(carrier_pos(i,:) - last_location(i,:));
    x = dist * sin(alpha) / sin(beta);
    %求出交汇点
    intersection_p(i,:) = [carrier_pos(i,1) + x * cos(c_theta),carrier_pos(i,2) + x * sin(c_theta)];
    %记录返回路程
    t = x/c_speed;
    return_value(i) = t * u_speed;
end
inter = intersection_p;
val = val + return_value;
end

4.2 仿真结果

采用常用的TSP数据集对遗传算法和最邻近算法的结果进行仿真验证。

数据集	节点数	已知最优路程长度
Berlin52	52	7542
Eil76	76	538
Bier127	127	118282
Ch130	130	6110
Ch150	150	6528
KroB200	200	29437

需注意，表中所列的最优路程长度为静态TSP问题的最优路程长度，因此本文所做的仿真结果会与其存在差异。假设无人机与运载体均为匀速，所使用的参数如下：

无人机速度	运载体速度	潜在起飞点数量
300	40	30

需注意，文献[1]中选用的起飞点数量为24。本文为了更好的仿真效果，将起飞点数量选为30。由于起飞点只影响第一段路程，起飞点数量的变化对结果产生的影响较小。

对每个数据集，所使用的遗传算法参数如下：

数据集	种群数量上限	遗传代数	交叉概率	突变概率
Berlin52	120	50	1.0	0.5
Eil76	120	80	1.0	0.5
Bier127	120	130	1.0	0.5
Ch130	120	130	1.0	0.5
Ch150	120	150	1.0	0.5
KroB200	120	200	1.0	0.5

由于遗传算法的随机性，需要多次运行算法进行验证。文献[1]中对每个数据集运行了30次遗传算法程序。本文限于实验设备的性能，只对每个数据集运行了10次算法程序。可以观察到，所有程序均在有限的次数内收敛到了稳定值。作为对比，下面给出Berlin52和Bier127数据集某次实验的收敛曲线。

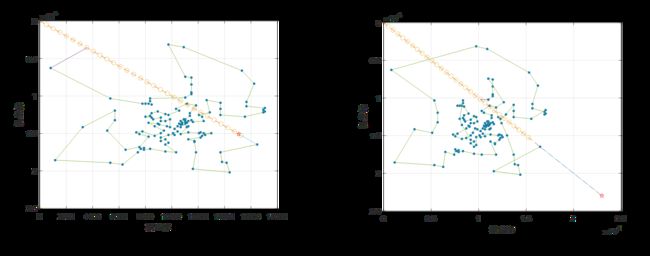
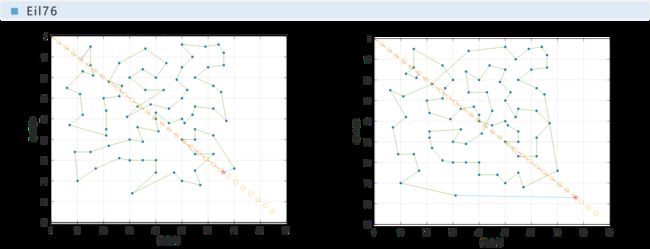
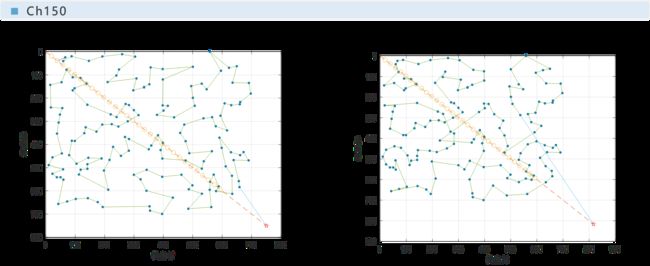
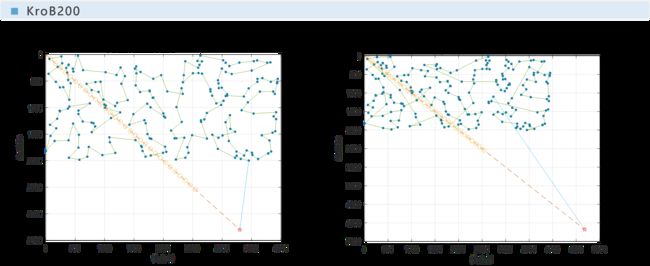
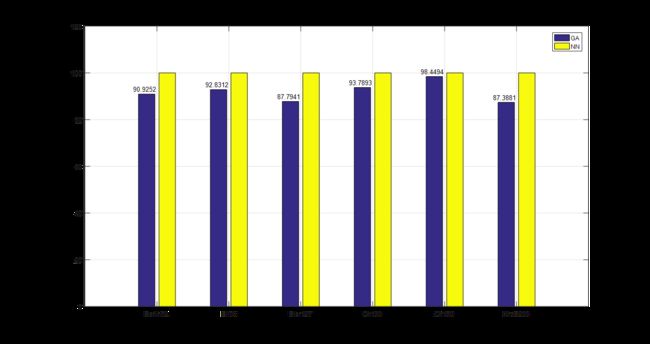
下面给出本文与文献[1]所给的例子的对比情况，并采用百分比柱状图对遗传算法与最邻近算法的效率进行对比。

 

 

实验表明，遗传算法是收敛的，且在遗传代数达到一半之前就几乎已经收敛完全。

从对比图中可以看出，遗传算法的运算结果比最邻近算法更优，最高可达最邻近算法的87%，即可节省路程13%；文献[1]中最终结果为最高可节省18%。

本文与文献[1]的结果存在差异。除了遗传算法带来的随机性差异之外，差异的原因还可能有两点：

       （1）起飞点的选择：文献[1]中未给出起飞点选择的方案，且选择数量和夹角与本文不同。实验表明，起飞点选取的间隔与路线夹角对实验结果有较大影响，这有可能是造成差异的主要原因之一。

       （2）2-Opt算法的次数：由于2-Opt算法在次数趋于无穷时会收敛到最优解，但由于机器性能限制，本文试验对每代遗传只进行20次2-Opt优化，这可能导致可行解收敛在一个次优解附近，且这个次优解足够优秀以至于遗传算法在有限次迭代内无法使其跳出。这也有可能是导致本文与文献[1]结果相差较大的原因之一。

5 结论

本文研究并复现了文献[1]，提出了一种基于遗传算法的无人机航路规划优化方法，研究的主要内容是在TSP路径规划中动态地包含无人机的起降点，并计算总路程来判断方法的优劣。随后，将遗传算法与最邻近算法的仿真结果进行比较，结果表明遗传算法结果更优，相较于最邻近算法平均能节省约91.8629%的路程。最后，对本文与文献[1]的结果差异进行了分析。

参考文献

[1] Savuran Halil and Karakaya Murat. Route Optimization Method for Unmanned Air Vehicle Launched from a Carrier[J]. Lecture Notes on Software Engineering, 2015, 3(4) : 279-284.