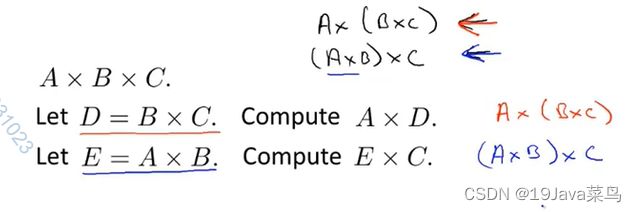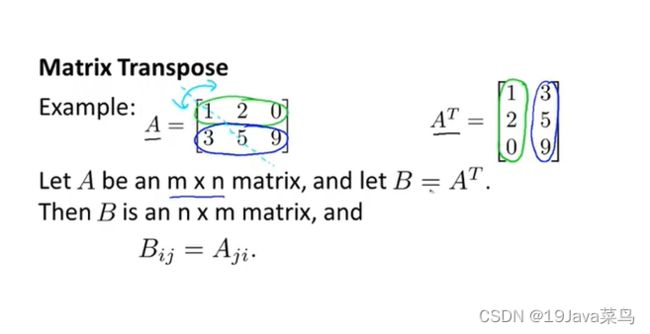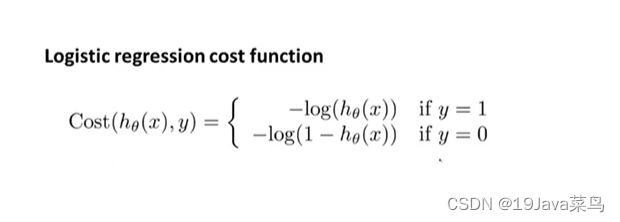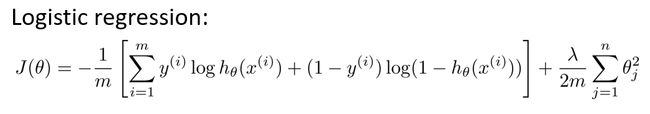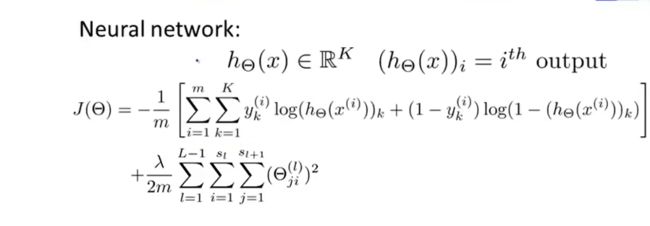【Machine Learning】机器学习笔记-(上半部分)
初识机器学习
文章目录
- 初识机器学习
- 一,机器学习
- - 1. 机器学习定义
- - 2. 机器学习算法分类
-
- - 1.2.1 监督学习定义
- - 1.2.2 回归问题
- - 1.2.3分类问题
- - 1.3 无监督学习
-
- - 1.3.1 无监督学习定义
- - 1.3.2 聚类算法
- 二,单变量线性回归
- - 2.1 单变量线性回归函数
- - 2.2 平方误差函数(代价函数)
-
- - 2.2.1只考虑 θ 1 θ_1 θ1的代价函数
- - 2.2.2 θ 0 θ_0 θ0, θ 1 θ_1 θ1都考虑的代价函数
- - 2.3梯度下降
- - 2.4Batch梯度下降
- 三,矩阵
- - 3.1矩阵和向量
- - 3.2加法和标量乘法
- - 3.3矩阵向量乘法
- - 3.4矩阵乘法
- - 3.5矩阵乘法特征
- - 3.6逆和转置
- 四,多变量线性回归
- -4.1多变量线性回归假设函数
- -4.2多元梯度下降法
-
- -4.2.1特征缩放
- -4.2.2学习率
- -4.3特征和多项式回归
- -4.4正规方程
-
- -4.4.1正规方程推导
- -4.4.2正规方程在矩阵不可逆情况解决方案
- 五,逻辑回归
- -5.1分类问题
- -5.2假设陈述
- -5.3决策边界
- -5.4代价函数
-
- -5.4.1代价函数推导
- -5.4.2简化代价函数和梯度下降
- -5.5高级优化
- -5.6多元分类:一对多
- 六,正则化
- -6.1 过拟合问题
- -6.2 过拟合代价函数
- -6.3 线性回归的正则化
- -6.4 逻辑回归的正则化
- 七,神经网络
- -7.1 非线性假设
- -7.2 神经元与大脑
- -7.3 模型展示
- -7.4 例子与直觉理解
- -7.5 多元分类
- 八,神经网络应用
- -8.1 代价函数
- -8.2 反向传播算法
- -8.3 理解反向传播算法
- -8.4 使用注意:展开参数
- -8.5 梯度检测
- -8.6 随机初始化
- -8.7 组合到一起
- -8.8 无人驾驶
一,机器学习
- 1. 机器学习定义
计算机程序从经验E中学习,解决某一任务T,进行某一性能P,通过P测定在T上的表现因经验E而提高(Tom`s definition)
例1:对于跳棋程序中
E: 程序自身下的上万盘棋局
T:下跳棋
P:与新对手下跳棋时赢的概率
例2:对于识别垃圾邮件程序中
E:观察你标记邮件
T:区分邮件是否是垃圾邮件
P:正确区分垃圾邮件的比率
- 2. 机器学习算法分类
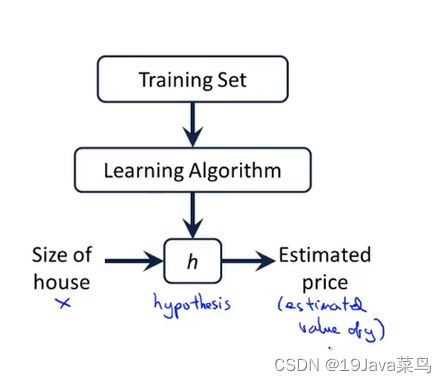
按照学习方法不同,最主要的两类是监督学习和无监督学习
- 1.2.1 监督学习定义
给算法一个数据集,其中包含了正确答案,算法的目的是给出更多的正确答案
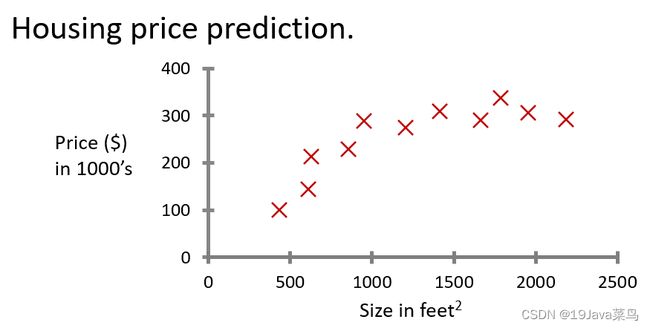
- 1.2.2 回归问题
例2:假设你有几千件衣服要去卖,预测一下未来三个月内你可以卖出去多少件衣服
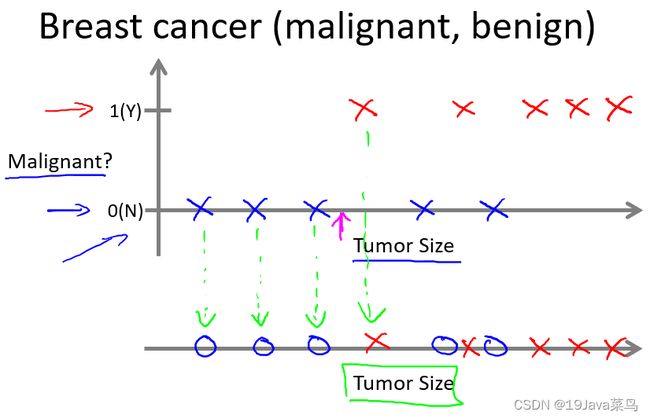
- 1.2.3分类问题
算法最终的目的是解决无穷多个特征的数据集
分类问题目的: 预测离散值输出。
就本问题而言,结果只有0和1的输出。
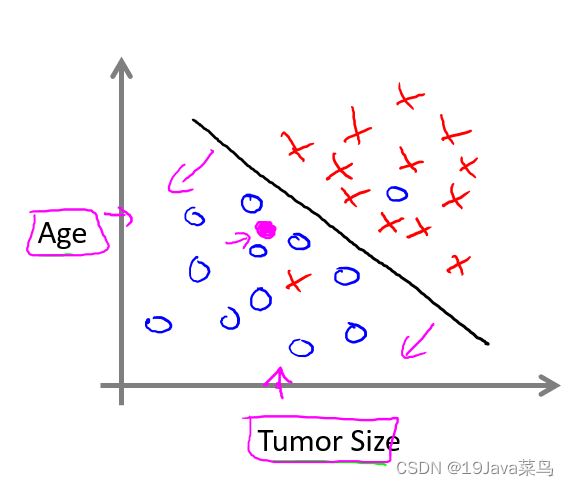
例2:你有很多用户,你想写一个软件来检查每一个用户的账户,对于每一个用户,判断这个用户是否被入侵或破坏
- 1.3 无监督学习
- 1.3.1 无监督学习定义
只给算法一个数据集,但是不给数据集的正确答案,由算法自行分类。
- 1.3.2 聚类算法
聚类算法可以根据已有数据把数据分成不同的簇
例2:谷歌新闻按照主题分类
例3:市场通过对用户进行分类,确定目标用户
例4:鸡尾酒算法:两个麦克风分别离两个人不同距离,录制两段录音,将两个人的声音分离开来(只需一行代码就可实现,但实现的过程要花大量的时间)
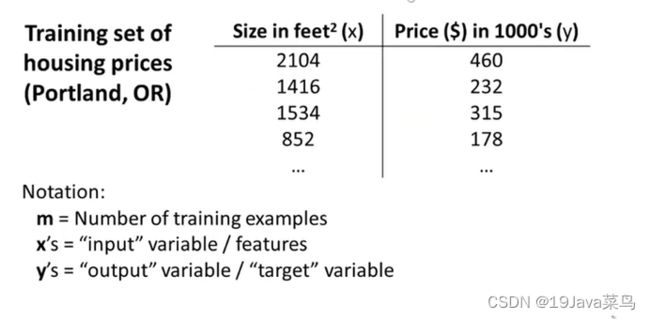
二,单变量线性回归
- 2.1 单变量线性回归函数
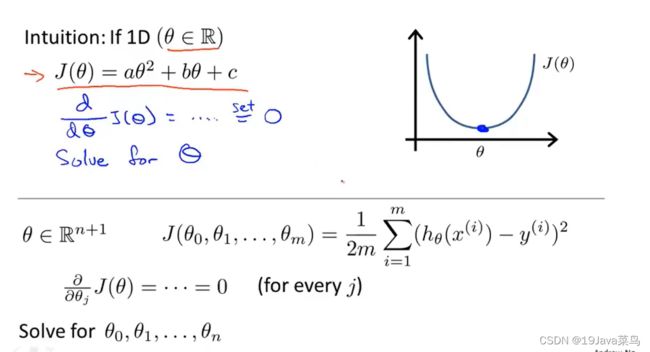
单变量线性回归假设函数: h θ ( x ) = θ 0 + θ 1 x h_θ(x) = θ_0 + θ_1x hθ(x)=θ0+θ1x
- 2.2 平方误差函数(代价函数)
代价函数: J ( θ 0 , θ 1 ) = 1 2 m ∑ i = 1 n ( h ( x ( i ) ) − y ( i ) ) 2 J(θ_0,θ_1)=\frac{1}{2m}\sum_{i=1}^n(h(x^{(i)})-y^{(i)})^2 J(θ0,θ1)=2m1∑i=1n(h(x(i))−y(i))2 (m表示训练样本的数量)
重新复习补充: h ( x ( i ) ) h(x^{(i)}) h(x(i))是预测值, y ( i ) y^{(i)} y(i)是实际值,两者取差。公式中的这个平方,似乎是最小二乘法和最佳平方/函数逼近,涉及到数值分析这一块知识,前置知识太多没去细理解,先按方差这么去理解。至于前面的 1 2 m \frac{1}{2m} 2m1中的2是为了后续求偏导更好计算。
目标: 最小化代价函数,即minimize J ( θ 0 , θ 1 ) J(θ_0,θ_1) J(θ0,θ1)
代价函数也被称为平方误差函数或者平方误差代价函数,在线性回归问题中,平方误差函数是最常用的手段
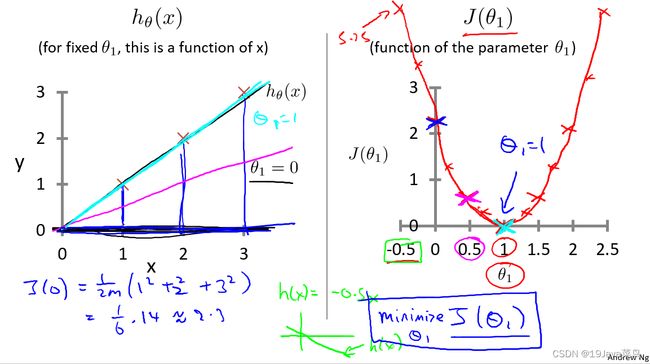
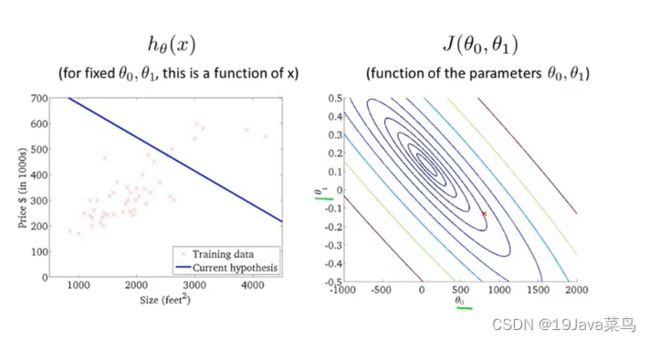
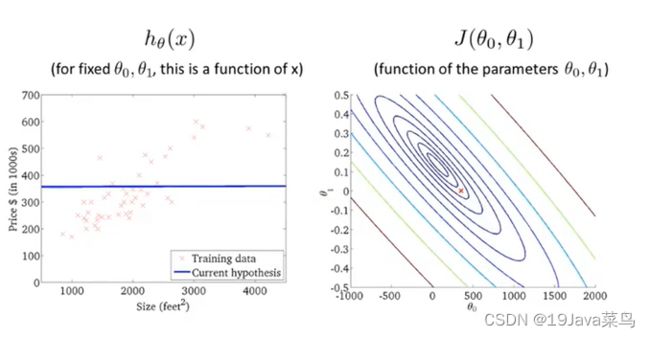
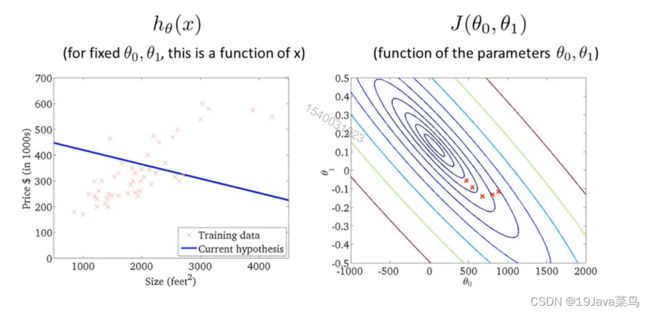
- 2.2.1只考虑 θ 1 θ_1 θ1的代价函数
代价函数模型
为方便分析,先取 θ 0 θ_0 θ0=0并改变 θ 1 θ_1 θ1的值,得到多组 J ( θ 1 ) = 1 2 m ∑ i = 1 n ( h ( x ( i ) ) − y ( i ) ) 2 J(θ_1)=\frac{1}{2m}\sum_{i=1}^n(h(x^{(i)})-y^{(i)})^2 J(θ1)=2m1∑i=1n(h(x(i))−y(i))2 如右图
给定训练集为(1,1),(2,2),(3,3), h θ ( x ) h_θ(x) hθ(x)模型如下
此时作出假设函数的图像如右图
得到的minimize J(θ0) 就是线性回归的目标函数
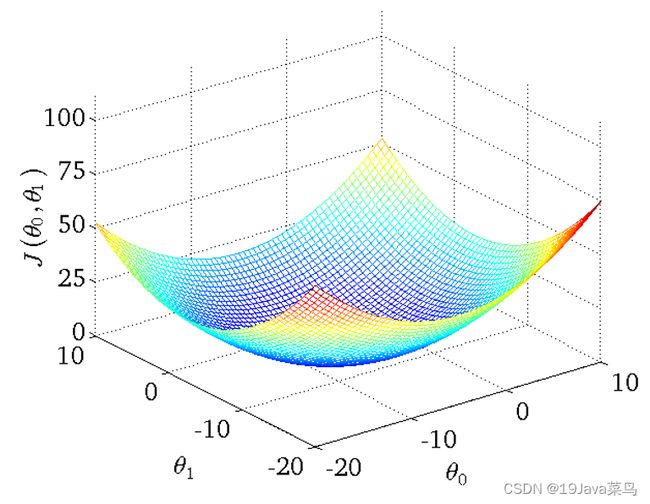
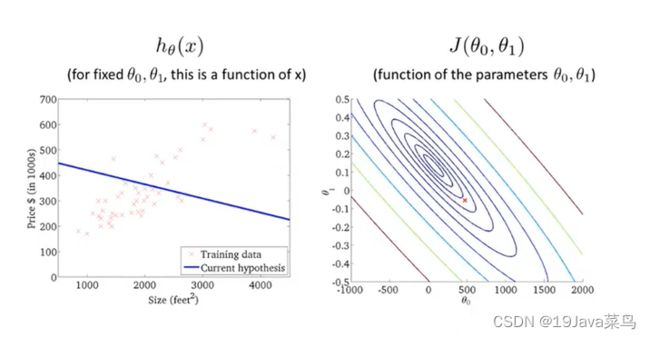
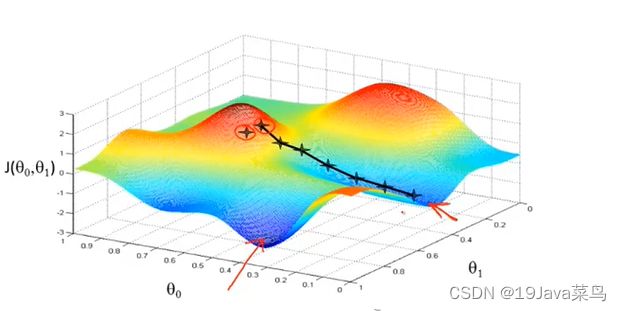
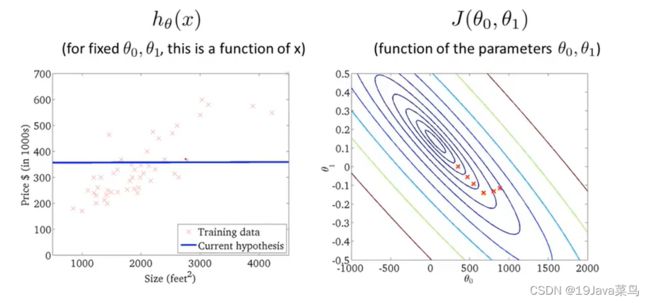
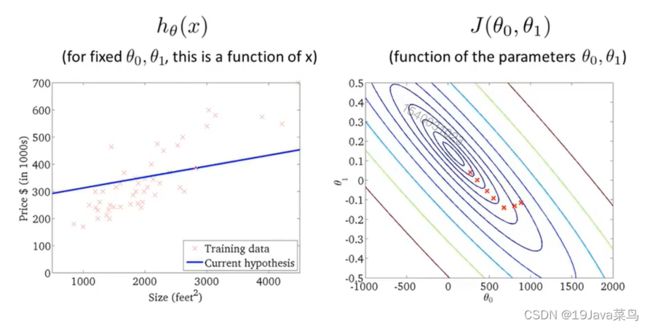
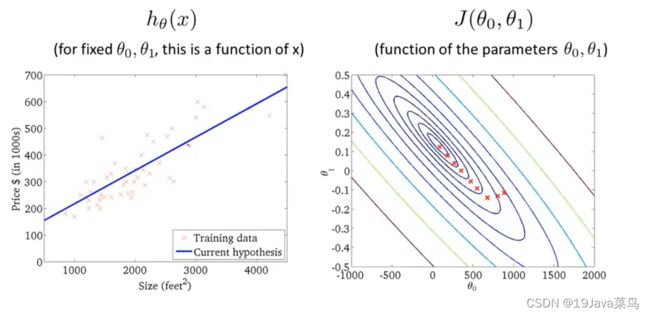
- 2.2.2 θ 0 θ_0 θ0, θ 1 θ_1 θ1都考虑的代价函数
代价函数模型
此时给定的训练集如下
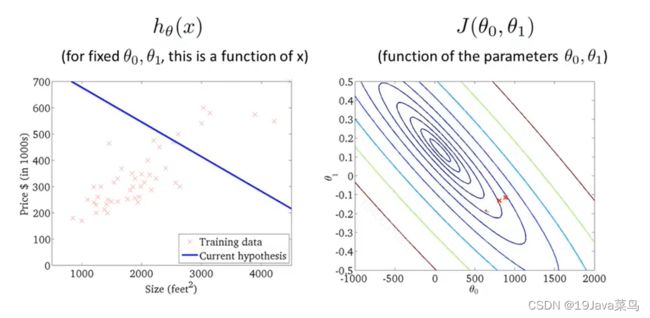
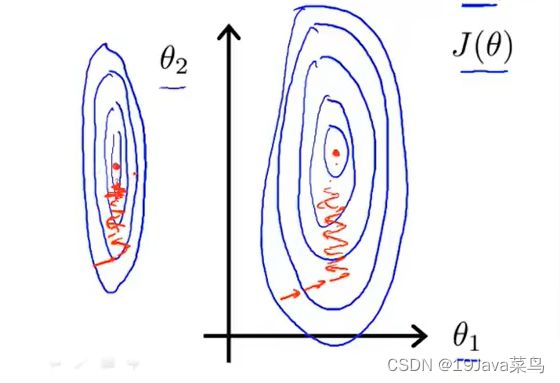
绘制代价函数得到如下三维图
用等高图像表示代价函数和假设函数的关系
其中,等高线的中心对应最小代价函数
观测方法:观察等高线的中心对应的 θ 0 θ_0 θ0, θ 1 θ_1 θ1与我们假设函数的 θ 0 θ_0 θ0, θ 1 θ_1 θ1是否一致即可
如果有更高维的图像,更多的参数,那我们将无法画出图像
所以我们需要的是自动找寻代价函数J( θ 0 θ_0 θ0, θ 1 θ_1 θ1)最小值对应的 θ 0 θ_0 θ0, θ 1 θ_1 θ1
而不是只能画出图形然后手动读取方法.
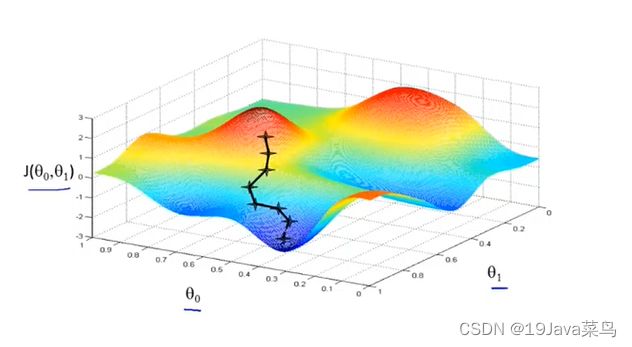
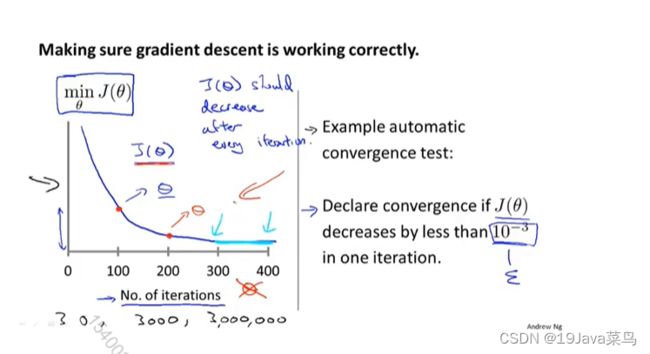
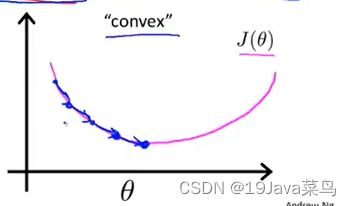
- 2.3梯度下降
算法思想
- 指定 θ 0 θ_0 θ0, θ 1 θ_1 θ1的初始值
- 不断改变 θ 0 θ_0 θ0, θ 1 θ_1 θ1的值,使J( θ 0 θ_0 θ0, θ 1 θ_1 θ1)不断减小
- 得到一个最小值或局部最小值时停止
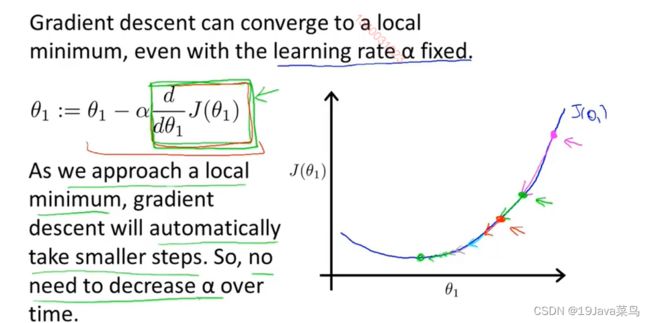
梯度: 函数中某一点(x, y)的梯度代表函数在该点变化最快的方向
(选用不同的点开始可能达到另一个局部最小值)
梯度下降算法
符号解释
:=代表赋值,如a:=b代表把b的值赋给a
=代表判断,如a=b代表a与b是否相等
α \alpha α代表’‘下山’‘步伐的大小
∂ ∂ θ 0 J ( θ 0 , θ 1 ) \frac{\partial }{\partial θ_0} J(θ_0,θ_1) ∂θ0∂J(θ0,θ1)代表行走的’‘方向’’
梯度下降公式
θ j = θ j − α ⋅ ∂ ∂ θ 0 J ( θ 0 , θ 1 ) θ_j=θ_j-\alpha·\frac{\partial }{\partial θ_0} J(θ_0,θ_1) θj=θj−α⋅∂θ0∂J(θ0,θ1)
其中 α \alpha α是学习速率
θ 0 和 θ 1 θ_0和θ_1 θ0和θ1应同步更新,否则如果先更新 θ 0 θ_0 θ0,会使得 θ 1 θ_1 θ1是根据更新后的 θ 0 θ_0 θ0去更新的,与正确结果不相符
∂ ∂ θ 0 J ( θ 0 , θ 1 ) \frac{\partial }{\partial θ_0} J(θ_0,θ_1) ∂θ0∂J(θ0,θ1)方向问题
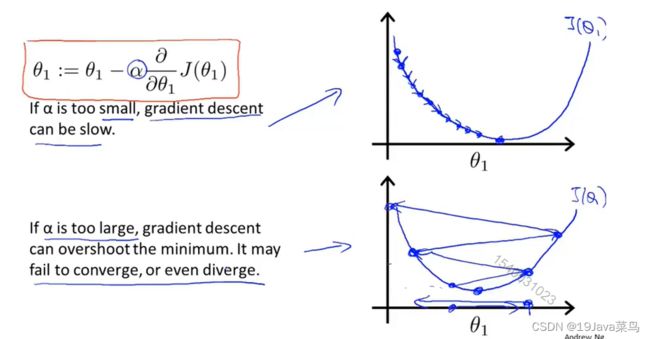
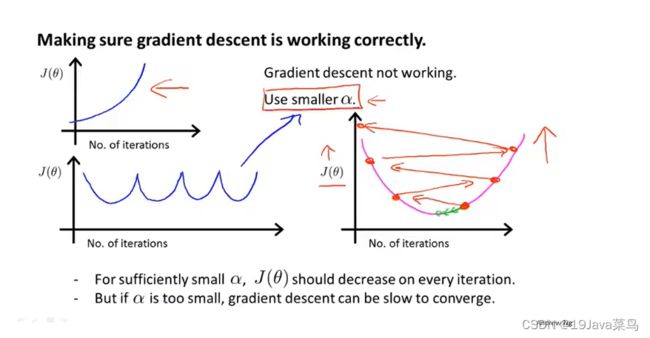
α \alpha α大小问题
如果α选择太小,会导致每次移动的步幅都很小,最终需要很多步才能最终收敛
如果α选择太大,会导致每次移动的步幅过大,可能会越过最小值,无法收敛甚至会发散
- 2.4Batch梯度下降
公式推导
J ( θ 0 , θ 1 ) = 1 2 m ∑ i = 1 n ( h ( x ( i ) ) − y ( i ) ) 2 = 1 2 m ∑ i = 1 n ( θ 0 + θ 1 x ( i ) − y ( i ) ) 2 J(θ_0,θ_1)=\frac{1}{2m}\sum_{i=1}^n(h(x^{(i)})-y^{(i)})^2=\frac{1}{2m}\sum_{i=1}^n(θ_0+θ_1x^{(i)}-y^{(i)})^2 J(θ0,θ1)=2m1∑i=1n(h(x(i))−y(i))2=2m1∑i=1n(θ0+θ1x(i)−y(i))2
j = 0时表示对 θ 0 θ_0 θ0求偏导
j = 1时表示对 θ 1 θ_1 θ1求偏导
∂ ∂ θ 0 J ( θ 0 , θ 1 ) = 1 2 m ∑ i = 1 n ( h θ ( x ( i ) ) − y ( i ) ) \frac{\partial }{\partial θ_0} J(θ_0,θ_1)=\frac{1}{2m}\sum_{i=1}^n(h_θ(x^{(i)})-y^{(i)}) ∂θ0∂J(θ0,θ1)=2m1∑i=1n(hθ(x(i))−y(i))
∂ ∂ θ 1 J ( θ 0 , θ 1 ) = 1 2 m ∑ i = 1 n ( h θ ( x ( i ) ) − y ( i ) ) ⋅ x ( i ) \frac{\partial }{\partial θ_1} J(θ_0,θ_1)=\frac{1}{2m}\sum_{i=1}^n(h_θ(x^{(i)})-y^{(i)})·x^{(i)} ∂θ1∂J(θ0,θ1)=2m1∑i=1n(hθ(x(i))−y(i))⋅x(i)
x ( i ) x^{(i)} x(i)表示第i个样本
进而得
θ 0 : = θ 0 − α ⋅ 1 m ∑ i = 1 n ( h θ ( x ( i ) ) − y ( i ) ) θ_0:=θ_0-\alpha·\frac{1}{m}\sum_{i=1}^n(h_θ(x^{(i)})-y^{(i)}) θ0:=θ0−α⋅m1∑i=1n(hθ(x(i))−y(i))
θ 1 : = θ 1 − α ⋅ 1 m ∑ i = 1 n ( h θ ( x ( i ) ) − y ( i ) ) ⋅ x ( i ) θ_1:=θ_1-\alpha·\frac{1}{m}\sum_{i=1}^n(h_θ(x^{(i)})-y^{(i)})·x^{(i)} θ1:=θ1−α⋅m1∑i=1n(hθ(x(i))−y(i))⋅x(i)
线性回归的梯度下降的函数是凸函数,因此没有局部最优解,只有全局最优解
例
三,矩阵
- 3.1矩阵和向量
- 3.2加法和标量乘法
- 3.3矩阵向量乘法
- 3.4矩阵乘法
- 3.5矩阵乘法特征
- 3.6逆和转置
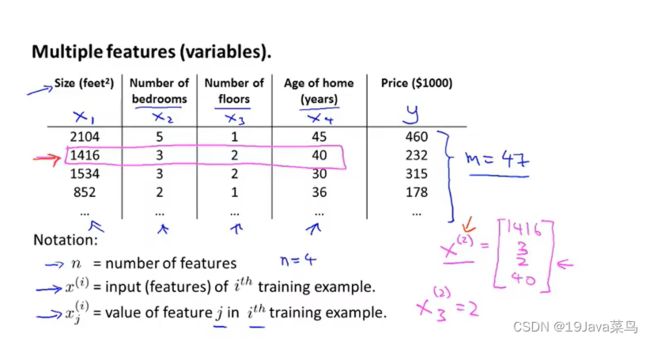
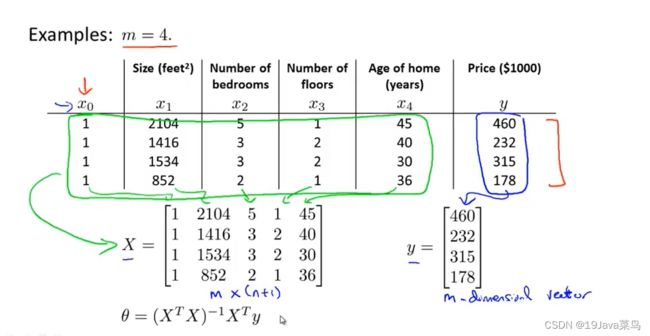
四,多变量线性回归
-4.1多变量线性回归假设函数
多变量及其假设函数
m:样本数量
n:每个样本的数据个数
x i x^{i} xi:第i个样本数据
x j i x^{i}_j xji:第i个样本数据中第j个数据
-4.2多元梯度下降法
-4.2.1特征缩放
均值归一化
x 1 x_1 x1= 元素值 − 均值 元素变化范围 \frac{元素值-均值}{元素变化范围} 元素变化范围元素值−均值
一般性写法
x i = x i − μ i σ x_i=\frac{x_i-μ_i}{σ} xi=σxi−μi
μ:平均值
σ:range(即max - min)
例1
x 1 x_1 x1= x 1 − 1000 2000 \frac{x_1-1000}{2000} 2000x1−1000
x 2 x_2 x2= x 2 − 2 5 \frac{x_2-2}{5} 5x2−2
1000和5是均值
-4.2.2学习率
学习率 α \alpha α选择方面
合适的 α \alpha α应该是:0.001,0.003,0.01,0.03,0.1,0.3,1,… …
每次都变化约为3的倍数逐步调试
-4.3特征和多项式回归
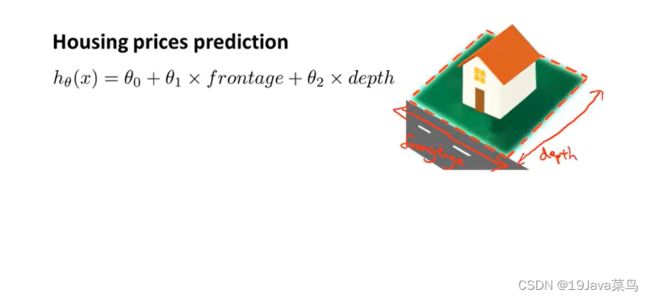
特征
特征:frontage,depth
模型函数 h θ ( x ) = θ 0 + θ 1 ⋅ f r o n t a g e + θ 2 ⋅ d e p t h h_θ(x) = θ_0 + θ_1·frontage+θ_2·depth hθ(x)=θ0+θ1⋅frontage+θ2⋅depth
由于房价与房子面积挂钩,所以有新特征
特征:size=frontage·depth
模型函数: h θ ( x ) = θ 0 + θ 1 ⋅ s i z e h_θ(x) = θ_0 + θ_1·size hθ(x)=θ0+θ1⋅size
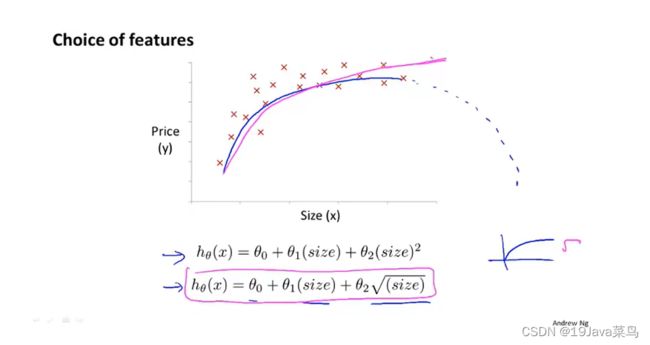
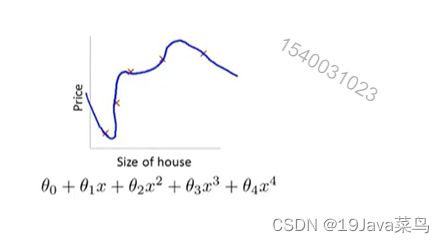
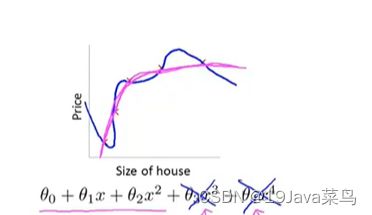
多项式回归
对于上述数据集
可以选择用二次函数 θ 0 + θ 1 ⋅ x + θ 2 ⋅ x 2 θ_0 + θ_1·x+θ_2·x^2 θ0+θ1⋅x+θ2⋅x2
二次函数或许不是好的选择,因为二次函数始终会降下来
现实中不会出现随着面积的增加房价反而下降的情况
也可以选择用三次函数 θ 0 + θ 1 ⋅ x + θ 2 ⋅ x 2 + θ 3 ⋅ x 3 θ_0 + θ_1·x+θ_2·x^2+θ_3·x^3 θ0+θ1⋅x+θ2⋅x2+θ3⋅x3
通过上述例子,只是想说明遇到函数拟合问题
可供选择的函数很多,而不是非要选择一条直线
-4.4正规方程
-4.4.1正规方程推导
正规方程与梯度下降比较
- 是同级算法
- 梯度下降缺点是需确定α,需要许多次迭代;优点是适用于样本量大(m > 10000)的数据
- 正规方程缺点是不适用于样本量大(m > 10000)的数据,但无需确定α,无需许多次迭代
4.正规方程法无需均值归一化
-4.4.2正规方程在矩阵不可逆情况解决方案
在Matlab或Octave中
pinv:求伪逆,无论矩阵是否有逆矩阵,均可求出解
inv:求逆,矩阵有逆矩阵有解
例1:pinv不可逆矩阵A的逆矩阵B,且A*B!=E
>> A=[1 2;3 4;5 6]
A =
1 2
3 4
5 6
>> inv(A)
错误使用 inv
矩阵必须为方阵。
>> pinv(A)
ans =
-1.3333 -0.3333 0.6667
1.0833 0.3333 -0.4167
>> B=pinv(A)
B =
-1.3333 -0.3333 0.6667
1.0833 0.3333 -0.4167
>> C=A*B
C =
0.8333 0.3333 -0.1667
0.3333 0.3333 0.3333
-0.1667 0.3333 0.8333
>>
例2:pinv不可逆矩阵A的逆矩阵B,且A*B=E
>> A=[1 2 3;4 5 6]
A =
1 2 3
4 5 6
>> inv(A)
错误使用 inv
矩阵必须为方阵。
>> pinv(A)
ans =
-0.9444 0.4444
-0.1111 0.1111
0.7222 -0.2222
>> B=pinv(A)
B =
-0.9444 0.4444
-0.1111 0.1111
0.7222 -0.2222
>> C=A*B
C =
1.0000 -0.0000
-0.0000 1.0000
>>
矩阵不可逆原因:
- 两个及两个以上的特征量呈线性关系,如 x 1 x_1 x1 = 3· x 2 x_2 x2
- 特征量过多。当样本量较小时,无法计算出那么多个偏导来求出结果
解决方案:
- 实际操作过程中,要删除多余特征,且呈线性关系的多个特征保留一个即可
- Octave中的pinv即使面对不可逆矩阵,也能计算出结果,得出来的是伪矩阵
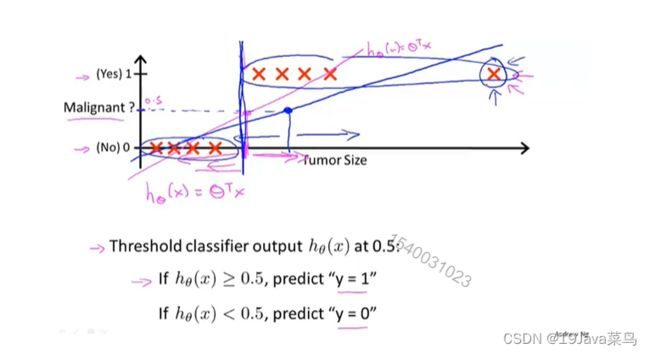
五,逻辑回归
-5.1分类问题
例2
如果我们在右侧多加一个数据,此时我们的假设函数将会变成蓝色
此时阈值为0.5,预估直线将从红色竖线变为蓝色属性
此时用直线拟合假设明显与实际不符
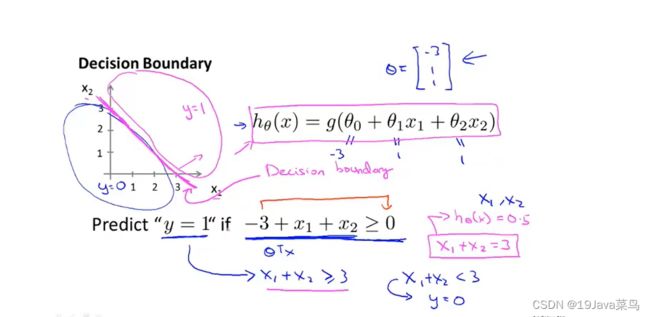
-5.2假设陈述
逻辑回归函数
h θ ( x ) = g ( θ T x ) h_θ(x) = g(θ^Tx) hθ(x)=g(θTx)
g ( z ) = 1 1 + e − z g(z)=\frac{1}{1+e^{-z}} g(z)=1+e−z1
合并求出
h θ ( x ) = 1 1 + e − θ T x h_θ(x) = \frac{1}{1+e^{-θ^Tx}} hθ(x)=1+e−θTx1
-5.3决策边界
-5.4代价函数
-5.4.1代价函数推导
Linner Regression
J ( θ 0 , θ 1 ) = 1 m ∑ i = 1 n ( 1 2 ⋅ h ( x ( i ) ) − y ( i ) ) 2 J(θ_0,θ_1)=\frac{1}{m}\sum_{i=1}^n(\frac{1}{2}·h(x^{(i)})-y^{(i)})^2 J(θ0,θ1)=m1∑i=1n(21⋅h(x(i))−y(i))2
令 1 2 ⋅ ( h θ ( x ( i ) ) − y ( i ) ) 2 \frac{1}{2}·(h_θ(x^{(i)})-y^{(i)})^2 21⋅(hθ(x(i))−y(i))2 = C o s t ( h θ ( x ) ( i ) , y ( i ) ) Cost(h_θ(x)^{(i)},y^{(i)}) Cost(hθ(x)(i),y(i))
则有 C o s t ( h θ ( x ) ( i ) , y ( i ) ) Cost(h_θ(x)^{(i)},y^{(i)}) Cost(hθ(x)(i),y(i))= 1 2 ⋅ ( h θ ( x ( i ) ) − y ( i ) ) 2 \frac{1}{2}·(h_θ(x^{(i)})-y^{(i)})^2 21⋅(hθ(x(i))−y(i))2
如果在逻辑回归中用线性回归的代价函数
由于 h θ h_θ hθ 实际为 g ( θ T ⋅ x ) g(θ^T·x) g(θT⋅x) ,会导致图像为非凸函数
很难得到全局最小代价函数
-5.4.2简化代价函数和梯度下降
注意:
- 逻辑回归的代价函数看似与线性回归的代价函数相同,但本质不同。
- 逻辑回归中的 h θ ( x ) = 1 1 + e − θ T ⋅ x h_θ(x) = \frac{1}{1+e^{-θ^T·x}} hθ(x)=1+e−θT⋅x1
- 线性回归中的 h θ ( x ) = θ T ⋅ x h_θ(x) = θ^T·x hθ(x)=θT⋅x
-5.5高级优化
利用一些高级算法和一些高级优化概念提高计算速度
- 能够自主选择α
- 速度大大快于梯度下降
- 比梯度下降更为复杂
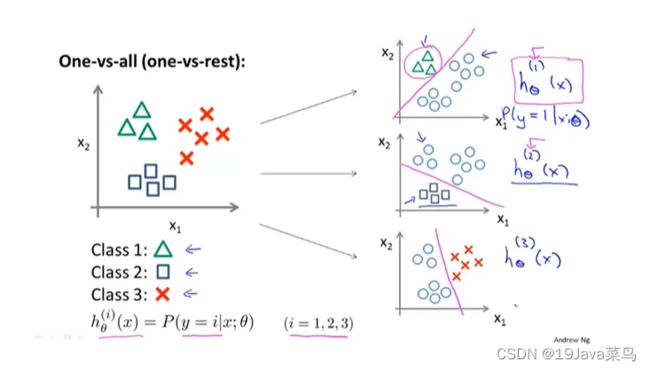
-5.6多元分类:一对多
六,正则化
-6.1 过拟合问题
过拟合: 当变量过多时,训练出来的假设能很好地拟合训练集,虽代价函数非常接近或等于0,但得到的曲线为了拟合数据集,导致它无法泛化到新的样本中,无法预测新样本数据
欠拟合: 无法很好的拟合训练数据集,这种算法具有高偏差
泛化: 指一个假设模型应用到新样本的能力
- 通过人工选择来舍弃一部分变量
- 模型选择算法
- 缺点:舍弃一部分特征变量也舍弃了关于问题的一些信息
- 正则化
- 减少特征量级或参数 θ j θ_j θj的大小
-6.2 过拟合代价函数
这个例子的代价函数
1 2 m ∑ i = 1 n ( h θ ( x ( i ) ) − y ( i ) ) 2 \frac{1}{2m}\sum_{i=1}^n(h_\theta(x^{(i)})-y^{(i)})^2 2m1∑i=1n(hθ(x(i))−y(i))2
代价函数加入惩罚项,让 θ 3 , θ 4 \theta_3,\theta_4 θ3,θ4特别小
1 2 m ∑ i = 1 n ( h θ ( x ( i ) ) − y ( i ) ) 2 + 1000 ⋅ θ 3 2 + 1000 ⋅ θ 4 2 \frac{1}{2m}\sum_{i=1}^n(h_\theta(x^{(i)})-y^{(i)})^2+1000·\theta_3^2+1000·\theta_4^2 2m1∑i=1n(hθ(x(i))−y(i))2+1000⋅θ32+1000⋅θ42
此时 θ 3 ≈ 0 , θ 4 ≈ = 0 \theta_3\approx0,\theta_4\approx=0 θ3≈0,θ4≈=0
此时的拟合数据图像
实际上我们无法预测那个 θ \theta θ 的次方项
所以正则化只需要把代价函数变为
J ( θ ) = 1 2 m [ ∑ i = 1 n ( h θ ( x ( i ) ) − y ( i ) ) 2 + λ ⋅ ∑ j = 1 n θ j 2 ] J(\theta)=\frac{1}{2m}[\sum_{i=1}^n(h_\theta(x^{(i)})-y^{(i)})^2+\lambda·\sum_{j=1}^n\theta_j^2] J(θ)=2m1[∑i=1n(hθ(x(i))−y(i))2+λ⋅∑j=1nθj2]
正则化项: λ ⋅ ∑ j = 1 n θ j 2 \lambda·\sum_{j=1}^n\theta_j^2 λ⋅∑j=1nθj2,作用是缩小每一个参数
正则化参数: λ \lambda λ,作用是控制两个不同目标之间的取舍
- 第一个目标与第一项有关,即我们想要更加拟合数据集
- 第二个目标与第二项有关,即我们想要参数θj尽量小
正则化代价函数
J ( θ ) = 1 2 m [ ∑ i = 1 n ( h θ ( x ( i ) ) − y ( i ) ) 2 + λ ⋅ ∑ j = 1 n θ j 2 ] J(\theta)=\frac{1}{2m}[\sum_{i=1}^n(h_\theta(x^{(i)})-y^{(i)})^2+\lambda·\sum_{j=1}^n\theta_j^2] J(θ)=2m1[∑i=1n(hθ(x(i))−y(i))2+λ⋅∑j=1nθj2]
优化目标
m i n J ( θ ) minJ(\theta) minJ(θ)
此时的拟合函数
-6.3 线性回归的正则化
梯度下降的正则化
Gradient descent
Repeat{
θ 0 : = θ 0 − α ⋅ 1 m ∑ i = 1 n ( h θ ( x ( i ) ) − y ( i ) ) ⋅ x 0 ( i ) θ_0:=θ_0-\alpha·\frac{1}{m}\sum_{i=1}^n(h_θ(x^{(i)})-y^{(i)})·x_0^{(i)} θ0:=θ0−α⋅m1∑i=1n(hθ(x(i))−y(i))⋅x0(i)
θ j : = θ j − α ⋅ [ 1 m ∑ i = 1 n ( h θ ( x ( i ) ) − y ( i ) ) ⋅ x j ( i ) + λ m ⋅ θ j ] θ_j:=θ_j-\alpha·[\frac{1}{m}\sum_{i=1}^n(h_θ(x^{(i)})-y^{(i)})·x_j^{(i)}+\frac{\lambda}{m}·\theta_j] θj:=θj−α⋅[m1∑i=1n(hθ(x(i))−y(i))⋅xj(i)+mλ⋅θj]
}
推出: θ j : = θ j ( 1 − α ⋅ λ m ) − α ⋅ 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) ⋅ x j ( i ) θ_j:=θ_j(1-\alpha·\frac{\lambda}{m})-\alpha·\frac{1}{m}\sum_{i=1}^m(h_θ(x^{(i)})-y^{(i)})·x_j^{(i)} θj:=θj(1−α⋅mλ)−α⋅m1∑i=1m(hθ(x(i))−y(i))⋅xj(i)
其中其中m是样本量,所以一般都是一个很大的值,λ 正则化参数,一般都不大。故 1 − α ⋅ λ m ≈ 0.99 1-\alpha·\frac{\lambda}{m}\approx0.99 1−α⋅mλ≈0.99,值比1略小
每次迭代时, θ j θ_j θj都乘这么一个比1略小的数,效果相当于梯度下降
-6.4 逻辑回归的正则化
七,神经网络
-7.1 非线性假设
无论是线性回归还是逻辑回归都有这样一个缺点,即:当特征太多时,
计算的负荷会非常大
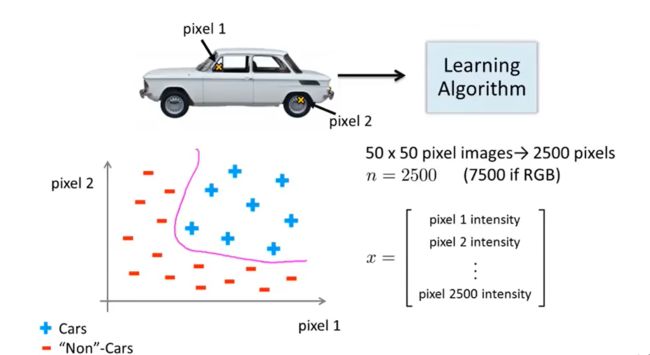
例2:鉴别是否是汽车
利用很多汽车的图片和很多非汽车的图片,然后利
用这些图片上一个个像素的值(饱和度或亮度)来作为特征。
例3:划分是否是汽车
给定数据集汽车和非汽车的数据,按照之前的方法划分
可以看到仅针对50*50像素的灰白图片,就有2500个特征值。当引入rgb时,特征值达到了7500个,如果算上多次多项式,特征值达到了三百万个,显然再继续用之前的算法难以处理这么庞大的数据
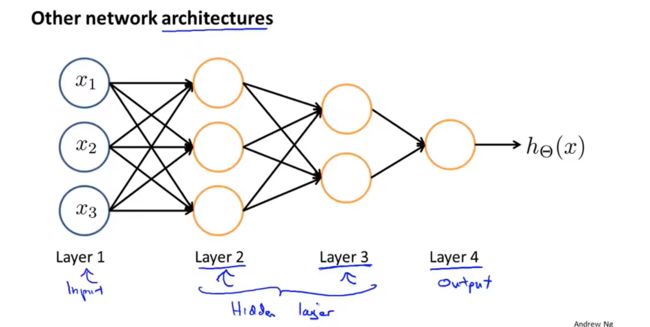
-7.2 神经元与大脑
-7.3 模型展示
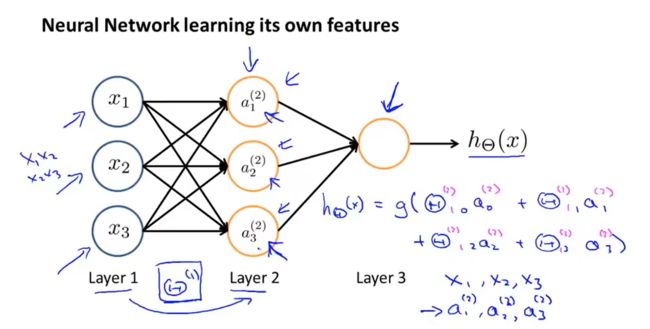
- x 0 , a 0 x_0,a_0 x0,a0为偏置单元,默认值为1
- a i ( j ) a_i^{(j)} ai(j)是第 j 层第 i 个神经元的激活值(即由一个具体神经元计算并输出的值)
- θ ( j ) θ^{(j)} θ(j)是权重矩阵,控制从第 j 层到第 j + 1层的映射
如果一个网络在第j层有 s j s_j sj个单元,在第j + 1层有 s j + 1 s_j +1 sj+1个单元,则矩阵 θ j θ_j θj的
维度为 s j + 1 ∗ ( s j + 1 ) s_j+1 * (s_j +1 ) sj+1∗(sj+1)。如 θ ( 2 ) θ^{(2)} θ(2)是3×4矩阵
向前传播: 从输入单元的激活项开始,进行前向传播给隐藏层,计算隐藏层的激活项,继续前向传播,并计算输出层的激活项
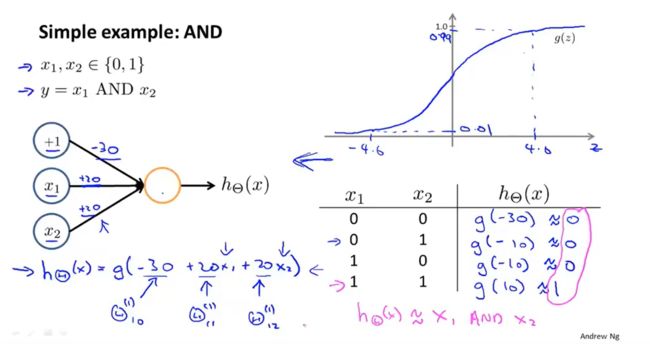
-7.4 例子与直觉理解
神经网络实现逻辑判断,解决上面左侧图的问题
- ( N O T x 1 ) A N D ( N O T x 2 ) (NOT x_1)AND(NOT x_2) (NOTx1)AND(NOTx2)
N O T 即结果取反。如果 x 1 输入为 1 ,则输出为 0 NOT即结果取反。如果x_1输入为1,则输出为0 NOT即结果取反。如果x1输入为1,则输出为0
x 1 输入 0 , h θ ( x 1 ) 输出 1 ; x 2 输入 0 , h θ ( x 2 ) 输出 1 ,再进行 A N D 运算可得最终结果 x_1输入0,h_θ(x_1)输出1;x2输入0,h_θ(x2)输出1,再进行AND运算可得最终结果 x1输入0,hθ(x1)输出1;x2输入0,hθ(x2)输出1,再进行AND运算可得最终结果
其他三种情况同理
- XNOR
有AND,(NOT x 1 x_1 x1)AND (NOT x 2 x_2 x2), OR三个前提
同样在输入层定义 x 0 , x 1 , x 2 x_0,x_1,x_2 x0,x1,x2
在隐藏层中
进行AND运算得到 a 1 ( 2 ) ,进行( N O T x 1 ) A N D ( N O T x 2 ) 运算得到 a 2 ( 2 ) a_1^{(2)},进行(NOT x_1)AND (NOT x_2)运算得到a_2^{(2)} a1(2),进行(NOTx1)AND(NOTx2)运算得到a2(2)
在输出层中
进行OR运算得到 a 1 ( 3 ) a_1^{(3)} a1(3),即为最终结果
每层都是通过计算不断复杂
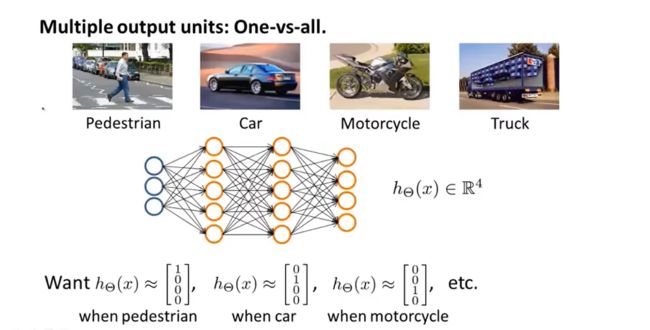
-7.5 多元分类
八,神经网络应用
-8.1 代价函数
这个看起来复杂很多的代价函数背后的思想还是一样的,我们希望通过代价函数来观察
算法预测的结果与真实情况的误差有多大,唯一不同的是,对于每一行特征,我们都会给出
k个预测,基本上我们可以利用循环,对每一行特征都预测k个不同结果,然后在利用循环
在k个预测中选择可能性最高的一个,将其与y中的实际数据进行比较。
正则化的那一项只是排除了每一层 θ 0 \theta_0 θ0后,每一层的 θ \theta θ 矩阵的和。最里层的循环j循环所
有的行(由 s l s_l sl +1 层的激活单元数决定),循环i则循环所有的列,由该层( s l s_l sl层)的激活单
元数所决定。即: h θ ( x ) h_\theta(x) hθ(x)与真实值之间的距离为每个样本每个类输出的加和,对参数进行regularization 的 bias 项处理所有参数的平方和
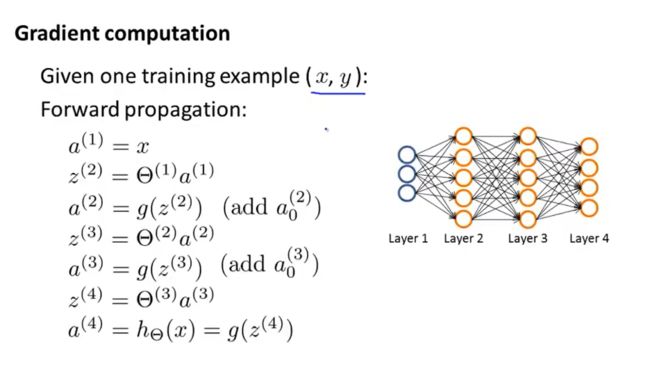
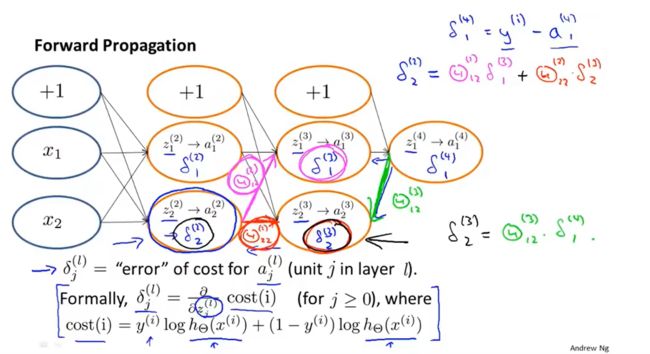
-8.2 反向传播算法
了计算代价函数的偏导数 ∂ ∂ θ i j ( l ) J ( θ ) \frac{\partial }{\partial θ_{ij}^{(l)}} J(θ) ∂θij(l)∂J(θ) ,我们需要采用一种反向传播算法,也就是
首先计算最后一层的误差,然后再一层一层反向求出各层的误差,直到
倒数第二层(第一层是输入变量,不存在误差)
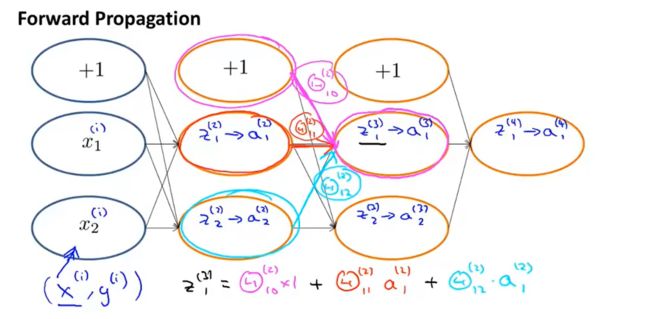
假设我们的训练集只有一个实例 ( x ( 1 ) , y ( 1 ) ) (x^{(1)},y^{(1)}) (x(1),y(1))我们的神经网络是一个四层的神经网络,
其中k = 4, S L S_L SL = 4,L= 4:
前向传播算法:
我们从最后一层的误差开始计算,误差是激活单元的预测 ( a k ( 4 ) ) (a_k^{(4)}) (ak(4))与实际值 ( y k ) (y^k) (yk)之间的误差,(k=1:k)
我们用 θ \theta θ来表示误差,则 θ ( 4 ) = α ( 4 ) − y \theta^{(4)}=\alpha^{(4)}-y θ(4)=α(4)−y
重要的是清楚地知道上面式子中上下标的含义:
代表目前所计算的是第几层。
代表目前计算层中的激活单元的下标,也将是下一层的第个输入变量的下标。
代表下一层中误差单元的下标,是受到权重矩阵中第行影响的下一层中的误差>单元的下标