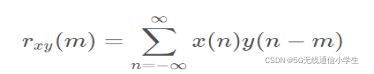NR ZC 序列相关与preamble检测原理

1.基本性质

在LTE系统中，PSS、SSS、cellRS、DMRS、SRS、PRACH、PUCCH信号基本上都涉及到了Zadoff –Chu信号，NR除了PSS和SSS信号采用M序列来生成抵抗大频偏场景，其它信号也同样涉及到了Zadoff–Chu序列。CAZAC(Constant Amplitude Zero Auto Correlation)，即为恒包络零自相关序列。

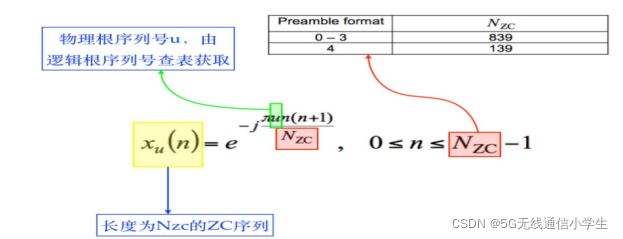
1）恒包络特性：任意长度的ZC序列幅值恒定，这也意味着功率恒定。从ZC序列的生成表达可以看到，本质就是一个底数为e的指数序列，每一个序列值代表单位圆上的一个点。每一个点值，仅是改变相位而已。复指数是一个二维I、Q的平面图。

其中u是物理根序列号（Physical root sequence number），由逻辑根序列号 

（Logical root sequence number)查协议表。

2）理想的周期自相关特性

 任意ZC序列移位n位后,n不是ZC序列的周期的整倍数(N不等于M*839/139)时,移位后的序列与原序列不相关。

3）良好的互相关特性：良好的互相关和部分相关值为0.

ZC序列循环移位N后，原序列只与移位后的序列得良好的相关峰值且峰值在N处，其它位置的相关峰值为0，这也是preamble检测的理论依据。

除此之外，两个根如果是互质的，生成的序列相关峰值几乎为零，也就是说不同的根序列生成的ZC序列不相关。我们知道一个根序列的长度是有限度的（139或者839），每移位NCS位就许配给一个UE，那由一个根生成的ZC序列很快用完，需要用到其它根来生成preamble，这个时候两个根生成的序列之间的互相关性就显得重要，它们要长得不“像”，即互相关几乎为0，否则基站区别不出它们。

4）低峰均比特性：任意ZC序列组成的信号，其峰值与其均值的比值很低。

5）傅里叶变换后仍然是ZC序列：任意ZC序列经过傅里叶正反变化后仍然是ZC序列。

6) 序列间的正交性
 (1) 相同root index的两个ZC序列彼此正交；
 (2) 不同root index的两个ZC序列由于其彼此互相关性非零，因此，不再具有正交性；

2.总结

同一个u(物理根序列号)生成的且经过不同的Cv移位的ZC序列，这些ZC序列分别不相关，既可以在时域上也可以再频域上求相关。

频域求相关是共轭对应点乘不累加，必须再转换到时域才能找到峰值。得到相关序列长度为N。

时域求相关是滑动点乘再累加，直接可以找到峰值 缺点是计算量大，得到相关序列长度为2N-1

时域求相关公式：

 

一般转成频域求相关：

1)两个复数信号的互相关函数的频域等于X信号频域的共轭乘以Y信号的频域，conj[fft(X)]*fft(Y)

 2）必须转到时域才可以找到Cv = V *Ncs 对应的峰值.

     比如u=1，且没有Cv移位(Cv=0)生成初始的ZC序列为ZC0，然后ZC1是ZC0循环移位1得到的，那么ZC0和ZC1做互相关运算，会在位移1的位置得到最大峰值，其他位置为0.   相关运算：corr = fft（ZC1）*conj[fft(ZC0)], ifft(corr).

如何两个物理根序列号互为质数（u1=1，u2 =3)且没有Cv移位(Cv=0)，分别生成初始ZC序列记为ZC0u1，ZC0u2，然后对初始序列ZC0进行不同的循环移位得到相应的ZC序列（ZC1u1,ZC2u1,…ZCmu1)和（ZC1u2,ZC2u2,…ZCmu2)，那么ZCmu1 与ZCmu2，（m=0,1,2,3……m）不相关,互相关为0即相关峰值为0.

Q1：为什么需要取共轭？

 A1: 自相关其实就是移动，相乘，求积分，看不同时刻的相似程度，显然不移动的相似程度是最高的，这里的自相关都是在实数上做的，在复数上，我们希望x(t)与x(t)本身或者移动后相乘再积分时，各时间点的值能够因叠加而增强。在实数域上x(t)直接自乘没有问题。在复数域上，x(t)自乘后角度是乱的，因此，如果对其中一个x(t)取一下共轭，相乘后辐角就统一变成0了，积分时就能够取得叠加增强的效果。

3. Matlab仿真

仿真参数配置如下：采用u =1，u = 838 生成两个根序列。

1）恒包络特性：任意长度的ZC序列幅值恒定，这也意味着功率恒定。

2）傅里叶变换后仍然是ZC序列

OFDM中功率归一化因子为 1/sqrt(N)，理论上要先除以一个 sqr(N)，然后再进行FFT，这里没有考虑这个因子，所以会产生一个sqrt(N)的幅度，即sqrt(839) = 28.965496.

3）良好的互相关特性 

ZC序列循环移位N后，原序列只与移位后的序列得良好的相关峰值且峰值在N处，其它位置的相关峰值为0. 这也是preamble 检测求相关的理论依据。

   前提条件： u = 1， seq1为base seq，seq2 为移位 v=26的序列，X1((n+26)mod839)。corr(seq1,seq2)

  (1）可以看出在index = 27(理论上index 26位置，因为matlab index不能从0开始，只能从1开始)的位置出现峰值。

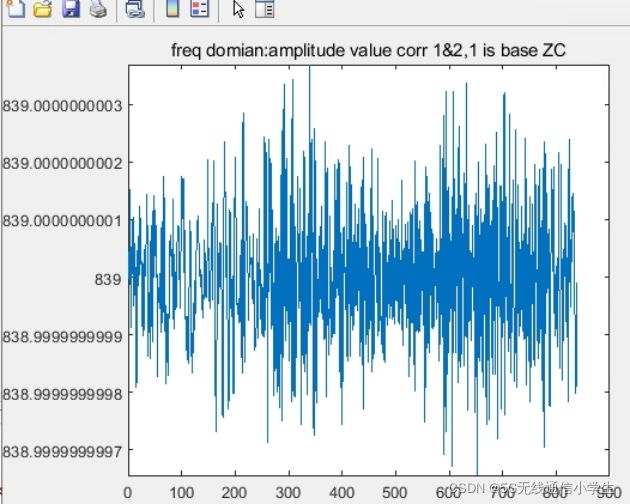
  (2) 求相关后在频域上得到的幅值基本上恒定，不能区分，必须转到时域上才能得到峰值。

 

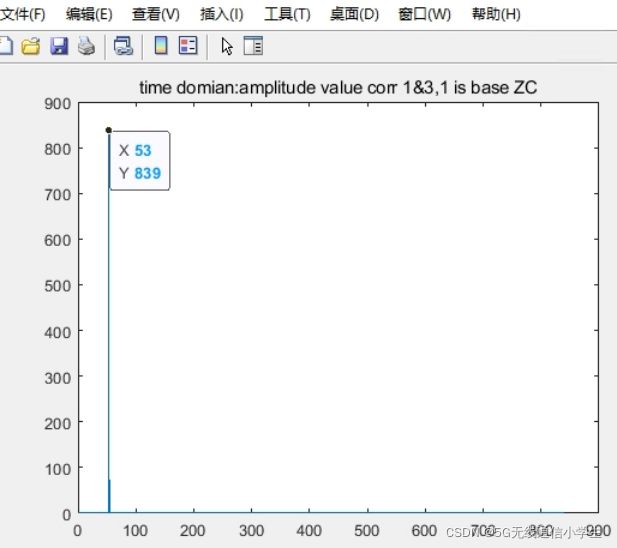
前提条件： u = 1， seq1为base seq，seq3为移位 v=2*26的序列，X1((n+2*26)mod839)。 corr(seq1,seq3)

  (1）可以看出在index = 53(理论上index 52位置，因为matlab index不能从0开始，只能从1开始)的位置出现峰值。

  (2) 求相关后在频域上得到的幅值基本上恒定，不能区分，必须转到时域上才能得到峰值。

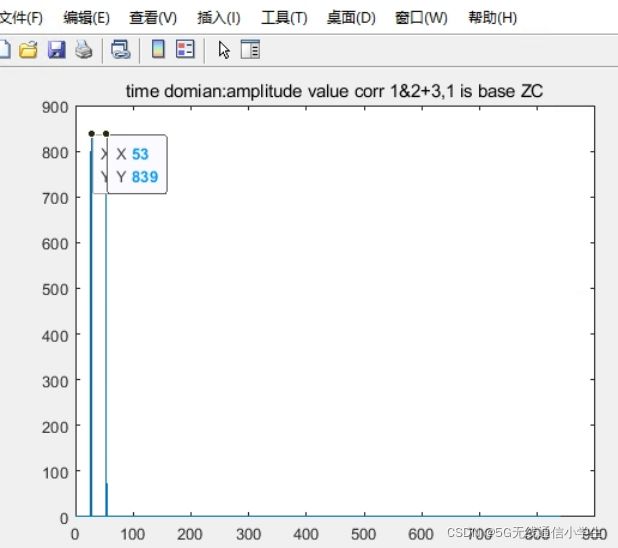
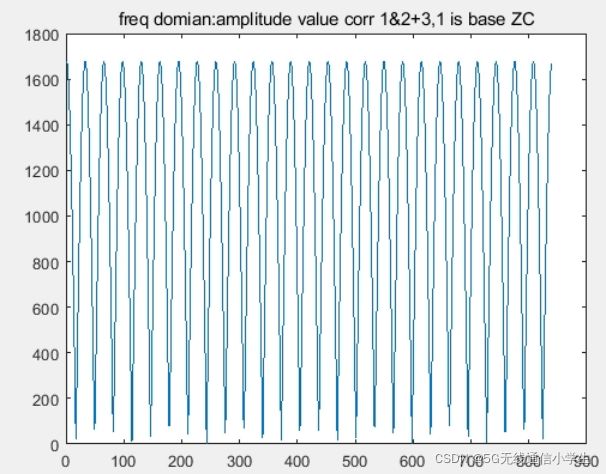
 前提条件： u = 1， seq1为base seq，seq2 为移位 v=26的序列，X1((n+26)mod839), seq3为移位 v=2*26的序列，X1((n+2*26)mod839)。corr(seq1,seq2+seq3)

  (1) 可以看出在index = 26, 53 (理论上index 26,53位置，因为matlab index不能从0开始，只能从1开始)的位置出现峰值。

  (2) 求相关后在频域上得到的幅值基本上恒定，不能区分，必须转到时域上才能得到峰值。

  (3) 同一个根序列产生的多个seq叠加在一起，仍然可以挑选出来。

前提条件：u = 1, seq2 为移位 v=26的序列，X1((n+26)mod839)

             u = 838, seq2 为移位 v=26的序列，X838((n+26)mod839)    corr(seq2,seq2)

  (1) 不同的根序列产生的seq互不相关。

  (2) 求相关后在时域和频域上得到的幅值基本上恒定，不能区分。

4）也可以直接时域求相关得到峰值点：

   前提条件： u = 1， seq1为base seq，seq2 为移位 v=26的序列，X1((n+26)mod839)。corr(seq1,seq2)，corr(seq1,seq2+seq3)

  (1）可以看出在index = 27（865-838）(理论上index 26位置，因为matlab index不能从0开始，只能从1开始)的位置出现峰值。

  (2）可以看出在index = 27,53（865-838,891-838）的位置出现峰值。

3.1 仿真总结

1）preamble检测根据ZC序列的性质，既可以从频域求相关，也可以从时域求相关。

2）频域求相关是共轭点乘不累加，必须再转换到时域才能找到峰值。

3）时域求相关是滑动点乘再累加，直接可以找到峰值，缺点是计算量大。

4. 参考

数字信号处理中的自相关和互相关计算和物理意义

自相关的物理意义

NR-PRACH接受端如何检测出preambleid和TA的

PRACH的生成 （5G的NR）

LTE-TDD随机接入过程（5）-怎么生成64个前导码序列