【强化学习】决策优化问题与Gymnasium环境
强化学习-1
老虎机与优化策略
老虎机大家应该都玩过
看到连成一条线的时候再摁下去,它其实是连不上的,要赢得游戏需要一些策略。
寻找最优策略和强化学习
如何找到最优策略,这种最优策略其实本来是运筹学 (operation research)中的概念,属于优化问题。
经典的优化问题有
- 背包问题
- 最短路径
- … …
虽然这些问题也是在寻找最优策略,但是和强化学习的寻找方法其实不一样。
上面老虎机的场景,是一个典型的强化学习的问题——一个典型的决策性的问题。我们想要让某个东西连成一条线,想让收入最大化,如果我们的每一步都让收益最大化。那么最终的结果可能反而会变差。
它在这里做了一个统计,\epsilion等于零,它指的是看到这个老虎机恰好要连上的时候摁下按钮。\epsilion等于0.1、0.01,就是有个差值。就比方说0.01就是有99%的概率,它是在线快到的时候摁下去;有1%的概率,它不是在那个线快到的时候摁下去。那么0.1的话就是有90%的概率是线快到的时候摁下去;有10%是不是在那个线快到的时候摁下去。
结果证明——一定的随机可以大幅地提高平均收益。
老虎机的研究是一个例子,它说明我们在做这个决定的时候,假设想要让它的目标是G,但是如果每次冲着它是G的话,达到结果并不能如你所愿。
围棋与长线决策
在AlphaGo出世之后,围棋与强化学习似乎也进行了深绑定。
围棋
【规则】因为简单所以困难
目标:围棋的目标是占领比对手更多的领地,也可以通过围围对手的棋子来获得得分。玩家通常会使用黑子和白子来代表自己和对手。
棋盘:围棋使用一个19x19的网格状棋盘,但也有9x9和13x13的小棋盘变种。网格上的交叉点被称为“点”。
初始布局:游戏开始时,棋盘上没有棋子。玩家轮流在交叉点上放置自己的棋子,一方为黑子,另一方为白子。
自由交叉点:玩家可以在棋盘上的自由交叉点上放置棋子。交叉点必须是空的,不能重叠,且不能直接导致自己的棋子被围。
围棋:当一个或多个棋子被对方的棋子完全围住,它们被认为是被吃掉的,并从棋盘上移除。围住对方的棋子可以获得得分。
连通性:相邻的相同颜色的棋子在垂直和水平方向上是连通的,它们一起形成一个“群”。如果一个群被完全围住,那么整个群都会被吃掉。
禁止的着法:在某些情况下,由于规则(劫)限制,玩家不能重复上一回合的棋局。
结束游戏:游戏结束当双方都同意不再放置更多的棋子,或者当棋盘上没有更多的空交叉点。然后,通过计算每个玩家占领的领地和所吃掉对方的棋子来确定最终得分。
复杂之处
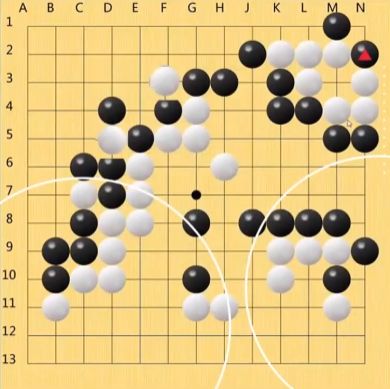
当旗手现在获得了更大的面积,但下一步可能面积获得更小了,甚至旗手将丢掉更大的面积。
这个时候,虽然说已给定目标,即要获得尽可能更多的面积,但是我们在这一步去做的时候会发现,从长远来看反而是损失了。那也正是它复杂之处。
现在这个是13乘13的,它还相对来说较简单。围棋的话,它正规棋盘是19乘19,它是361个点。那么换句话说,我们现在要去找该走哪个位置的时候,首先这里有361种可能,我们走完之后我还得去考虑黑棋有怎么走法。那么黑棋在这个时候就有360种走法,还有可能我吃掉子之后,我们别的地方又可以走了…
结果其实是一个接近于361次方的东西。
假如说我们现在每一走一步要往前看七步,这将会是一个极大的数字,那么如果我们要下的很多,这可能得二三十步。这个数字会是一个极大的数字就是计算机根本就运行不起来的计算量。
因此以围棋为代表的这种长线决策问题,计算机就很难做了。
累计收益最大化
举了两个例子,那么为什么强化学习相关的优化问题与其他优化问题到底有哪里不同?
在强化学习相关的优化问题中,我们常需要找到最优解而避免被短期的最优解所影响——这有点类似局部最优解不是全局最优解的概念,但是又有区别。
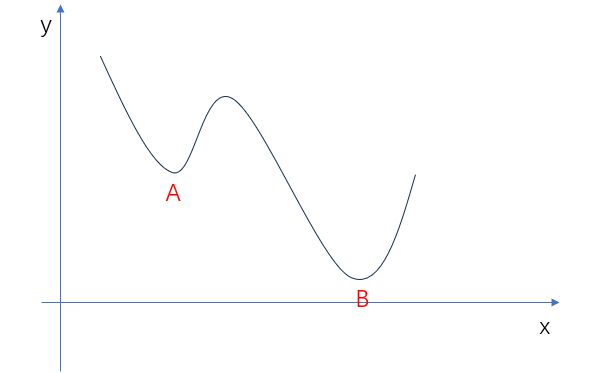
区别在于,假如说我们要找最小值,那么这个A点是它的局部最优,这个B点是它的全局最优,但是这个时候的条件是——这个函数其实它已经它其实已经既定了
但是要注意,强化学习要解决的问题中的横轴不是X,而是时间
G = m a x i m u m ( ∑ t ∈ T R t ) G = maximum(\sum_{t\in T}R_t) G=maximum(t∈T∑Rt)
如果在每一步的话,我们都想去最大化,最终的G其实可能会变得更糟。
所以这里问题的本质其实是要使累积的收益最大化
困难点:
-
未来的条件不能预测
-
每一步决策都会影响后续决策
如果选择不对,可能会越走越偏
现实生活中,人们解决长线决策问题往往是通过”代偿“的方式,比如——组合收益和对冲基金。
形象的来说,计算机视觉和NLP其实是让计算机长眼睛 (或者说让我们的模型长眼睛),而强化学习则是要让计算机长脑子——不能只看我们当前的情况,得仔细的去盘算一下,看整个长线的决策应该怎么做。
强化学习的应用场景
- 自动驾驶
- 金融量化 投资收益
- 游戏
所有智力行为几乎都可以归类为强化学习问题。
我们如何解决这类问题?
在s_t状态下选择a_t的概率 × 在s_t状态下选择a_t的条件下r_t的概率 × reward值
在所有的时间轴T上,所有的动作状态,所有的reward状态
目标是将这个东西最大化
\theta是参数
在给定a|s_t的情况下,如何调整参数\theta,使得最后得到的值最大。
f ( a ∣ s t ; θ ) , s . t a r g m a x θ [ ∑ t → T ∑ a t ∈ A ∑ r t ∈ R P r ( a t ∣ s t ) P r ( r t ∣ ( s t , a t ) ) ∗ R t ] f(a | s_t; \theta), s.t\space argmax_{\theta}\left[\sum_{t\rightarrow T} \sum_{a_t \in \mathbf{A}}\sum_{r_t\in \mathbf{R}}Pr(a_t | s_t) Pr(r_t|(s_t, a_t)) * R_t\right] f(a∣st;θ),s.t argmaxθ[t→T∑at∈A∑rt∈R∑Pr(at∣st)Pr(rt∣(st,at))∗Rt]
Terminologies 术语
-
agent:存在于某个环境 (environment)中,接受反馈,反馈会以reward的形式,在每个时间步骤反馈给agent。 -
a:action,即要让agent来进行的动作,用
A \mathcal{A} A
表示所有action的集合。 -
r_t:reward,环境给agent每个步骤可以量化的一个反馈。 -
G_t:goal,指在t时刻,agent在未来所有的reward的总和比如,第1天上班,
G_t指的就是未来t天的收入总和;第2天上班,G_t指的就是未来t-1天的收入总和——因为过去的东西 (第一天的收入) 已经不能优化了用
G = ∑ t ∈ T r t \mathcal{G} = \sum_{t \in T} r_t G=t∈T∑rt
表示未来这段时间的goal。 -
environment:环境,一种反馈规则,agent不能改变或者不能按照其目的改变。比较好的一种理解就是——环境是一种客观条件,不随agent的改变而改变
比如,公司找了一批实习生,根据绩效给每个人发工资,“根据绩效发工资”这个反馈规则就是一种环境。但是实习生中有一个是领导的儿子,即使他绩效不达标也得给他发满工资,那么这时“根据绩效发工资”这个反馈规则就不能视作一种环境。
-
s_t:state,环境中agent能观察到的信息,用
S \mathcal{S} S
表示所有state的集合。 -
f,或者时常被看到叫做\pi:policy-
case1:
π ( s t ) − > a \pi(s_t) -> a π(st)−>a
最后生成一个动作; -
case2:
π ( a , s t ) ∈ [ 0 , 1 ] \pi(a, s_t) \in [0, 1] π(a,st)∈[0,1]
输入a和s_t,目的是要评价这个在当前状态下获得这个action的概率。
两者之间的关系可以用下式来表达
π ( s t ) = a r g m a x a ∈ ∣ A ∣ π ( a , s t ) \pi(s_t) = argmax_{a\in|A|}\pi(a, s_t) π(st)=argmaxa∈∣A∣π(a,st) -
-
return:基于
π p ( s t ) \pi_p(s_t) πp(st)
这个policy § 和具体到某时某刻 (t) 的state,未来rewards的总和。比如,在公司一天收入200¥,按周结算,那么第二天的
G就是800¥ (是理论上可以获得的);但是如果改变policy为今天去跟那个领导儿子打一架,那这个reward明天就变了,return就是指基于现在的这个s_t状态和策略下我们的reward的总和是多少 (很可能是0¥)。 -
value:一种评价,value(s_t) = 此时此刻t的return- 在不同的state下,value由reward得到:
比如,下围棋的例子,模型能够下棋需要知道在不同的state情况下是好是坏,那么此时就需要有一个value来判别此时情况的好坏,而好坏也是根据我们那个reward给过来的
这里就可以理解为——不同的棋局 (state) 下,总的收入应该是多少。
- 在相同的state下,value受policy的影响:
再比方说,老张老刘老王三个人,他们每个人都有各自的一个打牌的策略,当他们看见同样一副牌 (state是一样的),但他们对这副牌的评价——由于policy不一样——于是最终给定的这个value就不一样了。
-
quality:质量,本来是运筹学里边的一个概念q(a, s) —— 表示此时此刻t下,执行了动作a后期望的value是多少
q ( a t , s t ) ∈ R v a l u e ( s t ) = E x p P r ( a t ∣ s t ) ∗ q ( a t , s t ) q(a_t, s_t) \in \mathbf{R}\\ value(s_t) = \mathbb{Exp}Pr(a_t|s_t)*q(a_t,s_t) q(at,st)∈Rvalue(st)=ExpPr(at∣st)∗q(at,st)
有人可能会问这里为什么要求一个期望?因为在某个状态下,一个人要获得什么动作,其实是一个概率问题,而非一个固定值 (某个state下,agent做某个action其实是概率问题)。
比方说打牌的时候,小李第一个出牌,出了个“三三四四五五”,最后赢了。当下一轮时,小李又拿到了“三三四四五五”,但这一轮是否先出这个并不一定,小李下一副出什么牌是一种概率(如果不是概率那就市区决策的意义了)。
还有几个重要概念就一并说掉了
-
optimal 最优的 policy
π ∗ ( s t ) \pi_*(s_t) π∗(st) -
optimal 最优的 policy 下它的 q 值
q ∗ ( a t , s t ) q_*(a_t, s_t) q∗(at,st) -
optimal 最优的 policy 下它的 v 值
v ∗ ( a t , s t ) v_*(a_t, s_t) v∗(at,st)
一种上古时期的解决办法
强化学习解决优化问题的方法,有点类似心理学和生物学中巴普洛夫和狗的实验,让模型不断地去尝试,最终总结出一些经验教训,这就是强化学习。
蒙特卡洛模拟 Monte Carlo
For the probability computing in gambling
任何赌场里边新手入门第一堂课,叫做21点,也叫做Black Jack。
Blackjack
The object of the popular casino card game of blackjack is toobtain cards the sum of whose numerical values is as great as possible without exceeding 21. All face cards count as 10, and an ace can count either as 1 or as 11. We considerthe version in which each player competes independently against the dealer. The gamebegins with two cards dealt to both dealer and player. One of the dealer’s cards is faceup and the other is face down. If the player has 21 immediately (an ace and a 10-card).it is called a natural. He then wins unless the dealer also has a natural, in which case thegame is a draw. If the player does not have a natural, then he can request additionalcards, one by one (hits), until he either stops (sticks) or exceeds 21 (goes bust). If he goesbust, he loses; if he sticks, then it becomes the dealer’s turn. The dealer hits or sticks according to a fixed strategy without choice: he sticks on any sum of 17 or greater, andhits otherwise. If the dealer goes bust, then the player wins; otherwise, the outcome -win, lose, or drawis determnined by whose final sum is closer to 21.
Gym
在介绍完21点规则之后,使用强化学习解决21点问题之前,我们有必要介绍一下强化学习的环境——Gymnasium。
Black Jack
This environment is part of the Toy Text environments which contains general information about the environment.
| Action Space | Discrete(2) |
| Observation Space | Tuple(Discrete(32), Discrete(11), Discrete(2)) |
| import | gymnasium.make("Blackjack-v1") |
-
Action Space指的是动作空间有0和10:hits1:sticks
-
Observation Space观察空间是(32, 11, 2),因为player手牌值有0~31,dealer亮出手牌值有1~11,Aces有0或1两种个状态 -
Starting State
The starting state is initialised in the following range.
| Observation | Min | Max |
|---|---|---|
| Player current sum | 4 | 12 |
| Dealer showing card value | 2 | 11 |
| Usable Ace | 0 | 1 |
-
Rewards-
win game: +1
-
lose game: -1
-
draw game: 0
-
win game with natural blackjack: +1.5 (if natural is True) +1 (if natural is False)
observation, reward, terminated, truncated, info = env.step(action)
-
Black Jack 胜率提高
import gymnasium as gym
env = gym.make('Blackjack-v1', natural=False, sab=False, render_mode='rgb_array')
env.action_space.sample()
### Output:
### 0 or 1
state, info = env.reset()
state
### Output:
### (10, 6, 0)
我们现在希望让程序解决这个问题,给定一个state,能够产出player现在该 hit 还是 stick。此外我们还要获得一个policy函数,能够使得每一步的rewards加起来尽可能大。
Step1: Value Estimation: Evaluation
Target: We want to know different states and their value, which is accumulated by rewards
episode = 1000000
trajectories = [[]]
for _ in range(episode):
state, info = env.reset()
while True:
action = env.action_space.sample()
state_next, reward, terminated, truncated, info = env.step(action)
# (s, a, r)
trajectories[-1].append( (state, action, reward) )
state = state_next
if terminated or truncated:
trajectories.append( [] )
break
env.close()
trajectories[3]
### Output:
### [((17, 3, 0), 0, 0.0)]
如何计算Value
v a l u e ( s 0 ) = r 0 + r 1 + r 2 + ⋯ + r T v a l u e ( s 0 ) = r 0 + v a l u e ( s 1 ) value(s_0) = r_0+r_1+r_2+\cdots+r_T\\ value(s_0) = r_0+value(s_1) value(s0)=r0+r1+r2+⋯+rTvalue(s0)=r0+value(s1)
Value是估计值,为了估计的准确,需要乘上一个参数\gamma
假如发工资的情景,上个月的工资是按周发的,每天200¥,上月工资已到手;
这个月老板说,换个激励方式:一周中每天的工资逐步递增(50¥ 150¥ 300¥ 400¥ 500¥),总额大于1000¥,但后一天的工资是否能拿到取决于前一天的任务是否完成。
问:你更愿意按照上个月的方式,还是老板新给出的方式?
如果选择新的方式,其实是承担了一定风险,这些风险所带来的损失也应该被纳入我们的决策 (比较) 过程中去。比如给收益value(s_1)乘上0.8,说明后些天到手的1350¥只能相当于没有风险的1080¥(简单地说就是对未来有个折扣)。
v a l u e ( s 0 ) = r 0 + γ ∗ v a l u e ( s 1 ) , γ ∈ ( 0 , 1 ) value(s_0) = r_0 + \gamma*value(s_1), \gamma \in(0, 1) value(s0)=r0+γ∗value(s1),γ∈(0,1)
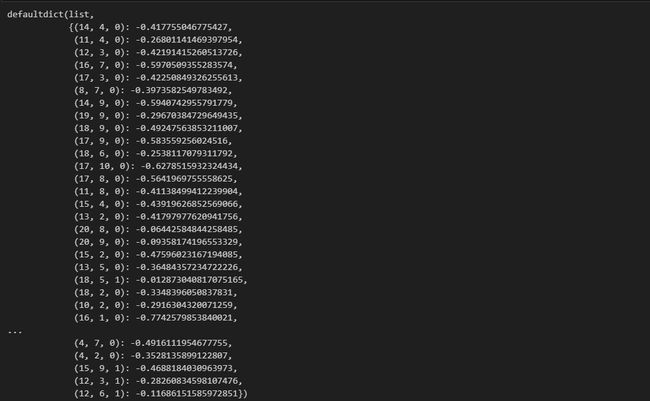
实际采样过程中获得的rewards之和,记为Goal(Goal就是根据现在的rewards得到的一个值,value则是根据Goal来进行估计的)
from collections import defaultdict
import numpy as np
gamma = 0.99
G = 0
values = defaultdict(list)
for i, t in enumerate(trajectories):
G = 0
for (s, a, r) in t[::-1]:
G = r + gamma * G
values[s].append(G)
for s, Gs in values.items():
values[s] = np.mean(Gs)
values
Step2: Controlling
Based on states’ evaluations, getting the prospected action a_i
import numpy as np
value_with_ace = np.zeros((20 + 10, 11))
value_without_ace = np.zeros((20 + 10, 11))
# 使用列表生成式将所有元素设置为np.nan
value_with_ace[:] = np.nan
value_without_ace[:] = np.nan
# 降维
for (p, d, a), v in values.items():
if a:
value_with_ace[p][d] = v
else:
value_without_ace[p][d] = v
我们可以对胜率情况进行可视化
import matplotlib.pyplot as plts_value = plt.imshow(value_with_ace) plt.colorbar(s_value)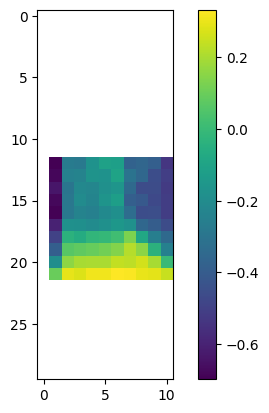
还可以进行3D可视化
from mpl_toolkits.mplot3d import Axes3D%matplotlib widgetfig = plt.figure() ax = fig.add_subplot(111, projection='3d') X, Y = np.meshgrid(np.arange(value_with_ace.shape[0]), np.arange(value_without_ace.shape[1])) def get_z(x, y, ace): data_source = value_with_ace if ace else value_without_ace return value_without_ace[x][y] Z = np.array([get_z(x,y,ace=False) for x,y in zip(np.ravel(X), np.ravel(Y))]).reshape(X.shape) ax.scatter(X, Y, Z) ax.set_xlabel('Player Current Sum') ax.set_ylabel("Dealer Show") ax.set_zlabel("State Value") plt.show()
此时的policy:让我们的action能够找到更大的value即可.
gamma = 0.99
values_with_action = defaultdict(list)
Q_table = defaultdict(lambda : [0, 0]) # 默认长度为2的list ———— action-0, state: value action-1, state: value
# values = defaultdict(list)
for i, t in enumerate(trajectories):
G = 0
for (s, a, r) in t[::-1]:
G = r + gamma * G
values_with_action[(s, a)].append(G)
for (s, a), Gs in values_with_action.items():
Q_table[s][a] = np.mean(Gs)
Q_table[(18, 4, 0)]
### Output:
### [0.17818999437886454, -0.7948415121255349]
def policy(state):
global Q_table
return np.argmax(Q_table[state])
episode = 1000000
trajectories = [[]]
win_or_loss = []
for _ in range(episode):
state, info = env.reset()
while True:
action = policy(state)
state_next, reward, terminated, truncated, info = env.step(action)
# (s, a, r)
trajectories[-1].append( (state, action, reward) )
state = state_next
if terminated or truncated:
trajectories.append( [] )
if reward == 1: win_or_loss.append(1)
else : win_or_loss.append(0)
break
env.close()
sum(win_or_loss) / len(win_or_loss)
### Output:
### 0.38037
对比一下随机policy
episode = 1000000
trajectories = [[]]
win_or_loss = []
for _ in range(episode):
state, info = env.reset()
while True:
action = env.action_space.sample()
state_next, reward, terminated, truncated, info = env.step(action)
# (s, a, r)
trajectories[-1].append( (state, action, reward) )
state = state_next
if terminated or truncated:
trajectories.append( [] )
if reward == 1: win_or_loss.append(1)
else : win_or_loss.append(0)
break
env.close()
sum(win_or_loss) / len(win_or_loss)
### Output:
### 0.27994
胜率提升了超过10个百分点。
1. 上文中的过程,先收集很多sampling,再统一更新(off-line training); (on-linetraining)一边收集 一遍更新policy.
todo: 将代码改变成 online training的方式,并且思考,这两种训练方式,有何优劣? 有何异同?
Online Variation
import gymnasium as gym
from collections import defaultdict
import numpy as np
import random
env = gym.make('Blackjack-v1', natural=False, sab=False, render_mode='rgb_array')
gamma = 0.99
Q_table = defaultdict(lambda : [0, 0])
def policy(state):
global Q_table
if state not in Q_table: # 如果状态不在 Q 表格中,初始化 Q 值
Q_table[state] = [0, 0]
return env.action_space.sample()
else: # 选择最优动作
return np.argmax(Q_table[state])
episode = 100000
trajectories = [[]]
win_or_loss = []
for _ in range(episode):
state, info = env.reset()
while True:
action = policy(state)
state_next, reward, terminated, truncated, info = env.step(action)
# (s, a, r)
trajectories[-1].append( (state, action, reward) )
state = state_next
if terminated or truncated:
trajectories.append( [] )
if reward == 1: win_or_loss.append(1)
else : win_or_loss.append(0)
break
env.close()
sum(win_or_loss) / len(win_or_loss)
### Output:
### 0.38114
优劣 & 异同
Offline Training
- 对数据利用更充分
- 貌似结果更加稳定
Online Training
- 能够快速响应环境变化,因为它能够及时更新策略或价值函数
2. 目前的”胜率”是40%,你能否想办法改变一些代码,将这个胜率提升到44%?
import gymnasium as gym
# 创建 BlackJack 游戏环境
env = gym.make('Blackjack-v1', natural=False, sab=False, render_mode='rgb_array')
gamma = 0.01
learning_rate = 0.2
Q_table = defaultdict(lambda : [0, 0])
def epsilon_greedy_policy(state, epsilon):
global Q_table
if state not in Q_table: # 如果状态不在 Q 表格中,初始化 Q 值
Q_table[state] = [0, 0]
if random.random() < epsilon: # 以 epsilon 的概率随机选择动作
return env.action_space.sample()
else: # 以 1 - epsilon 的概率选择最优动作
return np.argmax(Q_table[state])
episode = 100000
win_or_loss = []
for _ in range(episode):
state, info = env.reset()
epsilon = 1.0 / ((_) + 1) # 随着时间逐渐降低 epsilon,实现探索-利用平衡
while True:
action = epsilon_greedy_policy(state, epsilon)
state_next, reward, terminated, truncated, info = env.step(action)
if state not in Q_table:
Q_table[state] = [0, 0]
# 更新 Q 值
Q_table[state][action] += learning_rate * (reward + gamma * max(Q_table[state_next]) - Q_table[state][action])
state = state_next
if terminated or truncated:
if reward == 1: win_or_loss.append(1)
else : win_or_loss.append(0)
break
env.close()
sum(win_or_loss) / len(win_or_loss)
### Output:
### 0.41261
只能提高到41%,不过似乎gamma越小胜率越高?
3. 强化学习和监督学习(Supervised Learning)和非监督学习(unsupervised learning)最大的区别是什么?强化学习和Optimization的关系是什么?
主要区别:
- 监督学习需要明确的输入-输出对,而非监督学习和强化学习通常没有明确的输出标签。
- 监督学习和非监督学习中每个数据点都是独立的,而强化学习是状态相关的,决策会影响未来的状态和奖励。
- 强化学习涉及agent在与environment互动的过程中学习,监督学习和非监督学习不需要与environment进行交互
- 监督学习常用于回归问题,非监督学习常用于聚类问题,强化学习常用于决策问题。
强化学习与Optimization的关系:
一切在某种约束情况下找到最优解的过程,都可以叫做优化。
我理解强化学习和优化的区别:
强化学习
- 是一种学习方式
- 其目标是通过与环境的互动来学习制定策略,以最大化长期回报其目标问题是控制问题和决策问题
优化
- 是一种数学问题解决方法
- 其目标是找到参数的最佳组合以最大化或最小化一个特定的目标函数
- 它的目标问题是参数优化问题,如参数调整和函数拟合