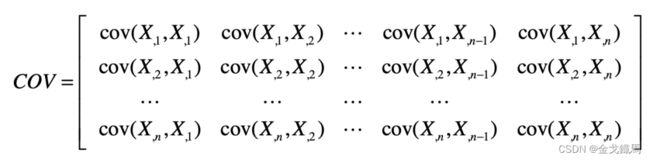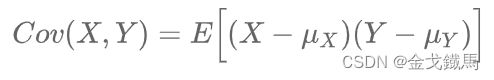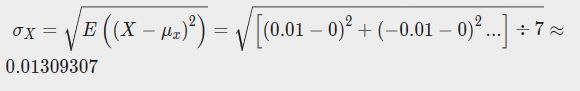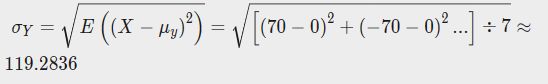详解“协方差”与“相关系数”

引言

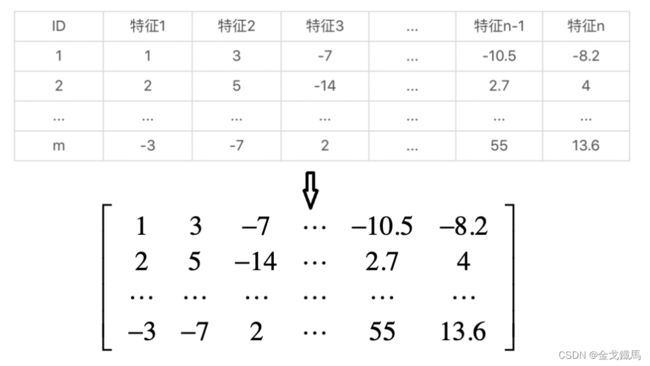
        PCA的目标对象是矩阵，例如，有m个样本，每个样本有n个特征，那么就可以构造成一个样本矩阵，并转换成矩阵的形式。

        PCA的最终目的是减少特征的个数，去掉那些不重要的特征，也就是减小矩阵列向量的个数，为后续分类任务实现数据预处理的作用。

        那如何识别出矩阵中有用的列？PCA的做法是应用矩阵的特征值分解。特征值分解要求矩阵是方阵，但实际上样本的数量m要远大于特征的数量n，既然不满足特征值分解的条件，那就要想办法创造条件，其中一种方法是通过m*n原始矩阵构造出n*n的协方差矩阵。

 协方差矩阵：   

 

        虽然实现了最终的目的，但针对协方差矩阵的每个元素的真正含义并没有过多的解释，这就导致很多人不明白，为什么对协方差矩阵进行特征值分解就能进行降维？下面就逐一进行讲解。

协方差：

        也即是上面协方差矩阵中每一个元素：，协方差就是用来衡量变量X和变量Y相关性的指标，通俗的讲：

（1）如果X变大，Y也变大，那么就说X和Y同向变化，X和Y正相关，此时的协方差为正数。

（）如果X变大，Y变小，那么就说X和Y反向变化，X和Y负相关，此时的协方差为负数。

数值越大，说明相关性越大。

协方差的计算公式：

公式的解释：

    如果有X, Y两个变量，每个时刻的“X值与其均值之差”乘以“Y值与其均值之差”得到一个乘积，再对这每个时刻的乘积求和并求出均值。

    特别的有 ，也就是说：方差是一种特殊的协方差。

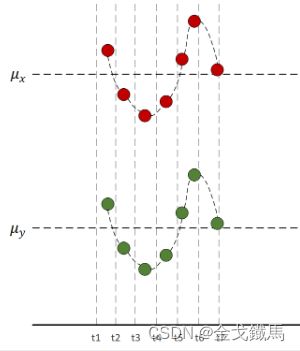
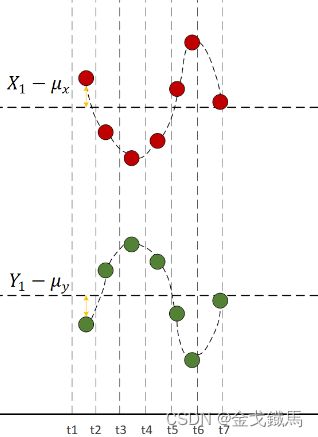
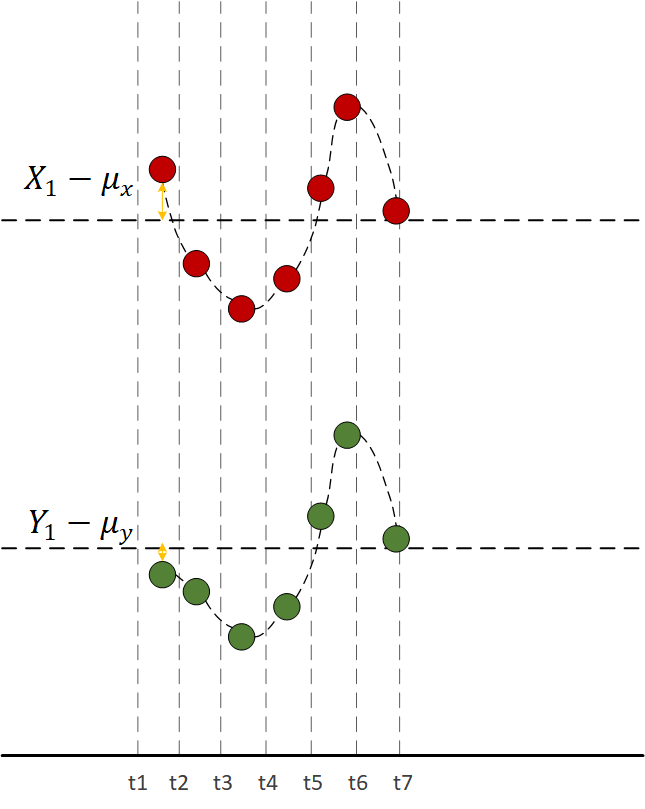
千言不如一图：

        红色代表X变量，绿色代表Y变量，水平虚线代表均值，由图可见，每一时刻 

和  的值的“正负号”一定相同，所以把所有时刻的  和  的乘积加在一起也是正的，说明两个变量是正相关的。

    再来看一个具有实际意义的数据：

        由图可见，商品房的销售面积随着城市化进程的发展而增长，说明两者是正相关的，所以，有的城市为了卖房，会大力搞城市建设，建地铁，搞公园，老城区拆迁等有效措施。

再来一个负相关的例子：

        由图可见，每一时刻  和  的值的“正负号”一定相反，所以把所有时刻的

 和  的乘积加在一起求平均的时候也是负的，说明两个变量是负相关的。

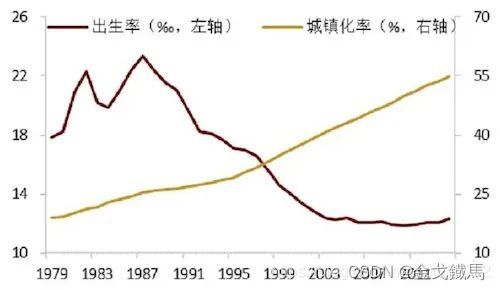
        由图可见，近年来，出生率随着城镇化的加快反而呈下降趋势，这说明在城市养育一个儿童的费用较高，大家在没有赚够钱的情况下不敢生了。

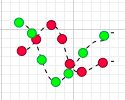
    前面提到的两种情况比较理想，现实中的数据大多是有波动的。

        如上图所示，有时刻的   和  的乘积是负的，有的时刻是正的，讲每个时刻的乘积加在一起，正负就会产生抵消，到底是正相关还是负相关，要取决于最终协方差值的正负与大小。

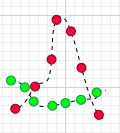
        还有一种情况是，虽然X和Y同向运动，但有的时刻X大于均值，Y却小于均值，他俩的乘积是负的，这与X和Y正相关是矛盾的啊？

        如上图所示，t1时刻，  和   的乘积是负的，但别着急，往后看完，后面6个时刻乘积都是正的，最终结果仍然是正的，所以，总体上看，X和Y仍然是正相关的。

相关系数：

    先从词的组合理解一下这个概念，“相关”貌似与前面的协方差有着某种联系，“系数”这个次我们并不陌生，它代表某种权重，所以相关系数代表着相关性的程度。

    既然已经有了协方差，还要相关系数干什么？因为要对比不同变量之间的相关性，既然是对比，就要要消除量纲的影响，因为不同特征之间的量纲可能是不同的，例如，房屋的价格可能是几千或者几万，房间的个数一般都是在10以内，房屋的面积一般在100左右，如果我们要对比这三者之间的相关性，例如，Cov(房屋的面积，房屋的价格)和Cov(房屋的面积，房间个数)，只计算协方差可能不行，因为不是一个量纲。

        所以，就有了相关系数的概念。

相关系数的公式为：

    用X、Y的协方差除以X的标准差和Y的标准差。这跟我们在数据预处理中的数据标准化是相似的，最终相关系数在-1-1之间，也可以把它看作是一种特殊的协方差。

那它也有以下特性：

1、 也可以反映两个变量变化时是同向还是反向，如果同向变化就为正，反向变化就为负。
2、 由于它是标准化后的协方差，因此重要的特性来了：它消除了两个变量变化幅度的影响，而只是单纯反映两个变量每单位变化时的相似程度。

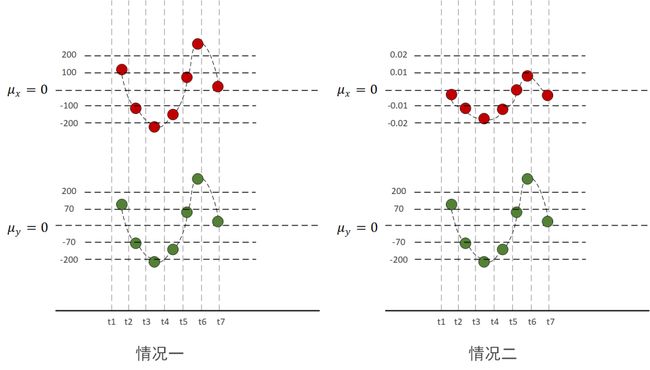
举个例子：

下面我们分别计算上图中的协方差和相关系数来对比一下他们之间的区别。

首先计算它们的协方差：
第一种情况下：

第二种情况下：

    虽然同是正相关，但协方差相差了一万倍，只能从两个协方差都是正数判断出两种情况下X,Y都是同向变化，但是无法对比两种情况下的相关程度。

这是为什么呢？

    因为第一种情况量纲大，量纲大的起到了主导作用，第二种情况会有多个小数相乘，结果会越来越小。

下面计算一下相关系数：

X的标准差为

Y的标准差为

于是相关系数为

    说明第一种情况下，X的变化与Y的变化具有高度的相似性，而且已经接近完全正相关了，X,Y几乎就是线性变化的。

那第二种情况呢？
X的标准差为

Y的标准差为

于是相关系数为

    说明第二种情况下，虽然X的变化幅度比第一种情况X的变化幅度小了10000倍，但是丝毫没有改变“X的变化与Y的变化具有很高的相似度”这一结论。同时，由于第一种、第二种情况的相关系数是相等的，因此在这两种情况下，X,Y的变化过程有着同样的相似度。

    那么为什么要通过除以标准差的方式来剔除变化幅度的影响呢？咱们简单从标准差公式看一下：

    标准差描述了变量在整体变化过程中偏离均值的幅度。协方差除以标准差，也就是把协方差中变量变化幅度对协方差的影响剔除掉，这样协方差也就标准化了，它反应的就是两个变量每单位变化时的情况。这也就是相关系数的公式含义了。

为什么对协方差矩阵进行特征值分解能显示降维？

    在讲矩阵列空间的时候，我们说如果矩阵的某一列是其他列的线性组合，我们就说这些列是线性相关的，举个最简单的例子，第一列是第二列的两倍，那么这两列完全可以去掉其中一列，去掉后并没有丢失什么信息，如果把矩阵当作一种变换，那去掉冗余的列和，其他列所张成的空间维度并不会受影响。

    对协方差矩阵进行特征值分解，就是找到矩阵的变换主方向，这些主方向对应的就是线性无关的列，也就是对通过这些列能张成最大子空间。