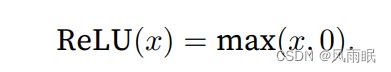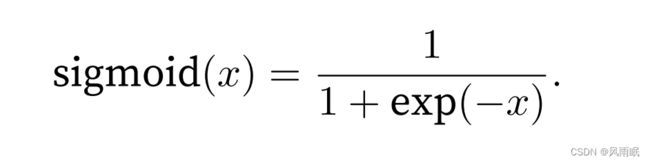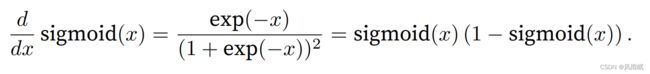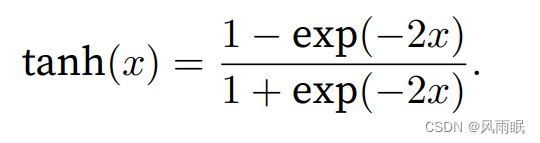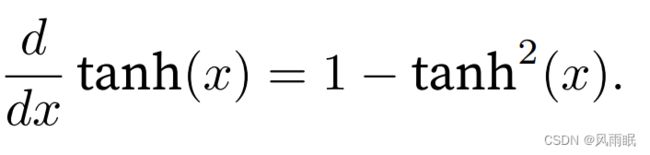多层感知机（MLP）

多层感知器（MLP，Multilayer Perceptron）是一种前馈人工神经网络模型，其将输入的多个数据集映射到单一的输出的数据集上。它最主要的特点是有多个神经元层，因此也叫深度神经网络(DNN: Deep Neural Networks)。

感知机是单个神经元模型，是较大神经网络的前身。神经网络的强大之处在于它们能够学习训练数据中的表示，以及如何将其与想要预测的输出变量联系起来。从数学上讲，它们能够学习任何映射函数，并且已经被证明是一种通用的近似算法。

神经网络的预测能力来自网络的分层或多层结构。而多层感知机是指具有至少三层节点，输入层，一些中间层和输出层的神经网络。给定层中的每个节点都连接到相邻层中的每个节点。输入层接收数据，中间层计算数据，输出层输出结果。
 

一、隐藏层

以通过在网络中加⼊⼀个或多个隐藏层来克服线性模型的限制，使其能处理更普遍的函数关系类型。 要做到这⼀点，最简单的方法是将许多全连接层堆叠在⼀起。每⼀层都输出到上面的层，直到生成最后的输出。我们可以把前L−1层看作表示，把最后⼀层看作线性预测器。

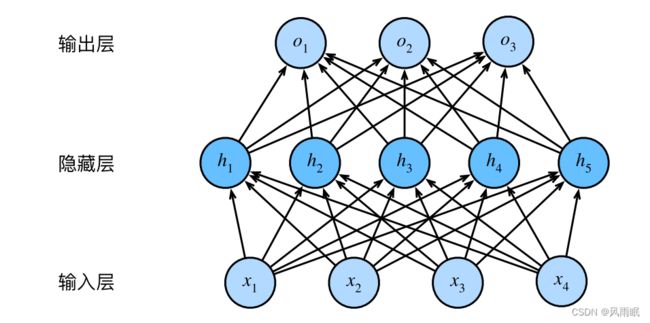上图这个多层感知机有4个输入，3个输出，其隐藏层包含5个隐藏单元。输入层不涉及任何计算，因此使用此网络， 产生输出只需要实现隐藏层和输出层的计算。因此，这个多层感知机中的层数为2。注意，这两个层都是连接的。每个输入都会影响隐藏层中的每个神经元，而隐藏层中的每个神经元又会影响输出层中的每个神经元。

二、激活函数

激活函数（activation function）通过计算加权和并加上偏置来确定神经元是否应该被激活，它们将输⼊信号 转换为输出的可微运算。⼤多数激活函数都是非线性的。

1.ReLU函数

最受欢迎的激活函数是修正线性单元（Rectified linear unit，ReLU），因为它实现简单，同时在各种预测任务 中表现良好。ReLU提供了⼀种⾮常简单的非线性变换。给定元素x，ReLU函数被定义为该元素与0的最大值：

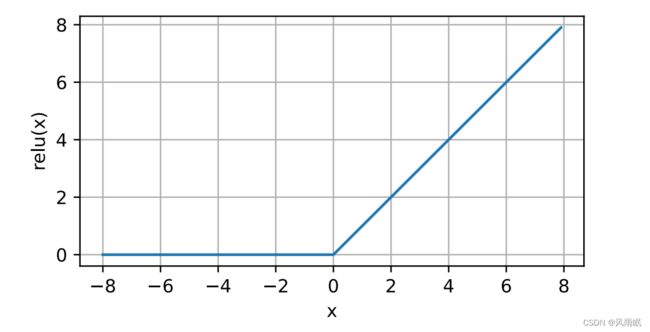
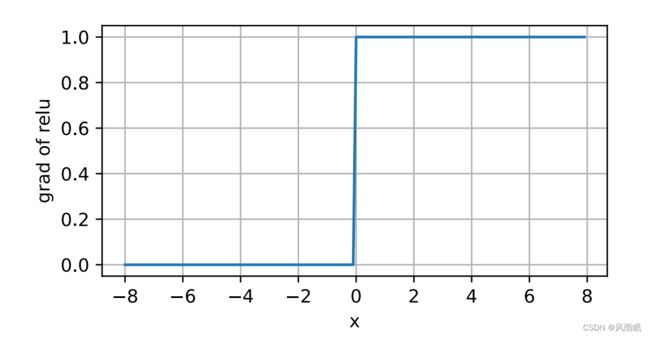
通俗地说，ReLU函数通过将相应的活性值设为0，仅保留正元素并丢弃所有负元素。当输⼊为负时，ReLU函数的导数为0，当输⼊为正时，ReLU函数的导数为1。注意，当输⼊值精确等于0时， ReLU函数不可导。在此时，我们默认使⽤左侧的导数，即当输⼊为0时导数为0。我们可以忽略这种情况，因 为输⼊可能永远都不会是0。

x = torch.arange(-8.0, 8.0, 0.1, requires_grad=True)
y = torch.relu(x)
d2l.plot(x.detach(), y.detach(), 'x', 'relu(x)', figsize=(5, 2.5))

使⽤ReLU的原因是，它求导表现得特别好：要么让参数消失，要么让参数通过。这使得优化表现得更好，并 且ReLU减轻了困扰以往神经⽹络的梯度消失问题。

y.backward(torch.ones_like(x), retain_graph=True)
d2l.plot(x.detach(), x.grad, 'x', 'grad of relu', figsize=(5, 2.5))

2.sigmoid函数

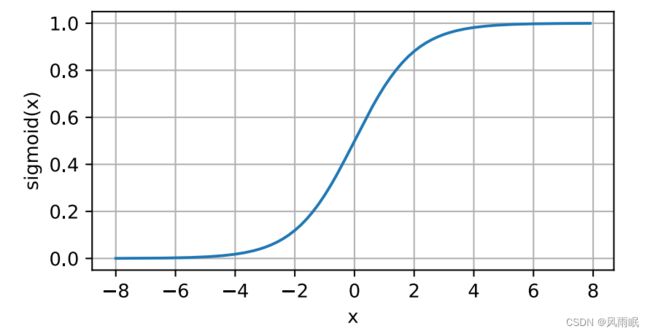
对于⼀个定义域在R中的输⼊，sigmoid函数将输⼊变换为区间(0, 1)上的输出。因此，sigmoid通常称为挤压 函数（squashing function）：它将范围（-inf, inf）中的任意输⼊压缩到区间（0, 1）中的某个值：

 

y = torch.sigmoid(x)
d2l.plot(x.detach(), y.detach(), 'x', 'sigmoid(x)', figsize=(5, 2.5))

sigmoid函数的导数为下⾯的公式：

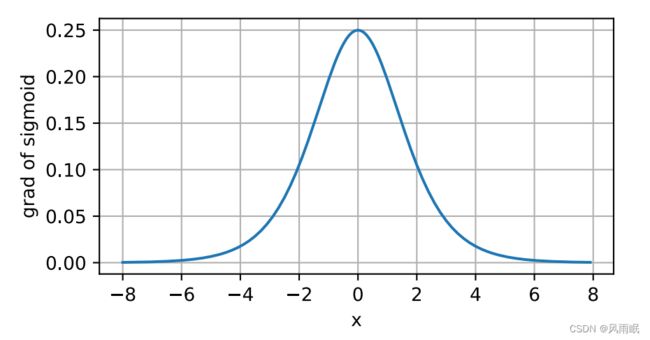
sigmoid函数的导数图像如下所⽰。注意，当输⼊为0时，sigmoid函数的导数达到最⼤值0.25；⽽输⼊在任⼀ ⽅向上越远离0点时，导数越接近0。 

# 清除以前的梯度
x.grad.data.zero_()
y.backward(torch.ones_like(x),retain_graph=True)
d2l.plot(x.detach(), x.grad, 'x', 'grad of sigmoid', figsize=(5, 2.5))

 

3.tanh函数

与sigmoid函数类似，tanh(双曲正切)函数也能将其输⼊压缩转换到区间(-1, 1)上。tanh函数的公式如下：

当输⼊在0附近时，tanh函数接近线性变换。函数的形状类似于sigmoid函数， 不同的是tanh函数关于坐标系原点中⼼对称。

y = torch.tanh(x)
d2l.plot(x.detach(), y.detach(), 'x', 'tanh(x)', figsize=(5, 2.5))

 

 

tanh函数的导数是：

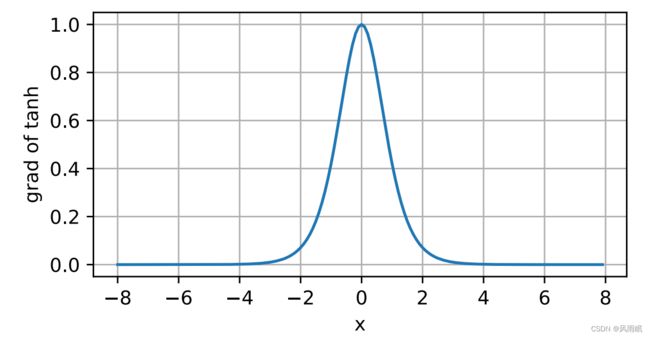
 tanh函数的导数图像如下所⽰。当输⼊接近0时，tanh函数的导数接近最⼤值1。与我们在sigmoid函数图像 中看到的类似，输⼊在任⼀⽅向上越远离0点，导数越接近0。

# 清除以前的梯度
x.grad.data.zero_()
y.backward(torch.ones_like(x),retain_graph=True)
d2l.plot(x.detach(), x.grad, 'x', 'grad of tanh', figsize=(5, 2.5))

 参考：多层感知机（MLP）_DeeGLMath的博客-CSDN博客

             https://zh-v2.d2l.ai/d2l-zh-pytorch.pdf