最短路径算法python（一）（Floyd--弗洛伊德）

目录

前言

一、Floyd算法图文解析

二、找到最短路径的算法

三、完整代码

总结

---

前言

这段时间会出一些数学建模题的思路和解法，因为最近准备建模，先放放爬虫晚一些些有空了再发哈（其实后面也没什么了，scrapy框架爬取其实相差无几还是老套路，然后就是js逆向，这里推荐看看这个作者的文章我也在学）

---

一、Floyd算法图文解析

路径图（晚点补上）--->表

列表示从某点到某点的权（理解为距离也行但是不是距离看你输入的单位是什么）

如果不能直接连接即设置为无限大python表示为float('inf') 即可 这里我用10086表示最大值

 核心算法就是：

path 初始化路径

A      上表二维表

v       v是开始的点（从点0开始 v=0，从点1开始v=1）

大致看一下就好 然后直接看下面的式子： 

对于每个顶点V，和任一顶点对的（i，j），i≠j，v≠i，v≠j

如果A[i][j] > A[i][v] + A[v][j],则将A[i][j]更新为A[i][v] + A[v][j]的值，并将path[i][j]改为v

通俗的说就是：

例如 假设从V1点开始出发，（v=1）看表点（1）到点（4）的距离为Max

而从点V1->V2->V4: Max > 5+4 

整个式子就是           A【0】【3】> A【0】【1】+A【1】【3】

所以就要对A赋值：【0】【3】 = A【0】【1】+A【1】【3】

一整个就是按照这个去对着图看很简单的思路 狗都会那种

下面就是核心算法：

    for i in range(len(array_data)):
        for j in range(len(array_data)):
            path_k[i][j] = -1
    for k in range(len(array_data)):
        for i in range(len(array_data)):
            for j in range(len(array_data)):
                if array_data[i][j] > array_data[i][k] + array_data[k][j]:
                    array_data[i][j] = array_data[i][k] + array_data[k][j]
                    path_k[i][j] = k

二、找到最短路径的算法

在上面我们会得到一个新的path（就是计算后的路径）

 计算后的path的值：

例如我想从1到6：

path【0】【5】 = 1

path【1】【6】 = 4

path【4】【6】 = 0

路径就为：0-->1-->4-->6

这里停三分钟悟一下 理一下整体思路就可以去写代码了

核心算法：

这里的mid就是中间点 再从中间点到目标点（结合红字上面的推导就很清楚的）

    if new_path[start][end] == 0:
        all+=num[start][end]
        print(f'{start}---->{end}')
        return
    else:
        mid = path[start][end]
        find_small(new_path,start,mid)
        find_small(new_path,mid,end)

运行结果

从v1 到 v6的计算的最短路径：

 

 

三、完整代码

import numpy as np
from pprint import pprint
inf = 10086
num =  [[0,4,6,inf,inf,inf],
        [inf,0,inf,5,4,inf],
        [inf,inf,0,4,7,inf],
        [inf,inf,inf,0,5,7],
        [inf,inf,inf,inf,0,5],
        [inf,inf,inf,inf,inf,0]]
# print(np.array(num) <= 7)
path = np.zeros((len(num),len(num)))
for i in range(len(num)):
    for j in range(len(num)):
        if num[i][j] == inf:
            path[i][j] = inf
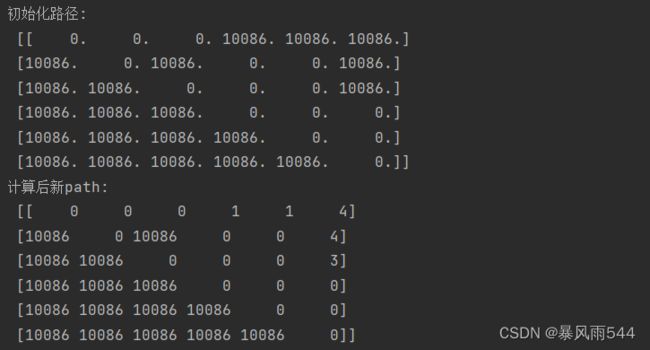
print('初始化路径:\n',path)
# pprint(num)

def floyd(array_data,path_k):

    for i in range(len(array_data)):
        for j in range(len(array_data)):
            if path_k[i][j] != inf:
                path_k[i][j] = 0
    for k in range(len(array_data)):
        for i in range(len(array_data)):
            for j in range(len(array_data)):
                if array_data[i][j] > array_data[i][k] + array_data[k][j]:
                    array_data[i][j] = array_data[i][k] + array_data[k][j]
                    path_k[i][j] = k
    # pprint(array_data)
    return path_k
ne_path = floyd(num,path)
for i in range(len(num)):
    for j in range(len(num)):
        if num[i][j] == inf:
            ne_path[i][j] = inf
print('计算后新path:\n',np.array(ne_path,dtype=int))
all = 0
def find_small(new_path,start,end):
    global all
    start = int(start)
    end = int(end)
    if new_path[start][end] == 0:
        all+=num[start][end]
        print(f'{start}---->{end}')
        return
    else:
        mid = path[start][end]
        find_small(new_path,start,mid)
        find_small(new_path,mid,end)
find_small(ne_path,0,5)

总结

最好不要用float('inf')作为最大值吧 因为后面要转int好像不太行（当然也可以写一个判断去跳过这个索引也行）

还有好像有人说c语言里面的无线大乘还是加会变成无限小，总之用一个具体的极大值比较稳