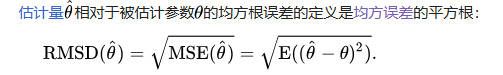光谱图像常见评价指标

光谱图像常见评价指标

SAM（Spectral Angle Mapper）

​ SAM算法是由Kruse等[146]在1993年提出，把图像中的每个像元的光谱视为一个高维向量，通过计算两向量间的夹角来度量光谱间的相似性，夹角越小，两光谱越相似，属于同类地物的可能性越大，因而可根据光谱角的大小来辨别未知数据的类别。分类时，通过计算未知数据与已知数据间的光谱角，并把未知数据的类别归为最小光谱角对应的类别中。
$$SAM=co{s}^{-1}(\frac{Y^{T}X}{||Y||||X||})$$
其中 Y 是给定的目标向量，X 是要测量的向量。

# Loss_SAM 类定义了结构相似性（SAM）的损失函数。
# forward 方法接受两个输入图像（im1 和 im2）作为输入。
# 函数首先确保两个图像具有相同的形状，然后进行一系列操作以计算结构相似性（SAM）。
# 结构相似性度量被计算为两个输入图像之间的平均值，并作为输出返回。
# 请注意，此实现中使用了 NumPy 而不是 PyTorch 张量，您可能需要将其转换为 PyTorch 操作以使其适用于深度学习模型的训练。
class Loss_SAM(nn.Module):
    def __init__(self):
        super(Loss_SAM, self).__init__()
        #一个正则项，添加到分母和分子中，以防止除以零或对接近 1 的值取反余弦函数。
        self.eps = 2.2204e-16

    def forward(self, im1, im2):
        assert im1.shape == im2.shape
        H, W, C = im1.shape
        im1 = np.reshape(im1, (H * W, C))
        im2 = np.reshape(im2, (H * W, C))
        core = np.multiply(im1, im2)
        mole = np.sum(core, axis=1)
        im1_norm = np.sqrt(np.sum(np.square(im1), axis=1))
        im2_norm = np.sqrt(np.sum(np.square(im2), axis=1))
        deno = np.multiply(im1_norm, im2_norm)
        sam = np.rad2deg(np.arccos(((mole + self.eps) / (deno + self.eps)).clip(-1, 1)))
        return np.mean(sam)

1. 对于$x_i^T{x}^{\ast }$，相当于对这两个向量进行点积然后再进行求和。den=np.sum(np.dot(im1,im2))

2. 内积为向量与转置的乘积。

     im1_norm = np.sqrt(np.sum(np.square(im1), axis=1))
     im2_norm = np.sqrt(np.sum(np.square(im2), axis=1))
     deno = np.multiply(im1_norm, im2_norm)
   

RMSE——Root Mean Square Error

# Loss_RMSE 类定义了均方根误差（RMSE）的损失函数。
# forward 方法接受输出（outputs）和标签（label）作为输入。
# 函数首先确保输出和标签具有相同的形状，然后计算它们之间的均方根误差（RMSE）。

class Loss_RMSE(nn.Module):
    def __init__(self):
        super(Loss_RMSE, self).__init__()

    def forward(self, outputs, label):
        assert outputs.shape == label.shape
        error = outputs.clamp(0., 1.) * 255 - label.clamp(0., 1.) * 255
        sqrt_error = torch.pow(error, 2)
        rmse = torch.sqrt(torch.mean(sqrt_error.contiguous().view(-1)))
        return rmse

1. outputs.clamp(0., 1.) * 255 - label.clamp(0., 1.) * 255将数值映射到（0-1），并放到到255，因为图像中的像素值通常是0-255的数值

2. ${\sum }_{i=1}^n{\left(Y_i-f\left(x_i\right)\right)}^2$对平方误差进行求平均值，

   其中.contiguous(): 这是一个方法调用，通常用于确保张量在内存中的布局是连续的。在某些情况下，PyTorch张量可能不是连续的，这可能会导致一些计算问题。.contiguous() 方法将确保张量的内存布局是连续的。.view(-1): 这是一个形状变换操作。它将张量重新整形为一维张量，其中"-1" 表示根据张量的大小自动推断新的形状。这通常用于将多维张量展平为一维，以便进行后续计算或操作。

PSNR

峰值信噪比 (PSNR) 是最流行的图像质量评估指标之一。然而 PSNR 侧重于像素差异，并且仅与两者的 MSE 相关，因此在表示现实世界 SR 重建的质量方面往往表现不佳。

# Loss_PSNR 类定义了计算峰值信噪比（PSNR）的损失函数。
# forward 方法接受真实图像（im_true）和生成图像（im_fake）作为输入。
# data_range 参数用于指定数据范围，默认为255。
# 函数首先将输入图像缩放到指定数据范围，然后计算图像之间的均方差误差（err）。
# 最后，通过计算 PSNR 并返回平均 PSNR 值。
class Loss_PSNR(nn.Module):
    def __init__(self):
        super(Loss_PSNR, self).__init__()

    def forward(self, im_true, im_fake, data_range=255):
        Itrue = im_true.clamp(0., 1.) * data_range
        Ifake = im_fake.clamp(0., 1.) * data_range
        err = Itrue - Ifake
        err = torch.pow(err, 2)
        err = torch.mean(err, dim=0)
        err = torch.mean(err, dim=0)

        psnr = 10. * torch.log10((data_range ** 2) / err)
        psnr = torch.mean(psnr)
        return psnr

SSIM

结构相似性指标[1]（英语：structural similarity index，SSIM index）是一种用以衡量两张数字图像相似程度的指标。当两张图像其中一张为无失真图像，另一张为失真后的图像，二者的结构相似性可以看成是失真图像的图像质量衡量指标。相较于传统所使用的图像质量衡量指标，像是峰值信噪比（英语：PSNR），结构相似性在图像质量的衡量上更能符合人眼对图像质量的判断[2][3]

由于人类的主观感知对观察对象的结构很敏感，研究人员提出了结构相似性 (SSIM) [25] 指数来衡量标记图像和重建图像之间的结构相似性。对于图像I的亮度μI和对比度σI，它们是根据图像强度的平均值和标准差来估计的

from skimage.metrics import structural_similarity as compare_ssim
 SSIM = compare_ssim(X=x_true, Y=x_pred)

MSSIM

MSSIM用于计算两幅高光谱图像之间的平均结构相似度。MSSIM计算方法很简单，只需要分别计算不同波段的SSIM指数，取均值就可以了。

def mssim(x_true,x_pred):
    """
        :param x_true: 高光谱图像：格式：(H, W, C)
        :param x_pred: 高光谱图像：格式：(H, W, C)
        :return: 计算原始高光谱数据与重构高光谱数据的结构相似度
    """
    SSIM = compare_ssim(X=x_true, Y=x_pred, multichannel=True)
    return SSIM

EGARS

ERGAS（全称：Normalized Global Error (ERGAS)）是一种用于评估遥感图像质量的指标。它通常用于评估图像处理或压缩算法的性能，以及遥感图像的质量，特别是在图像压缩、图像增强和图像恢复等领域中。

ERGAS的计算公式如下：

E R G A S = 1 N ∑ i = 1 N ( 100 L 1 M S E i ∑ j = 1 L ( R M S E i j Y i ) 2 ) ERGAS = \sqrt{\frac{1}{N} \sum_{i=1}^{N} \left( \frac{100}{L} \sqrt{\frac{1}{MSE_i} \sum_{j=1}^{L} \left(\frac{RMSE_{ij}}{Y_i}\right)^2}\right)} ERGAS=N1​i=1∑N​ ​L100​MSEi​1​j=1∑L​(Yi​RMSEij​​)2 ​ ​ ​
其中，

• N表示图像的波段数；
• L表示图像的灰度级数；
• $MS{E}_i$是第i个波段的均方误差（Mean Squared Error）；
• $RMS{E}_{ij}$是第i个波段中第j个像素的均方根误差（Root Mean Squared Error）；
• $Y_i$是第i个波段的平均亮度。

ERGAS的值通常以百分比表示，越低的ERGAS值表示图像质量越高。ERGAS主要用于比较不同图像处理算法或压缩方法的性能，以确定它们对图像质量的影响。

总的来说，ERGAS是一种用于评估遥感图像质量的定量指标，它考虑了图像的均方误差、均方根误差以及亮度信息，以提供对图像处理或压缩算法性能的综合评估。

import numpy as np

# 定义一个函数来计算ERGAS
def calculate_ergas(reference_image, processed_image):
    # 获取图像的尺寸
    height, width, num_bands = reference_image.shape

    # 初始化变量用于计算各个波段的MSE和RMSE
    mse_values = []
    rmse_values = []

    for band in range(num_bands):
        # 计算MSE（均方误差）
        mse = np.mean((reference_image[:, :, band] - processed_image[:, :, band]) ** 2)
        mse_values.append(mse)

        # 计算RMSE（均方根误差）
        rmse = np.sqrt(mse)
        rmse_values.append(rmse)

    # 计算每个波段的平均亮度
    average_brightness = [np.mean(reference_image[:, :, band]) for band in range(num_bands)]

    # 定义常数参数
    N = num_bands
    L = 256  # 假设灰度级数为256

    # 计算ERGAS
    ergas_values = []
    for mse, rmse, Y in zip(mse_values, rmse_values, average_brightness):
        ergas_values.append((100 / L) * np.sqrt(1 / mse) * (rmse / Y) ** 2)
    
    ergas = np.sqrt((1 / N) * np.sum(ergas_values))

    return ergas

# 示例用法
if __name__ == "__main__":
    # 假设有两遥感图像：reference_image为参考图像，processed_image为经过处理的图像
    # 这里使用随机生成的示例图像数据，您应该替换为实际数据
    height, width, num_bands = 100, 100, 3
    reference_image = np.random.rand(height, width, num_bands)
    processed_image = np.random.rand(height, width, num_bands)

    # 计算ERGAS值
    ergas_value = calculate_ergas(reference_image, processed_image)
    print(f"ERGAS值为: {ergas_value}")