算法设计与分析——算法分析基础
算法分析主要是时间复杂度和空间复杂度的两个方面的分析
此处带着问题小预告一把：
时间复杂度？空间复杂度？
大O、大
和大
分别表示什么？
如何得到递归方程？如何求解递归方程呢？
带着问题来探索吧~
目录
算法分析主要是时间复杂度和空间复杂度的两个方面的分析
一、时间复杂度分析
1.事后实验统计法——编写算法对应程序，统计其执行时间
2.事前分析估算法——渐近分析法（重点）
3.大O符号——渐近上界记号
4.大Ω符号——渐近下界记号
5.大符号——渐近紧界记号
6.渐近记号性质
重要结论：
二、渐近空间复杂度分析
定义：
三、递归算法复杂度分析
1. 建立递归方程
2. 求解该递归方程
一、时间复杂度分析
1.事后实验统计法——编写算法对应程序，统计其执行时间
利用计算机内的计时功能，编写算法对应程序，统计其执行时间。
对硬件、软件环境依赖强，不同的电脑设备对同一算法程序所得结果可能有一些偏差。
同一个算法用不同的语言、不同的编译程序、在不同的计算机上运行，效率均不同——— 使用绝对时间单位衡量算法效率不合适（没办法，你的软硬件环境就是在里面起着一定作用。）
2.事前分析估算法——渐近分析法（重点）
所谓的渐近分析是指忽略具体机器、编程语言和编译器的影响，只关注在输入规模增大时算法运行时间的增长趋势。
1）算法的运行时间是问题规模n的函数，记作T(n)
2）用基本语句的执行次数表示T(n)
3）忽略低阶项和常系数，只考虑最高阶
4）用大O、大和大表示其渐近意义下的阶
时间复杂度是由嵌套最深层语句的频度决定的
3.大O符号——渐近上界记号
1）定义：如果存在两个正的常数c和n0，对于任意n≥n0，都有f(n)≤c×g(n)，则记为f(n)=O(g(n)),即g(n)为f(n)的上界。
2）图助理解
大O符号用来描述增长率的上界，表示f(n)的增长率≤g(n)的增长率。即当输入规模为n时， g(n)为算法消耗时间的最大值
3）上界g(n)的阶越低，评估越准确，结果越有价值，通常将这个最有价值的g(n)称之为f(n)的“紧凑上界”或“紧确上界”。
4）例题：
5）总结：一般的，如果f(n)=
, 有f(n) = O(
)。
4.大Ω符号——渐近下界记号
1）定义：若存在两个正的常数c 和n0，对于任意n≥n0，都有f(n)≥c×g(n)，则称f(n)=Ω(g(n)),即g(n)为f(n)的下界。
2）图助理解
大符号用来描述增长率的下界，表示f(n)的增长率≥g(n)的增长率，即当输入规模为n时， g(n)为算法消耗时间的最小值。
3）下界g(n)的阶越高，评估越准确，结果越有价值，通常将这个最有价值的g(n)称为f(n)的“紧凑下界”或“紧确下界”。
4）例题：
5）总结：一般的，如果f(n)= , 有f(n) = ()。
5.大符号——渐近紧界记号
1）定义：若存在三个正的常数c1、c2和n0，对于任意n≥n0都有c1×g(n)≥f(n)≥c2×g(n)，则称f(n)=(g(n))，即g(n)与f(n)同阶。
2）图助理解
f(n)=(g(n))，当且仅当f(n)=O(g(n))，f(n)=(g(n))
3）例题：
4）总结： 一般的，如果f(n)= , 有f(n) = ()。
6.渐近记号性质
重要结论：
法则1：如果T1(n)=O(f(n))，T2(n)=O(g(n)),那么
(a) T1(n)+T2(n)= O(f(n)+g(n)) (也可以写成 O(max(f(n),g(n)))
为什么这里的加和选最大可以等价呢，因为渐进分析法忽略低阶项和常系数，只考虑最高 阶，所以加起来取最高阶和直接选最高阶结果一样。
(b) T1(n)*T2(n)= O(f(n)*g(n))
法则2：对任意常数k，
≤ O(n)。 （说明n的增长要快于log2n的任意次幂）
法则3：若T（n）= (
>0),则有T（n）=O（) 且 T（n）=（），因此有 f(n) = ()。
常见函数的阶
- 多项式阶算法（有效算法）：T(n)=O(
) - 常见的多项式阶有
- 指数阶算法： T(n)= (
),a>1 - 常见的指数阶有
小例题练练手~
【例5】 求下列算法的时间复杂度
void InsertSort(SqList ＆L)
{ int i,j;
for(i=2;i<=L.length; i++)
{ if( L.R[i].key=L.R[j].key))
L.R[j+1]=L.R[0]; //插入到正确位置
}
}
}
参考解答：
二、渐近空间复杂度分析
定义：
一个算法的存储量包括形参所占空间和临时变量所占空间。在对算法进行存储空间分析时，只考察临时变量所占空间。
空间复杂度是对一个算法在运行过程中临时占用的存储空间大小的量度，一般也作为问题规模n的函数，以数量级形式给出，记作：
S(n)=O(g(n))、(g(n))或(g(n))
其中渐进符号的含义与时间复杂度中的含义相同。
小例子理解一下~
如果算法所需的辅助空间相对于问题的输入规模来说是一个常数，我们称此算法为原地（或就地）工作。
为什么算法占用的空间只考虑临时空间，而不必考虑形参的空间呢？
这是因为形参的空间会在调用该算法的算法中考虑，例如，以下maxfun算法调用上面的max算法：
maxfun算法中为b数组分配了相应的内存空间，其空间复杂度为O(n)，如果在max算法中再考虑形参a的空间，这样重复计算了占用的空间。
三、递归算法复杂度分析
1. 建立递归方程
递归方程是一个等式或不等式，它通过更小的输入上的函数值来描述一个函数。
当一个算法包含对其自身的递归调用时，可以用递归方程来表示其运行时间
例1.建立算法的递归方程
void Hanoi(int n,char A,char B,char C)
{ if (n==1)
printf("将盘片%d从%c搬到%c\n“,n,A,C);
else
{ Hanoi(n-1,A,C,B);
printf("将盘片%d从%c搬到%c\n",n,A,C);
Hanoi(n-1,B,A,C);
}
}
参考解答(前面的代表括号，嘻嘻~）：
/T(n) = O(1) 当n=1时
\T(n) = 2T(n-1)+O(1) 当n>1时
例2.请给出斐波那契数列的递归算法并建立算法的递归方程
int Fib(int n)
{
if (n==0 || n==1)
return n;
else
{ int x=Fib(n-1);
int y=Fib(n-2);
return x+y;
}
}
参考解答：
/T(n)=O(1) 当n=1
\T(n)=T(n-1)+T(n-2)+O(1) 当n>1
例3.建立算法的递归方程
int maxelem(int a[],int i,int j)
{ int mid=(i+j)/2,max1,max2;
if (imax2)?max1:max2;
}
else return a[i];
}
参考解答：
/T(n)=O(1) 当n=1
\T(n)=2T(n/2)+O(1) 当n>1
这一步很简单，从例子中找到他的解法规则吧~你一定可以的！
2. 求解该递归方程
1）迭代法
从初始递归方程开始，反复用递归方程右边的等式代入左边的函数，直到得到初值。
小例子走起~
________________________________________
求解递归方程
T(n) = O(1) 当n=1时
T(n) = 2T(n/2)+ O(n) 当n>1时
参考解答:
T(n) = 2T(n/2)+cn
=2*[2T(n / 
)+cn/2]+cn
= * T(n / )+2cn
= 
* T(n / )+3cn
= …
= 
* T(n / )+kcn //这里假设n=2^k，则k=
(重要处理思路！）
= nO(1)+cnlog2n=n+cn
= O(n)
2）代入法
猜测解的形式；用数学归纳法证明（还是来一个例子，这个方法用的少）
例.求解递归方程 T(n) = 2T(n/2+5)+ n
用代入法求解 （1）猜测解的形式：T(n)=O(n)
（2）用数学归纳法求出解中的常数，并证明解是正确的
3）递归树法
- 展开递归方程，构造对应的递归树
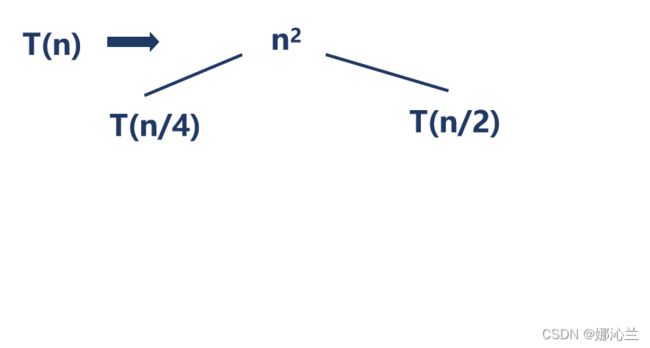
递归树的构造方法 递归树是一棵结点带权值的树，每个结点表示一个单一子问题的代价，子问题对应某次递归函数调用。 初始的递归树只有一个结点，它的权标记为T(n)；然后按照递归树的迭代规则不断进行迭代，每迭代一次递归树就增加一层，直到树中不再含有权值为函数的结点。
- 将树中每层中的代价求和，得到每层代价，再将所有层的代价求和，得到总的递归调用代价
小例子再次走起~
________________________________________
解答（图片演示~）：
4）主方法
主方法适用于求解下面的递归形式：
其中a≥1，b>1为常数， f(n)为渐近正函数
先来将抽象的递归式进行展开
小例子再再次走起~
________________________________________
求解递归方程 T(n)=4T(n/2)+O(n)
对于红色部分，主方法无能为力