希尔排序详解

希尔排序是希尔（Donald Shell）于1959年提出的一种排序算法。希尔排序也是一种插入排序，它是简单插入排序经过改进之后的一个更高效的版本，也称为缩小增量排序（Diminishing Increment Sort）。

1 希尔排序的思想

希尔排序与简单插入排序的不同是希尔排序先对数据进行了分组，再在组内分别进行插入排序，排序完再对数据分成更小的组在进行排序，直到组内只有1个元素的简单插入排序。

2 希尔排序的特点

希尔排序是在简单插入排序的基础上改进而来的，利用了插入排序在以下情况下表现较好的特点：

（1）如果序列元素在未排序前就已经接近有序，那么能够极大简化比较和插入的过程；

（2）若如果序列的长度较小，则插入操作也较少（插入排序的平均时间复杂度为O(n^2)，最好为O(n)，当n较小，那么也会比较接近最好时间复杂度）

希尔排序不仅通过分组实现了较小的序列长度，而且因为每次分组排序使得大多数元素已经接近有序，越往后排序的阻力会减小。

3 增量

希尔排序的分组是根据增量Increment安排的，即increment个数分为一组，在数据中变现为每increment个数取一个划为一组。

每次分组增量都在递减，递减的规律没有特别规定一般是取increment为数据长度length的一半，再不断减半到为1。

4 希尔排序的具体过程

（1）假设要做升序排序，要处理的数据有length=10个数，一般会取增量的初始值为length/2=5，即分为5组，每5个数取1个，组内相邻两个数间隔4个数。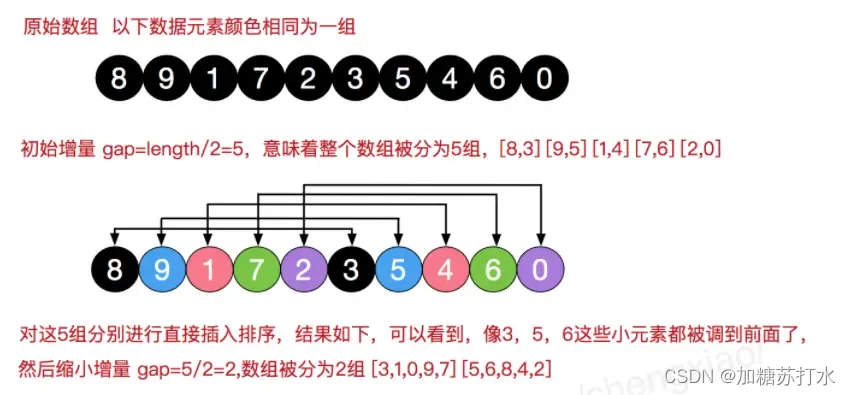

 （2）对5个组内的数据分别进行插入排序，组内的第一个数作为有序列表的初始元素，把后面的元素插进来，那么在这里对于第一组就是第6个数“3”与第1个数“8”相比小，所以把3与8的位置交换。同理对各个组进行操作。

（3）接着进行第二次分组，此时increment减半，为2。这时对于第一组需要把第3,5,7,9的元素插进来，第二组把第4,6,8,10的数插进来。

（4）最后一次分组，increment已经为1，就是简单插入排序。

 5 希尔排序的代码解读（java）

public static int[] insertSort (int[] arr){
        //设置增量，增量递减，增量数代表有多少组，也代表每增量数取一个数
        for(int increment = arr.length / 2;increment >= 1;increment = increment / 2){
            //i是待插入的数据，从increment开始是因为留出每组的首个元素作为有序列表不需要操作，i每+1都会变换到另一个组进行插入排序
            for(int i = increment;i < arr.length;i++){
                int index = i;//arr[index-increment]代表改组待插入元素前的元素
                while(index - increment >= 0 && arr[index] < arr[index - increment]){
                    int temp = arr[index];
                    arr[index] = arr[index - increment];
                    arr[index - increment] = temp;
                    index--;
                }
            }
        }
        return arr;
    }

 主要的结构就是两层for循环和一层while循环。第一层for很好理解，就是划分不同的增量increment，对应几次分组；while循环如果已经弄懂简单插入排序也很好理解，只是数据间隔改为increment而已；

我在学希尔排序花了很长时间才搞懂的是第二层for循环，它是怎么针对不同组别来做插入排序的。首先需要接受的概念是：

（1）每组的首个元素作为有序列表的初始元素，是不需要操作的

（2）插入排序是把后面的元素不断插到在前面的有序序列中

（3）每次排序一共有increment组而且，组内的每个元素是按每increment取一个取出来的

所以待插入的数据i从increment开始是把increment个组的首个元素留出来，后面的才是需要插入的数据，然后i每自增1其实都会变换要插入的组，直到把从increment到length的数据全都插完。

6 希尔排序的时间复杂度

希尔排序的时间复杂度计算比较复杂，不展开细说，普遍认为希尔排序的平均时间复杂度为O(n^1.3)并介于最好O(n)和最差O(n^2)之间。

并且由于在不同小组做插入排序时有较大幅度地变换数据的位次的可能性，所以希尔排序是不稳定的。

图片参考【尚硅谷】数据结构与算法（Java数据结构与算法）