目标检测---NMS代码实现（python）

目标检测—NMS代码实现（python）

思路分析

非极大值抑制(Non-Maximum Suppression,NMS)，顾名思义就是抑制不是极大值的元素，可以理解为局部最大搜索。是目标检测中常用的一种精修bounding box的方式。

上面就很好的展示了NMS的运行效果~

1.首先输入图片中包括很多目标种类（人，马，狗，汽车）。
2.可以通过各式各样的候选框生成方法，可以得到右上角图中众多候选框（目前还没有进行分类）。
3.到了右下角图中，每个类别都用不同的颜色进行标注，但是每个类别都有很多重叠的候选框。
4.最后，我们就可以通过NMS算法进行筛选，最终得到了分类器认为置信度最高的框作为最后的预测框。

下面简单的举个例子来说明下NMS的算法过程

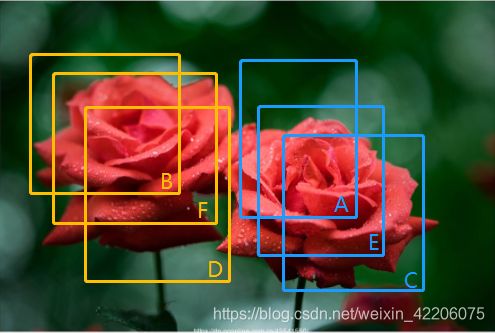
上图假设通过某种候选框生成方法生成了6个候选框，假设从小到大属于花的概率分别为A=0.4、B=0.5、C=0.6、D=0.7、E=0.8、F=0.9；

1.从最大概率矩形框F开始，分别计算A~E与F的重叠度IOU是否大于某个设定的阈值。
2.假设B、D与F的重叠度超过阈值，那么就删除B、D；并标注F矩形框保留下来。
3.从剩下的A、C、E中，选择概率最大的E，然后判断E与A、C的重叠度，重叠度大于阈值，则删除，并标记E为保留下来的第二个矩形框。
4.从剩下的A、C、E中，选择概率最大的E，然后判断E与A、C的重叠度，重叠度大于阈值，则删除，并标记E为保留下来的第二个矩形框

代码实现

boxes = np.array([[100, 100, 210, 210, 0.72],
                  [250, 250, 420, 420, 0.8],
                  [220, 220, 320, 330, 0.92],
                  [100, 100, 210, 210, 0.72],
                  [230, 240, 325, 330, 0.81],
                  [220, 230, 315, 340, 0.9]])

def py_cpu_nms(dets, thresh):
    # 首先数据赋值和计算对应矩形框的面积
    # dets的数据格式是dets[[xmin,ymin,xmax,ymax,scores]....]

    x1 = dets[:, 0]
    y1 = dets[:, 1]
    x2 = dets[:, 2]
    y2 = dets[:, 3]
    areas = (y2 - y1 + 1) * (x2 - x1 + 1)
    scores = dets[:, 4]
    print('areas  ', areas)
    print('scores ', scores)

    # 这边的keep用于存放，NMS后剩余的方框
    keep = []

    # 取出分数从大到小排列的索引。.argsort()是从小到大排列，[::-1]是列表头和尾颠倒一下。
    index = scores.argsort()[::-1]
    print('index:',index)
    # 上面这两句比如分数[0.72 0.8  0.92 0.72 0.81 0.9 ]
    #  对应的索引index[  2   5    4     1    3   0  ]记住是取出索引，scores列表没变。

    # index会剔除遍历过的方框，和合并过的方框。
    while index.size > 0:
        print(index.size)
        # 取出第一个方框进行和其他方框比对，看有没有可以合并的
        i = index[0]  # 取出第一个索引号，这里第一个是【2】

        # 因为我们这边分数已经按从大到小排列了。
        # 所以如果有合并存在，也是保留分数最高的这个，也就是我们现在那个这个
        # keep保留的是索引值，不是具体的分数。
        keep.append(i)
        print('keep:',keep)
        print('x1:', x1[i])
        print(x1[index[1:]])

        # 计算交集的左上角和右下角
        # 这里要注意，比如x1[i]这个方框的左上角x和所有其他的方框的左上角x的
        x11 = np.maximum(x1[i], x1[index[1:]])  # calculate the points of overlap
        y11 = np.maximum(y1[i], y1[index[1:]])
        x22 = np.minimum(x2[i], x2[index[1:]])
        y22 = np.minimum(y2[i], y2[index[1:]])
        print('*'*20)
        print(x11, y11, x22, y22)
        # 这边要注意，如果两个方框相交，X22-X11和Y22-Y11是正的。
        # 如果两个方框不相交，X22-X11和Y22-Y11是负的，我们把不相交的W和H设为0.
        w = np.maximum(0, x22 - x11 + 1)
        h = np.maximum(0, y22 - y11 + 1)

        # 计算重叠面积就是上面说的交集面积。不相交因为W和H都是0，所以不相交面积为0
        overlaps = w * h
        print('overlaps is', overlaps)

        # 这个就是IOU公式（交并比）。
        # 得出来的ious是一个列表，里面拥有当前方框和其他所有方框的IOU结果。
        ious = overlaps / (areas[i] + areas[index[1:]] - overlaps)
        print('ious is', ious)
        print(type(ious))

        # 接下来是合并重叠度最大的方框，也就是合并ious中值大于thresh的方框
        # 我们合并的操作就是把他们剔除，因为我们合并这些方框只保留下分数最高的。
        # 我们经过排序当前我们操作的方框就是分数最高的，所以我们剔除其他和当前重叠度最高的方框
        # 这里np.where(ious<=thresh)[0]是一个固定写法。
        idx = np.where(ious <= thresh)[0]
        print('idx:',idx)
        print(type(idx))

        # 把留下来框在进行NMS操作
        # 这边留下的框是去除当前操作的框，和当前操作的框重叠度大于thresh的框
        # 每一次都会先去除当前操作框，所以索引的列表就会向前移动移位，要还原就+1，向后移动一位
        index = index[idx + 1]  # because index start from 1
        print(index)
    return keep

keep = py_cpu_nms(boxes,0.7)
print(keep)