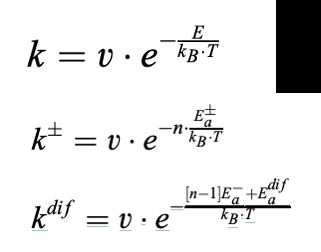我在CSDN开组会1-蒙特卡洛模拟在矿床学的应用展望
各位老师、同学们,大家好。今天组会的内容是蒙特卡洛模拟在矿床学的应用展望。
为什么要讲蒙特卡洛模拟呢,因为我发现在地质学方面已经有不少应用,但是蒙特卡洛模拟延伸的知识太晦涩了,劝退了很多探究者们。因此,计划开展一场专题报告,如有不足之处,请批评指正。
1 蒙特卡洛的介绍
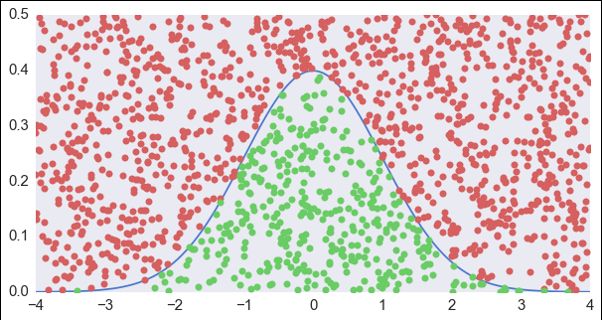
蒙特卡洛方法又称统计模拟法,是一种随机模拟方法,以概率和统计理论方法为基础的一种计算方法,是使用随机数(或更常见的伪随机数)来解决很多计算问题的⽅法。
将所求解的问题同一定的概率模型相联系,用电子计算机实现统计模拟或抽样,以获得问题的近似解。为象征性地表明这一方法的概率统计特征,故借用赌城蒙特卡洛命名。
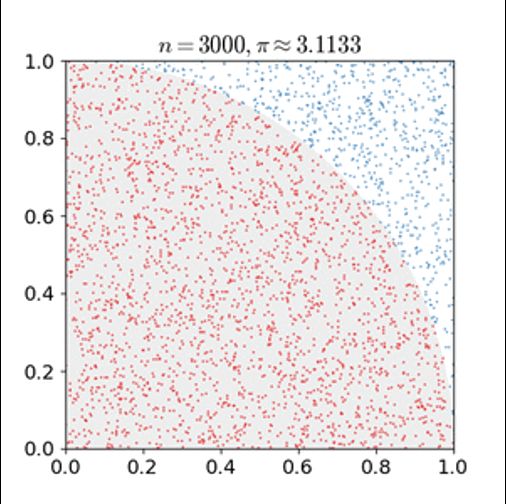
蒙特卡洛方法最早在原子弹的研制中正式提出,而事实上,1777年,法国Buffon提出用投针实验的方法求圆周率,这被认为是蒙特卡洛方法的起源。
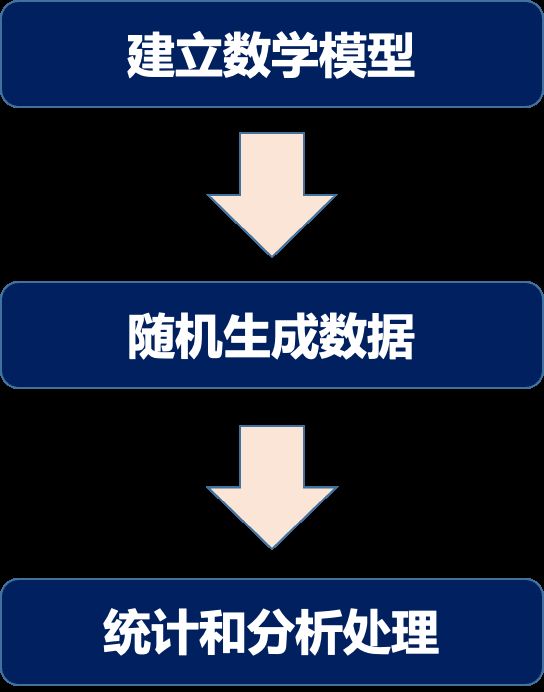
通常来讲,蒙特卡洛模拟应当包括是三个方面,第一是建立数学模型,然后随机生成数据,最后进行统计和分析处理。详细描述如下:
-
在蒙特卡洛模拟中,首先需要建立一个描述系统的数学模型,并明确所关注的属性或行为,例如材料的热力学性质、相变行为、输运性质等。
-
然后,通过随机生成大量的模拟数据,这些数据是基于系统模型和特定的概率分布。
-
最后,利用统计方法对这些数据进行分析和处理,从而得出关于系统的性质和行为的结果。
蒙特卡洛在众多领域都有所应用,例如材料学、物理科学、生命科学以及计算机科学、金融工程等。
2 蒙特卡洛模拟的地质学应用
尽管蒙特卡洛模拟应用众多,但是在地质学领域仍没有做到普及。在此列举主要的几个研究方向。
2.1 动力学蒙特卡洛模拟
文献1 The effect of crystal size variation on the rate of dissolution – A kinetic Monte Carlo study (Briese et al., 2017,GCA)
摘要:
晶体尺寸是许多地球化学过程的重要参数,并且经常被观察到对晶体溶解速率有显著影响。虽然尺寸与溶解度的关系通常用热力学术语(临界半径)来描述,但尺寸与溶解速率的机理基础并不详细。在这里,我们检验了尺寸对溶解速率的影响,以及这种关系与其他参数无关的机理。我们使用动力学蒙特卡罗模型方法观察了四个简单立方晶体(边缘尺寸d=25,64,125,187个晶胞)溶解过程中的原子变化。这些模拟保持了代表不饱和、远离平衡状态的恒定解边界条件。我们观察到表面积归一化溶解速率随着初始晶体尺寸的减小而非线性增加。这种关系可以从机理上理解,部分是扭结原子位和阶跃原子位形成的耦合。在这两个约束条件大致平衡的条件下,总溶解速率最大,质量去除最有效。这种关系反映了扭结原子和台阶原子形成的相互依赖性,它们的高分离频率对溶解过程起主导作用。
关键信息:
Fig. 1. Specific surface sites of a Kossel-type crystal that are characterized through their number of nearest neighbors or the number of bonds. Terrace atoms have 5 nearest neighbors, step atoms have 4, kink atoms have 3, and adatoms have only one.
针对晶体溶解速率的情况,需要先有公式:
where kB and T are Boltzmann’s constant and absolute temperature, respectively. E represents the activation energy necessary for a transition from one state to another, and m is the so-called frequency factor.
在阿伦尼乌兹方程公式中,k表示着速率,k-表示着溶解速率,k+表示着吸附速率。kdif表示着表面扩散情况。好了 到此为止,不必深究。作者主要计算的是k-,并将k+设置为了无穷小。
接着作者假设了四种尺寸的晶体,并让他们先附着上4000个原子。
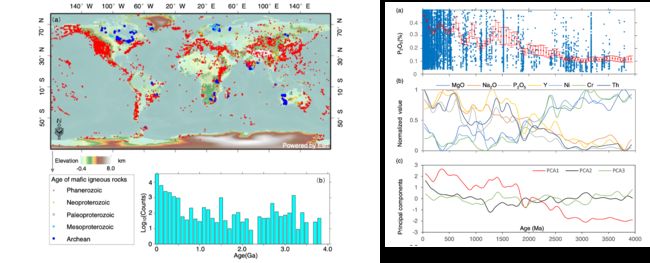
文献2 Reconstructing Earth’s atmospheric oxygenation history using machine learning*,Chen et al., NC,2023
在这里,我们提出了一个独立的策略——利用全球镁铁质火成岩地球化学大数据进行机器学习,以探索过去40亿年的大气情况。地球的含氧大气可能至少部分是地幔冷却的结果,特别是不断演变的地幔熔融过程帮助调节了早期地球大气的平衡。
作者首先手机了全球的镁铁质火成岩地球化学的数据,这个有对应的数据库,不是主要的问题。接着进行了主成分分析,因为元素很多所以进行降维,可以理解。
但是为什么和大气氧化事件联系起来了呢?因为作者发现镁铁质火成岩的数据分析结果和两期氧化事件能匹配上。所以有了后续的研究工作。
作者建立了质量变化的方程,其中重要的是ma质量方程。这个函数由SVR支持向量回归获得函数方程式。接着使用恶魔那个特卡了模拟得到结果。
文献3
Compositional and thermal state of the lower mantle from joint 3D inversion with seismic tomography and mineral elasticity
Deng et al., 2023,PANS
在本研究中,我们采用马尔可夫链蒙特卡罗框架,根据地震层析成像和矿物弹性数据反演了下地幔的 3D 化学成分和热状态。
文献4
Markov chain Monte Carlo inversion of mantle temperature and source composition, with application to Reykjanes Peninsula, Iceland
Brown et al., 2020, EPSL
为了克服这些局限性,我们提出了一种将马尔可夫 链蒙特卡罗(MCMC)采样方法与REEBOX PRO正向地幔融化模型相结合的逆方法。我们使用此工具来约束冰岛雷克雅尼斯半岛下方的地幔潜在温度,熔体体积以及地幔源岩性的微量元素和同位素组成。
在这里 就需要提到马尔科夫链蒙特卡洛模拟了。
1、构建马尔科夫链
1.1 马尔科夫链初始化
(1)从先验概率分布q(m)中随机得到一组输入参数m**(但m数据必须有效)**。
(2)设定迭代变量t,将当前参数写为m**t**。
(3)因此这个根据观察值进行的结果拟合量化为似然函数[L(d, mt)]**。**
1.2模型参数限定
(1)设定一个新的模型参数mt‘,是对mt参数扰动的结果。
1.3模型参数判定
(1)计算接受率。R=(ρ(m(t^′,d)))/(ρ(m(t^ ,d)))
(2)从均匀分布中取随机数r与R比较,当r≤R时,将mt‘添加到马尔科夫链中。t值+1,若反之,则t不变(保持当前状态)。
1.4迭代
(1)重复进行参数限定和判定,指导达到规定迭代次数。
3 蒙特卡洛模拟的研究展望
1. 建立符合矿床学事实的数值模型,运用蒙特卡洛模拟获取分布特征
2. 使用马尔科夫链蒙特卡洛模拟,反演数值模型的基本参数概率分布
3. 使用动力学蒙特卡洛模拟,确定研究材料的宏观失效
4蒙特卡洛模拟实操展示
-
1. 使用EXCEL*进行蒙特卡洛模拟
用鼠标选中A列,在编辑栏,输入Rand函数:
=RAND();并按【Ctrl+Enter】结束确认,即可生成一列随机小数;=ROUND(RAND(),2);让随机数,强制保留两位小数=RANDBETWEEN(最小整数,最大整数)生成服从正态分布的随机数Excel 函数格式
“=NORMINV(probability,mean,standard_dev)”参数解释:Probability - 正态分布的概率值,取值范围(0,1)Mean - 算术平均值;Standard_dev - 标准差。=NORMINV(RAND(),0,1)生成均值为0,标准差为1的正态分布随机数
-
2. 使用*Python进行蒙特卡洛模拟
-
random.random()random.random() 方法返回一个随机数,其在 0 至 1 的范围之内。以下是其具体用法:
import randomrandom.random()-
random.uniform()random.uniform(a , b) 是在指定范围内生成随机数,其有两个参数,一个是范围上限,一个是范围下限,顺序可交换
import randomrandom.uniform(2,6)-
random.randint()random.randint(a , b) 是随机生成指定范围内的整数,其有两个参数,一个是范围上限,一个是范围下限,顺序不可交换。
import randomrandom.randint(2,6) -
-
3. 使用*R*语言进行蒙特卡洛模拟
sample(x, size, replace, prob)x 表示从x中选取随机数,x可以是一个向量(可以由一个元素或者多个元素组成)。size表示随机生成的随机数的个数,是一个非负的整数。replace表示抽取方式(replace = TRUE 表示可放回抽取,replace = FLASE表示不可放回抽取)。prob表示按照给定的概率抽取,由一个向量组成(默认prob = NULL)set.seed()函数设置随机种子,如果设置了随机种子每次的随机数是相同的。目的是方便以后他人进行测试。runif()函数:随机生成均匀分布的小数runif(n, min = 0, max = 1)n表示随机生成小数的个数。min = 0,max = 1,表示小数的范围在0-1之间。
rnorm()函数:生成服从正态分布的随机数rnorm(n, mean = 0, sd = 1)生成长度为n的向量,向量中的每一个值服从正态分布。
| 函数 | 概率分布 |
|---|---|
| rexp | 指数分布 |
| rf | F分布 |
| rgamma | Gamma分布 |
| rgeom | 几何分布 |
| rhyper | 超几何分布 |
| rlogis | Logistic分布 |
| rmultinom | 多项式分布 |
| rpois | 泊松分布 |
| rt | t分布 |
| rchisq | 卡方分布 |