Leetcode力扣秋招刷题路-0081

从0开始的秋招刷题路，记录下所刷每道题的题解，帮助自己回顾总结

81. 搜索旋转排序数组 II

已知存在一个按非降序排列的整数数组 nums ，数组中的值不必互不相同。

在传递给函数之前，nums 在预先未知的某个下标 k（0 <= k < nums.length）上进行了 旋转 ，使数组变为 [nums[k], nums[k+1], …, nums[n-1], nums[0], nums[1], …, nums[k-1]]（下标 从 0 开始 计数）。例如， [0,1,2,4,4,4,5,6,6,7] 在下标 5 处经旋转后可能变为 [4,5,6,6,7,0,1,2,4,4] 。

给你 旋转后 的数组 nums 和一个整数 target ，请你编写一个函数来判断给定的目标值是否存在于数组中。如果 nums 中存在这个目标值 target ，则返回 true ，否则返回 false 。

你必须尽可能减少整个操作步骤。

示例 1：
输入：nums = [2,5,6,0,0,1,2], target = 0
输出：true

示例 2：
输入：nums = [2,5,6,0,0,1,2], target = 3
输出：false

提示：
1 <= nums.length <= 5000
$-10^4$ <= nums[i] <= $10^4$
题目数据保证 nums 在预先未知的某个下标上进行了旋转
$-10^4$ <= target <= $10^4$

方法一：
方法一是要找到旋转位置，非递减数组此前在下标k处（k=0时相当于未进行旋转）进行了旋转，当k≠0时，那么现在在下标M处【M=len-k-1】必定有nums[M]>=nums[M+1],当且仅当数组中每个元素相等时等号成立。
于是可以找这样的M,我们可以边顺序查找target,边找M；若这样未找到target，然后在M+1到数组末尾处采用二分查找。这样做最好情况下时间复杂度为O(logn),最坏情况下为O(n),平均O(n),k越小情况越坏;

public boolean search(int[] nums, int target) {
    int M=0;
    while(M=l){
        int mid=(l+r)/2;
        if(nums[mid]==target) return true;
        else if(nums[mid]

方法二：
方法二采用整体二分法的思想，我们用一张抽象的图来分析。

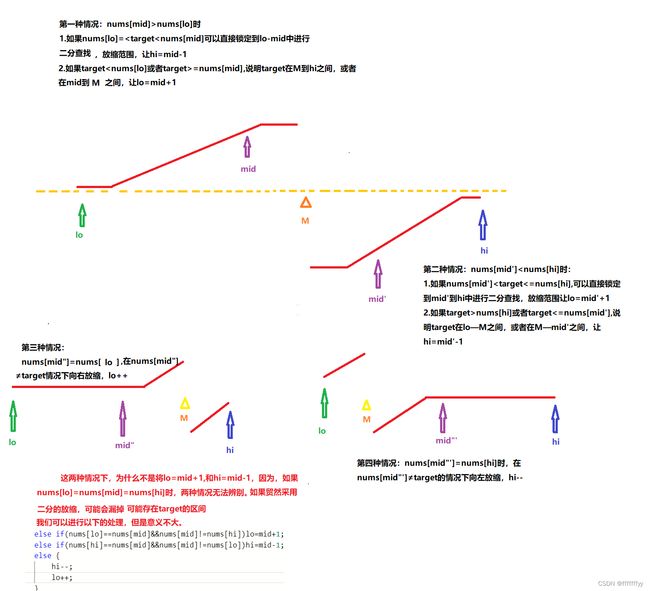
另外nums[mid]>nums[hi]的情况与nums[mid]>nums[lo]一致，nums[mid]

public boolean search(int[] nums, int target) {
    int lo=0,hi=nums.length-1;
    while(lo<=hi){
        int mid=(lo+hi)/2;
        if(nums[mid]==target) return true;
        if(nums[mid]=target&&nums[mid]nums[lo]){
            if(nums[lo]<=target&&nums[mid]>target) hi=mid-1;
            else lo=mid+1;
        }else if(nums[mid]==nums[lo]) lo++;
        else hi--;
    }
    return false;
}