滑动窗口4：LeetCode209. 长度最小的子数组

题目要求：给定一个含有 n 个正整数的数组和一个正整数 target 。

找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, ..., numsr-1, numsr] ，并返回其长度。如果不存在符合条件的子数组，返回 0 。

示例：
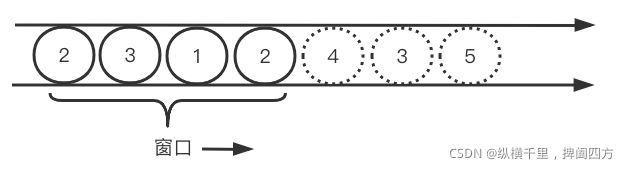
输入：target = 7, nums = [2,3,1,2,4,3]
输出：2
解释：子数组 [4,3] 是该条件下的长度最小的子数组。

1.暴力计算

这是一道经典的滑动窗口的问题。首先，我们留意这里说的是连续，如果忽略了这个条件，后面所有的讨论就没有意义了。

既然连续，那我们想到的第一种方法就是两次遍历找一下就行了。

枚举数组 nums 中的每个下标作为子数组的开始下标，对于每个开始下标 i，需要找到大于或等于 i的最小下标 j，使得从 nums[i] 到 nums[j] 的元素和大于或等于 s，并更新子数组的最小长度（此时子数组的长度是 j−i+1）。

我们声明一个变量ans来标记每次获得结果的长度，如果当前次的更小，我们就更新，否则就保留上一次的，假如没有就将ans标记为无穷大。

class Solution {
    public int minSubArrayLen(int s, int[] nums) {
        int n = nums.length;
        if (n == 0) {
            return 0;
        }
        int ans = Integer.MAX_VALUE;
        for (int i = 0; i < n; i++) {
            int sum = 0;
            for (int j = i; j < n; j++) {
                sum += nums[j];
                if (sum >= s) {
                    ans = Math.min(ans, j - i + 1);
                    break;
                }
            }
        }
        return ans == Integer.MAX_VALUE ? 0 : ans;
    }
}

很显然这种处理的效率不高，我们还是看一下如何使用滑动窗口来解决。

2.滑动窗口

思路其实非常简单，我们把数组中的元素不停的入队，直到总和大于等于 s 为止，接着记录下队列中元素的个数，然后再不停的出队，直到队列中元素的和小于 s 为止（如果不小于 s，也要记录下队列中元素的个数，这个个数其实就是不小于 s 的连续子数组长度，我们要记录最小的即可）。接着再把数组中的元素添加到队列中……重复上面的操作，直到这里以 [2,3,1,2,4,3] 举例画个图来看下数组中的元素全部使用完为止。

 因为是连续的，所以我们先让其入队直到达到大约等于s，此时我们就找到的第一个满足要去的长度len1。然后就开始出队，直到队列的结果小于s，这里是为了能放下一个元素。

 

 这里的窗口大小是变化的，但是窗口内的元素之和一定是在当前位置刚刚大于等于s。此时的队列大小就是我们需要的一个ans。

上面画的是使用队列，但在代码中我们不直接使用队列，我们使用两个指针，一个指向队头一个指向队尾，我们来看下代码：

    public int minSubArrayLen(int s, int[] nums) {
        int lo = 0, hi = 0, sum = 0, min = Integer.MAX_VALUE;
        while (hi < nums.length) {
            sum += nums[hi++];
            while (sum >= s) {
                min = Math.min(min, hi - lo);
                sum -= nums[lo++];
            }
        }
        return min == Integer.MAX_VALUE ? 0 : min;
    }

 你也许会注意到，我们这里也是两层循环，为什么效率就比上面的暴力方式高呢？这是因为内层的while循环每次处理的元素是非常少的，不是整个数组的长度，因此会快很多。我们缩小查找范围，但不一定是非要去掉循环。

3.双指针优化

除了滑动窗口，本题还可以使用二分的方式来优化，二分也是避免循环时需要O(n)查整个数组。

我们可以申请一个临时数组 sums，其中 sums[i] 表示的是原数组 nums 前 i 个元素的和，题中说了 “给定一个含有 n 个 正整数 的数组”，既然是正整数，那么相加的和会越来越大，也就是sums数组中的元素是递增的。我们只需要找到 sums[k]-sums[j]>=s，那么 k-j 就是满足的连续子数组，但不一定是最小的，所以我们要继续找，直到找到最小的为止。怎么找呢，我们可以使用两个 for 循环来枚举，但这又和第一种暴力求解一样了，所以我们可以换种思路，求 sums[k]-sums[j]>=s 我们可以求 sums[j]+s<=sums[k]，那这样就好办了，因为数组sums中的元素是递增的，也就是排序的，我们只需要求出 sum[j]+s 的值，然后使用二分法查找即可找到这个 k。

    public int minSubArrayLen(int s, int[] nums) {
        int length = nums.length;
        int min = Integer.MAX_VALUE;
        int[] sums = new int[length + 1];
        for (int i = 1; i <= length; i++) {
            sums[i] = sums[i - 1] + nums[i - 1];
        }
        for (int i = 0; i <= length; i++) {
            int target = s + sums[i];
            int index = Arrays.binarySearch(sums, target);
            if (index < 0)
                index = ~index;
            if (index <= length) {
                min = Math.min(min, index - i);
            }
        }
        return min == Integer.MAX_VALUE ? 0 : min;
    }

注意这里的函数 int index = Arrays.binarySearch(sums, target);如果找到就会返回值的下标，如果没找到就会返回一个负数，这个负数取反之后就是查找的值应该在数组中的位置
举个例子，比如排序数组 [2，5，7，10，15，18，20] 如果我们查找 18，因为有这个数会返回 18 的下标 5，如果我们查找 9，因为没这个数会返回 -4（至于这个是怎么得到的，大家可以看下源码，这里不再过多展开讨论），我们对他取反之后就是3，也就是说如果我们在数组中添加一个 9，他在数组的下标是 3，也就是第 4 个位置（也可以这么理解，只要取反之后不是数组的长度，那么他就是原数组中第一个比他大的值的下标）。

 在基础算法中很多人会关心什么时候需要自己写binarySearch，什么时候可以使用库函数。其实关键点在于这个问题的关键是否是二分查找，这里的只是我们解决一个更复杂问题的一个步骤，那么这时候就可以使用的。