Pixel Adaptive Deep Unfolding Transformer for Hyperspectral Image Reconstruction

代码地址

1. 摘要

Hyperspectral Image (HSI) reconstruction has made gratifying progress with the deep unfolding framework by formulating the problem into a data module and a prior module. Nevertheless, existing methods still face the problem of insufficient matching with HSI data. The issues lie in three aspects: 1) fixed gradient descent step in the data module while the degradation of HSI is agnostic in the pixel-level. 2) inadequate prior module for 3D HSI cube. 3) stage interaction ignoring the differences in features at different stages. To address these issues, in this work, we propose a Pixel Adaptive Deep Unfolding Transformer (PADUT) for HSI reconstruction. In the data module, a pixel adaptive descent step is employed to focus on pixel-level agnostic degradation. In the prior module, we introduce the Non-local Spectral Transformer (NST) to emphasize the 3D characteristics ofHSI for recovering. Moreover, inspired by the diverse expression of features in different stages and depths, the stage interaction is improved by the Fast Fourier Transform (FFT). Experimental results on both simulated and real scenes exhibit the superior performance of our method compared to state-of-theart HSI reconstruction methods.

高光谱图像（HSI）重建在深度学习框架上通过将问题分解为数据模块和先验模块取得了令人满意的进展。然而，现有的方法仍然面临着与 HSI 数据匹配不足的问题。问题主要体现在三个方面：1）在数据模块中固定梯度下降步长，而 HSI 的下降在像素级是不可知的。2）HSI 三维立方体的先验模块不足。3）阶段交互忽略了不同阶段特征的差异。为了解决这些问题，在本工作中，我们提出一种像素自适应深度展开 Transformer（PADUT）。在数据模块中，采用像素自适应下降步长（pixel adaptive descent step）来关注像素级的不可知退化（pixel-level agnostic degradation）。在先验模块中，我们引入了非局部光谱 Transormer（NST）来强调 HSI 的三维特征来进行恢复。此外，受不同阶段和深度特征的多样化表达的启发，采用快速傅里叶变换（FFT）改进了阶段交互。仿真和真实场景的实验结果表明，该方法与目前最先进的 HSI 重建方法相比具有更好的性能。

2. 目的

根据学习策略的不同，基于深度学习的方法大致可以分为端到端学习方法和模型辅助方法两大类。端到端学习方法通过蛮力映射恢复原始HSI，学习空间和光谱信息。没有物理模型的指导，这些端到端学习方法是黑盒，缺乏透明度。模型辅助方法利用了 HSI 退化到深度网络的物理特性，从而获得了固有的可解释性。

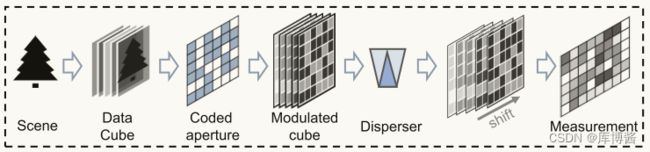
图1：编码孔径快照光谱成像（CASSI）系统。编码测量中的不同位置可能遭受不同程度的退化。

深度展开框架将神经网络的迭代优化算法展开，通常包括一个数据模块和一个先验模块。如图2所示，在测量过程中，三维立方体中不同位置的像素被不可知地压缩，而现有算法在数据模块中忽略了这种像素特异性的退化。对于先验模块，降噪在多阶段优化中起着至关重要的作用。由于 HSIs 是三维表示，现有的去噪器如何有效地利用空间-光谱信息仍然是一个问题。此外，在迭代恢复过程中，为了在获得综合特征的同时防止关键信息的丢失，需要进行跨阶段融合。我们观察到频率信息在不同的阶段和深度变化，见图3。前一编码器层的特征具有更清晰的振幅信息（amplitude），前一编码器层的特征具有更清晰的相位（phase）信息。

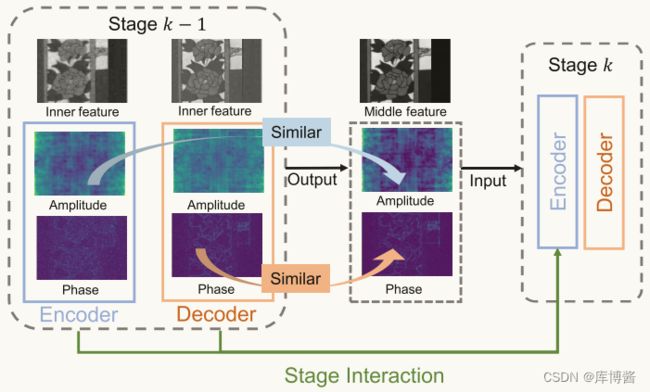
图2：深度展开网络的内在特征在频域的可视化。振幅/相位图像由内部特征提取，相位/振幅分量设为常数。

3. 网络设计

3.1 Problem Formulation

基于压缩理论，CASSI 系统可以捕获包含所有波段信息的压缩信息。图1说明了编码过程的基本流程。考虑一张以 $\lambda$ 为波长的光谱图片 $X_{\lambda }\in {\mathbb{R}}^{M\times N}$，从真实场景中获取到的 HSI 首先通过一个编码孔径 $C_{\lambda }\in {\mathbb{R}}^{M\times N}$ 进行调制。The temporary measurement 表示为：
$$Y_{\lambda }=C_{\lambda }\odot X_{\lambda }$$
其中 $\odot$ 表示 element-wise multiplication。根据色散函数（dispersive function）$d$ 将 $Y_{\lambda }$ 沿着水平方向移动，将 intermediate measurement $Y_{\lambda }^{\prime }\in {\mathbb{R}}^{M\times (N+B-1)}$ 调制为：
$$Y_{\lambda }^{\prime }(h,w)=G_{\lambda }^{\prime }(h,w+d(\lambda ))$$
其中 $h$ 和 $w$ 表示空间坐标。$B$ 是所需的 3D HSI 的光谱数。在存在噪声 $N_{\lambda }\in {\mathbb{R}}^{M\times (N+B-1)\times B}$ 的情况下，final measurement $Y\in {\mathbb{R}}^{M\times (N+B-1)\times B}$ 为：
$$Y=\sum _{\lambda =1}^B{G}_{\lambda }^{\prime }+N$$

CASSI 系统通过牺牲空间信息来获取光谱信息。因此，编码测量 $y$ 中的空间强度包含了空间和光谱信息的组合表示。这表明在 HSI 中不同位置的像素可能有不同的压缩水平。这促使我们在优化过程中对 pixel-specific reconstruction 进行改进。

3.2 Revisting the Deep Unrolling Framework

在数学上，HSI 重构的优化过程可建模为：
$$\hat{x}=arg\underset{x}{\min }\frac{1}{2}{||y-\Phi x|{|}_2}^2+\eta J(x)$$
其中 $J(x)$ 表示参数 $\eta$ 的正则项。The coding mask $\Phi$ reveals the spatial relation as well as the spectral relation between the coded measurement and desired 3D data. 在 half quadratic splitting（HQS）算法中，通过引入辅助变量 $z$ 将上式表示为子问题：
$$(\hat{x},\hat{z})=arg\underset{x,z}{\min }\frac{1}{2}{||y-\Phi x|{|}_2}^2+\eta J(z)+\frac{\mu }{2}{||z-x|{|}_2}^2$$
其中，$\mu$ 为惩罚参数。HQS 算法通过两个迭代收敛子问题近似优化上式：
$$\begin{array}{c}{x}^{k+1}=arg{\min }_x{||y-\Phi x^k|{|}_2}^2+\mu {||z^k-x^k|{|}_2}^2\\ \\ z^{k+1}=arg{\min }_z\frac{\mu }{2}{||z^k-x^{k+1}|{|}_2}^2+\eta J(z^k)\end{array}$$
简而言之，$x$ 的近似解为：
$$\begin{array}{cc}{x}^{k+1}& =({\Phi }^T\Phi +\mu I{)}^{-1}(\Phi y+\mu z^k)\\ & =z^k+\frac{1}{1+\mu }{\Phi }^T(\Phi {\Phi }^T{)}^{-1}(y-\Phi z^k)\end{array}$$
在深度展开方法中，$z$ 的解通常为：
$$z^{k+1}=P_{k+1}(x^{k+1})$$
其中 $P_{k+1}$ 为 $k+1$ 阶段的深度网络。通常，深度展开框架由多个阶段组成，这些阶段是专门为从编码测量 $y$ 重建底层 HSI 立方体 $x$ 而设计的。

3.3 Framework

图3：我们提出的用于 HSI 重建的像素自适应深度展开 Transformer（PADUT）的插图。Top：由 k 个阶段组成的整体架构，每个阶段由一个数据模块和一个先验模块组成。

基于上述讨论结果，我们设计了一种像素自适应深展开 Transformer。在每个阶段，一个数据模块之后是一个降噪器，降噪器指的是先验模块。数据模块的目的是利用物理退化信息，而先验模块的目的是优化。我们的降噪器是 u 型网络设计。在编码器中，每一层包含一个 Fast Fourier Transformer stage fusion（FFT-SF）层和一个 Non-local Spectral Transformer（NST）层。解码器仅由 NST 层组成。

3.3.1 Pixel-Adaptive Prior Module

观察之前的式子，我们发现 $\frac{1}{1+\mu }$ 对于优化 $x$ 起着非常关键的作用。为了简化说明，我们用 $F_{\sigma }$ 表示 $\frac{1}{1+\mu }$：
$$x^{k+1}=z^k+F_{\sigma }{\Phi }^T(\Phi {\Phi }^T{)}^{-1}(y-\Phi z^k)$$
在压缩感知过程中，由于 modulation 的原因，不同位置和不同波段的图像有明显的不同。由于 instrument noise 的存在，噪声在 HSI 立方体中的分布也发生了变化。这种差异在整个恢复过程中都存在。针对 HSI 在不同位置出现的不一致和不可知的退化问题，我们设计了一个 Pixel-Adaptive Prior Module 来实现深度展开框架。

由于物理掩模 $\Phi$ 建立了空间维数和光谱维数的相关性，而 $z^k$ 表示当前输入特征，我们通过卷积层和 Channel Attention（CA）层生成 3D 参数 $F_{\sigma }$：
$$\begin{array}{c}{F}_{\sigma }^{\prime }=Conv(Concat[z^k,\Phi ])\\ F_{\sigma }=CA(F_{\sigma }^{\prime })\end{array}$$
然后，将得到的 3D 参数 $F_{\sigma }$ 通过像素自适应梯度下降 pixel-adaptive gradient descent step 步对 3D 数据进行参数化，实现像素化重建。

3.3.2 Non-local Spectral Transformer

光谱自注意力机制在图像恢复领域显示出良好的效果。然而，它很难在空间和光谱维度上模拟像素之间的细粒度相似性特征。一方面，由于光谱自注意力机制以整个光谱维的像素作为特征值来表征光谱特征，局部细节信息容易丢失。另一方面，由于 CASSI 系统的编码特性，压缩后的信息往往会出现在相邻区域。光谱自注意力机制需要更好地适应三维 HSI 立方体和编码系统。为了利用 HSI 的空间光谱信息，我们在先验模块中提出了用于 HSI 恢复的非局部光谱Transformer（Non-local Spectral Transformer, NST）。在两个 NST 之间进行空间移位运算，以探索更多的局部特征。

对于非局部光谱注意力机制层，我们首先将 $x_{in}\in {\mathbb{R}}^{H\times W\times C}$ 的整个特征分割为若干个立方体 patch，分别为 $x_1,x_2,...,x_G$。每个立方体的大小为 $L\times L\times C$。得到的每个空间光谱立方体的注意力图大小为 ${\mathbb{R}}^{C\times C}$，捕获并整合整个数据体的非局部信息。

3.3.3 Fast Fourier Transform Stage Fusion

深度展开框架表明了通过可解释网络进行多阶段学习的有效性。由于上下文信息和细节信息在不同的阶段是不同的，有效地利用丰富的特征可以提高重构性能。此外，在每个阶段，由于空间信息和光谱信息之间的内在平衡，编码器-解码器降噪会导致上下文不同的中间特征。如何更有效地插入跨阶段特征和内部阶段特征仍然是一个持续的挑战。

如图2所示，在频域中，重建的 HSI 在不同阶段的相位分量和振幅分量对应不同。在编码器中，数量级信息更为突出。在后一种解码器中，相位信息更加清晰。根据这一观察，我们在级间连接中引入快速傅里叶变换 Fast Fourier Transform，从频域得到较好的重构结果。

我们的FFT-SF的细节如图3 © 所示。我们首先将前一层的编码器和解码器特征变换到傅里叶域。然后，针对不同的频率特性进行基于傅立叶变换的融合。最后，利用频率增强特征 frequency-enhanced feature 增强下一阶段的特征。为了将 $x$ 的频率特征建模为 ${\mathbb{R}}^{H\times W\times C}$ 的形状，我们利用傅里叶变换 $\mathcal{F}$ 将其转化为傅里叶域，其表达式为 $\mathcal{F}(x)$：
$$\begin{array}{cc}\mathcal{F}(x)& =x(\mu ,\vartheta )\\ & =\frac{1}{\sqrt{HW}}{\sum }_{h=0}^{H-1}{\sum }_{w=0}^{W-1}x(h,w)e^{-j2\pi (\frac{h}{H}\mu +\frac{w}{W}\vartheta )}\end{array}$$
其中 $\mu$ 和 $\vartheta$ 表示频域坐标。为了分析和利用 HSIs 的频率特性，我们将复分量 $x(\mu ,\vartheta )$ 分解为振幅 $A(x)$ 和相位 $P(x)$。幅值分量提供了对像素强度的洞察力，而相位分量对于传递位置信息至关重要。 其数学公式为：
$$\begin{array}{c}A(x(\mu ,\vartheta )=\sqrt{R^2(x(\mu ,\vartheta ))+I^2(x(\mu ,\vartheta ))}\\ \\ P(x(\mu ,\vartheta ))=arctan[\frac{I(x(\mu ,\vartheta ))}{R(x(\mu ,\vartheta ))}]\end{array}$$
其中 $R(x)$ 和 $I(x)$ 表示实部和虚部。

对于第 $(k+1)$ 阶段，前一阶段的特征表示为 $F_{enc}^k$ 和 $F_{dec}^k$，当前编码器层的特征表示为 $F_{enc}^{k+1}$。根据在编码器和解码器中观察到的幅值信息和相位信息，FFT 阶段融合表示为：
$$\begin{array}{c}{F}_s^{k+1^{\prime }}={\mathcal{F}}^{-1}(A(F_{enc}^k),P(F_{dec}^k))\\ \\ F_s^{k+1}=Conv(Concat(F_s^{k+1^{\prime }},F_{enc}^{k+1}))\end{array}$$
${\mathcal{F}}^{-1}$ 表示傅里叶反变换。