matlab层次分析法模型及相关语言基础

发现更多计算机知识，欢迎访问Cr不是铬的个人网站

代码放在最后面!

这篇文章是学习层次分析法模型的笔记。

1.什么时候用层次分析法

层次分析法是建模比赛中最基础的模型之一，其主要用于解决评价类问题（例如：选择哪种方案最好、哪位运动员或者员工表现的更优秀）。

层次分析法式利用各项指标的不同权重来进行判断的模型。就比如这样的：

---

2.关于权重表

关于上图的表作进一步的说明。这个表的评分是根据数据来的，但是每天每次这种数据可能略有不同，那么计算的得分不也就不同了吗？为了消除这种差异，我们引进的是相对的概念！

根据这个表格的规则来填写，就变得更加的稳定且准确。

3.一致矩阵

刚刚我们根据那个规则填写出来的表是判断矩阵。那么什么是一致性矩阵呢？

满足如图的公式的矩阵我们称之为一致性矩阵！

---

其实也就是各行各列成倍数关系

4.一致性检验

一致性检验就是检验我们构造的判断矩阵和一致性矩阵的差别大不大。

一致性矩阵的充要条件:

一致性检验步骤

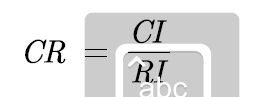
计算一致性指标

---

查找平均随机一致性指标

---

计算一致性比例CR

如果CR < 0.1,那么代表其能够通过一致性检验！

一致性矩阵如何计算权重

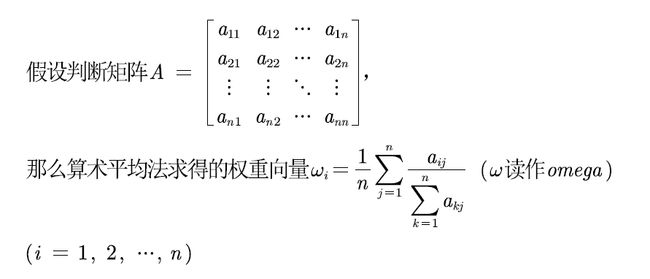
在判断为一致性矩阵后，我们来计算权重值。有这么三种方法:算术平均法

算术平均法求权重

• 将判断矩阵归一化

• 将归一化的矩阵按行求和

• 将相加后得到的向量中每个元素除以n即可得到权重向量

几何平均法求权重

• 第一步：将A的元素按照行相乘得到一个新的列向量
• 第二步：将新的向量的每个分量开n次方
• 第三步：对该列向量进行归一化即可得到权重向量

---

特征值法

特征值法是最常用也是最重要的!

一致矩阵有一个特征值为n，其余特征值均为0

• 第一步：求出矩阵A的最大特征值以及其对应的特征向量
• 第二步：对求出的特征向量进行归一化即可得到我们的权重

层次分析法步骤

• 分析系统中各因素之间的关系，建立系统的递阶层次结构.

---

• 对于同一层次的各元素关于上一层次中某一准则的重要性进行两两比较，构造两两比较矩阵（判断矩阵）

---

• 由判断矩阵计算被比较元素对于该准则的相对权重，并进行一致性检验（检验通过权重才能用）.

在比赛中三种方法最好都用上。考虑健壮性

代码部分

Matlab基本的小常识

% (1)在每一行的语句后面加上分号(一定要是英文的哦;中文的长这个样子；)表示不显示运行结果

a = 3;

a = 5

% (2)多行注释:选中要注释的若干语句,快捷键Ctrl+R

% a = 3;

% a = 5

% (3)取消注释:选中要取消注释的语句,快捷键Ctrl+T

% 我想要取消注释下面这行

% 还有这一行

% clear可以清楚工作区的所有变量

clear

% clc可以清除命令行窗口中的所有文本,让屏幕变得干净

clc

% 所以大家在很多代码开头，都会见到:

clear;clc   % 分号也用于区分行。

% 这两条一起使用，起到“初始化”的作用，防止之前的结果对新脚本文件（后缀名是 .m）产生干扰。

输出和输入函数(disp 和 input)

% disp函数

% matlab中disp()就是屏幕输出函数，类似于c语言中的printf（）函数

disp('hello,math')

a = [1,2,3]    %同一行中间用逗号分隔，也可以不用逗号，直接用空格

a = [1 2 3]

disp(a) 

% 注意，disp函数比较特殊，这里可要分号，可不要分号哦

disp(a);

% matlab中两个字符串的合并有两种方法

% （1）strcat(str1,str2……,strn) 

 strcat('字符串1','字符串2') 

% （2）[str 1,str 2，……, str n]或[str1  str2  ……  strn]

['字符串1'  '字符串2']

['字符串1','字符串2']

% 一个有用的字符串函数：num2str  将数字转换为字符串

c = 100

num2str(c)

disp(['c的取值为' num2str(c)])

disp(strcat('c的取值为', num2str(c)))

% input函数

% 一般我们会将输入的数、向量、矩阵、字符串等赋给一个变量，这里我们赋给A

A = input('请输入A：');

B = input('请输入B：')

% 注意观察工作区，并体会input后面加分号和不加分号的区别

sum函数

% （1）如果是向量（无论是行向量还是列向量），都是直接求和

E = [1,2,3]

sum(E)

E = [1;2;3]

sum(E)

% （2）如果是矩阵，则需要根据行和列的方向作区分

clc

E = [1,2;3,4;5,6]

% a=sum(x); %按列求和(得到一个行向量）

a = sum(E)

a = sum(E,1)

% a=sum(x,2); %按行求和(得到一个列向量）

a = sum(E,2)

% a=sum(x(:));%对整个矩阵求和

a = sum(sum(E))

a = sum(E(:))

基础：matlab中如何提取矩阵中指定位置的元素？

% （1）取指定行和列的一个元素（输出的是一个值）

clc;A=[1 1 4 1/3 3;1 1 4 1/3 3;1/4 1/4 1 1/3 1/2;3 3 3 1 3;1/3 1/3 2 1/3 1];

A

A(2,1)

A(3,2)

% （2）取指定的某一行的全部元素（输出的是一个行向量）

clc;A

A(2,:)

A(5,:)

% （3）取指定的某一列的全部元素（输出的是一个列向量）

clc;A

A(:,1)

A(:,3)

% （4）取指定的某些行的全部元素（输出的是一个矩阵）

clc;A

A([2,5],:)      % 只取第二行和第五行（一共2行）

A(2:5,:)        % 取第二行到第五行（一共4行）

A(2:2:5,:)     % 取第二行和第四行 （从2开始，每次递增2个单位，到5结束）

1:3:10

10:-1:1

A(2:end,:)      % 取第二行到最后一行

A(2:end-1,:)    % 取第二行到倒数第二行

% （5）取全部元素(按列拼接的，最终输出的是一个列向量)

clc;A

A(:)

size函数

A = [1,2,3;4,5,6]
B = [1,2,3,4,5,6]
size(A)
size(B)
% size(A)函数是用来求矩阵A的大小的,它返回一个行向量，第一个元素是矩阵的行数，第二个元素是矩阵的列数
[r,c] = size(A)
% 将矩阵A的行数返回到第一个变量r，将矩阵的列数返回到第二个变量c
r = size(A,1)  %返回行数
c = size(A,2) %返回列数

repmat函数

% B = repmat(A,m,n):将矩阵A复制m×n块，即把A作为B的元素，B由m×n个A平铺而成。
A = [1,2,3;4,5,6]
B = repmat(A,2,1)
B = repmat(A,3,2)

矩阵的运算

% MATLAB在矩阵的运算中，“*”号和“/”号代表矩阵之间的乘法与除法(A/B = A*inv(B))
A = [1,2;3,4]
B = [1,0;1,1]
A * B
inv(B)  % 求B的逆矩阵
B * inv(B)
A * inv(B)
A / B

% 两个形状相同的矩阵对应元素之间的乘除法需要使用“.*”和“./”
A = [1,2;3,4]
B = [1,0;1,1]
A .* B
A ./ B

% 每个元素同时和常数相乘或相除操作都可以使用
A = [1,2;3,4]
A * 2
A .* 2
A / 2 
A ./ 2

% 每个元素同时乘方时只能用 .^
A = [1,2;3,4]
A .^ 2
A ^ 2 
A * A

Matlab中求特征值和特征向量

% 在Matlab中，计算矩阵A的特征值和特征向量的函数是eig(A),其中最常用的两个用法：

A = [1 2 3 ;2 2 1;2 0 3]

% （1）E=eig(A)：求矩阵A的全部特征值，构成向量E。

E=eig(A)

% （2）[V,D]=eig(A)：求矩阵A的全部特征值，构成对角阵D，并求A的特征向量构成V的列向量。（V的每一列都是D中与之相同列的特征值的特征向量）

[V,D]=eig(A)

find函数的基本用法

% 下面例子来自博客：https://www.cnblogs.com/anzhiwu815/p/5907033.html 博客内有更加深入的探究

% find函数，它可以用来返回向量或者矩阵中不为0的元素的位置索引。

clc;X = [1 0 4 -3 0 0 0 8 6]

ind = find(X)

% 其有多种用法，比如返回前2个不为0的元素的位置：

ind = find(X,2)

%上面针对的是向量（一维），若X是一个矩阵（二维，有行和列），索引该如何返回呢？

clc;X = [1 -3 0;0 0 8;4 0 6]

ind = find(X)

% 这是因为在Matlab在存储矩阵时，是一列一列存储的，我们可以做一下验证：

X(4)

% 假如你需要按照行列的信息输出该怎么办呢？

[r,c] = find(X)

[r,c] = find(X,1) %只找第一个非0元素

矩阵与常数的大小判断运算

% 共有三种运算符：大于> ;小于< ;等于 ==  （一个等号表示赋值；两个等号表示判断）

clc

X = [1 -3 0;0 0 8;4 0 6]

X > 0

X == 4

判断语句

% Matlab的判断语句，if所在的行不需要冒号，语句的最后一定要以end结尾 ；中间的语句要注意缩进。

a = input('请输入考试分数:')

if a >= 85  

​    disp('成绩优秀')

elseif a >= 60 

​    disp('成绩合格')

else

​    disp('成绩挂科')

end

层次分析法代码

% 在开始下面正式的步骤之前，我们有必要检验下A是否因为粗心而输入有误
ERROR = 0;  % 默认输入是没有错误的
%(1)检查矩阵A的维数是否不大于1或不是方阵
[r,c]=size(A);
%size(A)函数是用来求矩阵的大小的,返回一个行向量，第一个元素是矩阵的行数，第二个元素是矩阵的列数
%[r,c]=size(A)  %将矩阵A的行数返回到第一个输出变量r，将矩阵的列数返回到第二个输出变量c

if r ~= c  || r <= 1
    % 注意哦，不等号是 ~=  (~是键盘Tab上面那个键，要和Shift键同时按才会出来)，别和C语言里面的!=搞混了
    % ||表示逻辑运算符‘或’（在键盘Enter上面，也要和Shift键一起按） 逻辑运算符且是 && （&读and，连接符号，是and的缩写。 ）
    ERROR = 1;
end
% Matlab的判断语句，if所在的行不需要冒号，语句的最后一定要以end结尾 ；中间的语句要注意缩进。

%(2)检验是否为正互反矩阵  a_ij > 0 且 a_ij * a_ji = 1
if ERROR == 0
    [n,n] = size(A);
    % 因为我们的判断矩阵A是一个非零方阵，所以这里的r和c相同，我们可以就用同一个字母n表示
    % 判断是否有元素小于0
    %    for i = 1:n
    %        for j = 1:n
    %            if A(i,j)<=0
    %                ERROR = 2;
    %            end
    %        end
    %    end
    if sum(sum(A <= 0)) > 0
        ERROR = 2;
    end
end

%顺便检验n是否超过了15，因为RI向量为15维
if ERROR == 0
    if n > 15
        ERROR = 3;
    end
end

if ERROR == 0
    % 判断  a_ij * a_ji = 1 是否成立
    if sum(sum(A' .* A ~=  ones(n))) > 0
        ERROR = 4;
    end
    % A' 表示求出 A 的转置矩阵，即将a_ij和a_ji互换位置
    % ones(n)函数生成一个n*n的全为1的方阵, zeros(n)函数生成一个n*n的全为0的方阵
    % ones(m,n)函数生成一个m*n的全为1的矩阵
    % MATLAB在矩阵的运算中，“/”号和“*”号代表矩阵之间的乘法与除法，对应元素之间的乘除法需要使用“./”和“.*”
    % 如果a_ij * a_ji = 1 满足， 那么A和A'对应元素相乘应该为1
end



if ERROR == 0
    % % % % % % % % % % % % %方法1： 算术平均法求权重% % % % % % % % % % % % %
    Sum_A = sum(A);
    SUM_A = repmat(Sum_A,n,1);
    Stand_A = A ./ SUM_A;
    disp('算术平均法求权重的结果为：');
    disp(sum(Stand_A,2)./n)
    % % % % % % % % % % % % %方法2： 几何平均法求权重% % % % % % % % % % % % %
    Prduct_A = prod(A,2);
    Prduct_n_A = Prduct_A .^ (1/n);
    disp('几何平均法求权重的结果为：');
    disp(Prduct_n_A ./ sum(Prduct_n_A))
    % % % % % % % % % % % % %方法3： 特征值法求权重% % % % % % % % % % % % %
    [V,D] = eig(A);
    Max_eig = max(max(D));
    [r,c]=find(D == Max_eig , 1);
    disp('特征值法求权重的结果为：');
    disp( V(:,c) ./ sum(V(:,c)) )
    % % % % % % % % % % % % %下面是计算一致性比例CR的环节% % % % % % % % % % % % %
    CI = (Max_eig - n) / (n-1);
    RI=[0 0.00001 0.52 0.89 1.12 1.26 1.36 1.41 1.46 1.49 1.52 1.54 1.56 1.58 1.59];  %注意哦，这里的RI最多支持 n = 15
    % 这里n=2时，一定是一致矩阵，所以CI = 0，我们为了避免分母为0，将这里的第二个元素改为了很接近0的正数
    CR=CI/RI(n);
    disp('一致性指标CI=');disp(CI);
    disp('一致性比例CR=');disp(CR);
    if CR<0.10
        disp('因为CR<0.10，所以该判断矩阵A的一致性可以接受!');
    else
        disp('注意：CR >= 0.10，因此该判断矩阵A需要进行修改!');
    end
elseif ERROR == 1
    disp('请检查矩阵A的维数是否不大于1或不是方阵')
elseif ERROR == 2
    disp('请检查矩阵A中有元素小于等于0')
elseif ERROR == 3
    disp('A的维数n超过了15，请减少准则层的数量')
elseif ERROR == 4
    disp('请检查矩阵A中存在i、j不满足A_ij * A_ji = 1')
end

本文由博客一文多发平台 OpenWrite 发布！