leetcode刷题 (数组——双指针)
双指针
双指针法(快慢指针法): 通过一个快指针和慢指针在一个for循环下完成两个for循环的工作。
双指针法(快慢指针法)在数组和链表的操作中是非常常见的,很多考察数组、链表、字符串等操作的面试题,都使用双指针法。
- 移除元素
给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素,并返回移除后数组的新长度。
不要使用额外的数组空间,你必须仅使用 O(1) 额外空间并 原地 修改输入数组。
元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。
示例 1:
输入:nums = [3,2,2,3], val = 3 输出:2, nums = [2,2]
解释:函数应该返回新的长度 2, 并且nums 中的前两个元素均为 2。你不需要考虑数组中超出新长度后面的元素。例如,函数返回的新长度为 2 ,而 nums = [2,2,3,3] 或 nums = [2,2,0,0],也会被视作正确答案。
示例 2:
输入:nums = [0,1,2,2,3,0,4,2], val = 2 输出:5, nums = [0,1,4,0,3]
解释:函数应该返回新的长度 5, 并且 nums 中的前五个元素为 0, 1, 3, 0,
4。注意这五个元素可为任意顺序。你不需要考虑数组中超出新长度后面的元素。
# python
# 双指针法(快慢指针法)在数组和链表的操作中是非常常见的,
# 很多考察数组、链表、字符串等操作的面试题,都使用双指针法。
class Solution:
def removeElement(self, nums: List[int], val: int) -> int:
slow = fast = 0
n = len(nums)
while(fast < n):
if nums[fast] != val:
nums[slow] = nums[fast]
slow += 1
fast += 1
return slow
# java
class Solution {
public int removeElement(int[] nums, int val) {
int slow = 0;
for(int fast = 0; fast < nums.length; fast++){
if(nums[fast] != val){
nums[slow] = nums[fast];
slow++;
}
}
return slow;
}
}
- 删除有序数组中的重复项
给你一个有序数组 nums ,请你 原地 删除重复出现的元素,使每个元素 只出现一次 ,返回删除后数组的新长度。
不要使用额外的数组空间,你必须在 原地 修改输入数组 并在使用 O(1) 额外空间的条件下完成。
示例 1:
输入:nums = [1,1,2] 输出:2, nums = [1,2]
解释:函数应该返回新的长度 2 ,并且原数组 nums的前两个元素被修改为 1, 2 。不需要考虑数组中超出新长度后面的元素。
示例 2:
输入:nums = [0,0,1,1,1,2,2,3,3,4] 输出:5, nums = [0,1,2,3,4]
解释:函数应该返回新的长度5 , 并且原数组 nums 的前五个元素被修改为 0, 1, 2, 3, 4 。不需要考虑数组中超出新长度后面的元素。
# python
class Solution:
def removeDuplicates(self, nums: List[int]) -> int:
slow = fast = 0
n = len(nums)
while(fast < n-1):
if nums[fast] != nums[fast+1]:
nums[slow+1] = nums[fast+1] # slow = 0 的数据一定是不重复的,所以直接 ++slow
slow += 1
fast += 1
return slow+1
# Java
class Solution {
public int removeDuplicates(int[] nums) {
int slow = 0;
int fast = 0;
while(fast < nums.length - 1){
if(nums[fast] != nums[fast+1]){
nums[slow+1] = nums[fast+1];
slow += 1;
}
fast += 1;
}
return slow+1;
}
}
- 移动零
给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。
示例:
输入: [0,1,0,3,12] 输出: [1,3,12,0,0]
# python
class Solution:
def moveZeroes(self, nums: List[int]) -> None:
"""
Do not return anything, modify nums in-place instead.
"""
slow = fast = 0
while(fast<len(nums)):
if nums[fast] != 0:
nums[slow] = nums[fast]
slow += 1
fast += 1
for i in range(slow,len(nums)):
nums[i] = 0
# Java
class Solution {
public void moveZeroes(int[] nums) {
int slow = 0;
for(int fast = 0; fast < nums.length; fast++){
if(nums[fast] != 0){
nums[slow++] = nums[fast];
}
}
for(int i = slow; i < nums.length; i++){
nums[i] = 0;
}
}
}
- 比较含退格的字符串
给定 S 和 T 两个字符串,当它们分别被输入到空白的文本编辑器后,判断二者是否相等,并返回结果。 # 代表退格字符。
注意:如果对空文本输入退格字符,文本继续为空。
示例 1:
输入:S = “ab#c”, T = “ad#c” 输出:true
解释:S 和 T 都会变成 “ac”。
示例 2:
输入:S = “ab##”, T = “c#d#” 输出:true
解释:S 和 T 都会变成 “”。
示例 3:
输入:S = “a##c”, T = “#a#c” 输出:true
解释:S 和 T 都会变成 “c”。
示例 4:
输入:S = “a#c”, T = “b” 输出:false
解释:S 会变成 “c”,但 T 仍然是 “b”。
# python
class Solution:
def backspaceCompare(self, s: str, t: str) -> bool:
def solve(s):
slow = fast = 0
while(fast<len(s)):
if (s[fast] != '#'):
s[slow] = s[fast]
slow += 1
else:
if slow:
slow -= 1
fast += 1
return s[0:slow]
s = solve(list(s))
t = solve(list(t))
return s==t
# Java
class Solution {
public boolean backspaceCompare(String s, String t) {
Solution test = new Solution();
char[] s1 = test.solve(s.toCharArray());
char[] t1 = test.solve(t.toCharArray());
System.out.println(s1);
System.out.println(t1);
boolean isEqual=true;
if(s1.length!=t1.length){
return false;
}
for(int i = 0; i < s1.length; i++){
if(s1[i] != t1[i]){
isEqual=false;
break;
}
}
if(isEqual){
return true;
}else{
return false;
}
}
public char[] solve(char[] s){
int slow = 0;
for(int fast = 0; fast<s.length; fast++){
if(s[fast] != '#'){
s[slow++] = s[fast];
}else{
if(slow > 0){
slow--;
}
}
}
return Arrays.copyOfRange(s,0,slow);
}
}
- 有序数组的平方
给你一个按 非递减顺序 排序的整数数组 nums,返回 每个数字的平方 组成的新数组,要求也按 非递减顺序 排序。
示例 1:
输入:nums = [-4,-1,0,3,10]
输出:[0,1,9,16,100]
解释:平方后,数组变为 [16,1,0,9,100]
排序后,数组变为 [0,1,9,16,100]
进阶:
请你设计时间复杂度为 O(n) 的算法解决本问题
# python
class Solution:
def sortedSquares(self, nums: List[int]) -> List[int]:
n = len(nums)
left, right, index = 0, n - 1, n - 1
result = [-1]*n
while(left<=right): # 最大的数一定在两边,用双指针每次挑出最大值
l = nums[left] ** 2
r = nums[right] ** 2
if(l >= r):
result[index] = l
left += 1
else:
result[index] = r
right -= 1
index -= 1
return result
# Java
class Solution {
public int[] sortedSquares(int[] nums) {
int n = nums.length;
int left = 0;
int right = n - 1;
int index = n - 1;
int[] result = new int[n];
while(left<=right){
if(nums[left]*nums[left]>=nums[right]*nums[right]){
result[index--] = nums[left]*nums[left++];
}else{
result[index--] = nums[right]*nums[right--];
}
}
return result;
}
}
滑动窗口
滑动窗口的思想:
用i,j表示滑动窗口的左边界和右边界,通过改变i,j来扩展和收缩滑动窗口,可以想象成一个窗口在字符串上游走。
步骤一
不断增加j使滑动窗口增大,直到窗口满足条件。
步骤二
不断增加i使滑动窗口缩小,将不必要的元素排除在外,使长度减小,直到碰到一个必须包含的元素,这个时候不能再扔了,再扔就不满足条件了,记录此时滑动窗口的长度,并保存最小值。
步骤三
让i再增加一个位置,这个时候滑动窗口肯定不满足条件了,那么继续从步骤一开始执行,寻找新的满足条件的滑动窗口,如此反复,直到j超出范围。
- 长度最小的子数组
给定一个含有 n 个正整数的数组和一个正整数 target 。
找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, …, numsr-1, numsr] ,并返回其长度。如果不存在符合条件的子数组,返回 0 。
示例 1:
输入:target = 7, nums = [2,3,1,2,4,3]
输出:2
解释:子数组 [4,3] 是该条件下的长度最小的子数组。
示例 2:
输入:target = 4, nums = [1,4,4]
输出:1
示例 3:
输入:target = 11, nums = [1,1,1,1,1,1,1,1]
输出:0
# python
class Solution:
def minSubArrayLen(self, target: int, nums: List[int]) -> int:
n = len(nums)
left = 0;
sum = 0;
result = float("inf") # 定义一个无限大的数
for i in range(n):
sum += nums[i]
while(sum >= target):
result = min(result,i-left+1)
sum -= nums[left]
left += 1
# if(result == float("inf")):
# return 0
# else:
# return result
return 0 if result == float("inf") else result
# Java
class Solution {
public int minSubArrayLen(int target, int[] nums) {
int n = nums.length;
int left = 0;
int sum = 0;
int result = Integer.MAX_VALUE;
for(int i = 0; i < n; i++){
sum += nums[i];
while(sum >= target){
result = Math.min(result,i-left+1);
sum -= nums[left++];
}
}
// if(result==Integer.MAX_VALUE){
// return 0;
// }else{
// return result;
// }
return result==Integer.MAX_VALUE ? 0 : result;
}
}
- 水果成篮
在一排树中,第 i 棵树产生 tree[i] 型的水果。
你可以从你选择的任何树开始,然后重复执行以下步骤:
把这棵树上的水果放进你的篮子里。如果你做不到,就停下来。
移动到当前树右侧的下一棵树。如果右边没有树,就停下来。
请注意,在选择一颗树后,你没有任何选择:你必须执行步骤 1,然后执行步骤 2,然后返回步骤 1,然后执行步骤 2,依此类推,直至停止。
你有两个篮子,每个篮子可以携带任何数量的水果,但你希望每个篮子只携带一种类型的水果。
用这个程序你能收集的水果树的最大总量是多少?
示例 1:
输入:[1,2,1]
输出:3
解释:我们可以收集 [1,2,1]。
示例 2:
输入:[0,1,2,2]
输出:3
解释:我们可以收集 [1,2,2]
如果我们从第一棵树开始,我们将只能收集到 [0, 1]。
示例 3:
输入:[1,2,3,2,2]
输出:4
解释:我们可以收集 [2,3,2,2]
如果我们从第一棵树开始,我们将只能收集到 [1, 2]。
示例 4:
输入:[3,3,3,1,2,1,1,2,3,3,4]
输出:5
解释:我们可以收集 [1,2,1,1,2]
如果我们从第一棵树或第八棵树开始,我们将只能收集到 4 棵水果树。
# python
class Solution:
def totalFruit(self, fruits: List[int]) -> int:
left = 0
result = 0
# temp = {}
temp = collections.Counter()
for i,x in enumerate(fruits): # 不断扩大右边界
# if temp.get(x)==None:
# temp[x] = 1
# else:
# temp[x] += 1
temp[x] += 1
while(len(temp)>=3): # 一旦树的种类超过两种,缩小左边的索引
temp[fruits[left]] -= 1
if temp[fruits[left]] == 0:
del temp[fruits[left]]
left += 1 # 有可能缩完left,接下来的left还是同种树,树的种数没减,故得放在while循环
result = max(result,i-left+1) # 记录各种水果树等于2的长度,第一次记录会有小于2的情况
return result
# Java
class Solution {
public int totalFruit(int[] fruits) {
int left = 0;
int result = 0;
Counter count = new Counter();
for(int i = 0; i < fruits.length; i++){
count.add(fruits[i],1);
while(count.size()>=3){
count.add(fruits[left],-1);
if(count.get(fruits[left])==0){
count.remove(fruits[left]);
}
left++;
}
result = Math.max(result,i-left+1);
}
return result;
}
}
class Counter extends HashMap<Integer, Integer> {
public int get(int k) {
return containsKey(k) ? super.get(k) : 0;
}
public void add(int k, int v) {
put(k, get(k) + v);
}
}
- 最小覆盖子串
给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串,则返回空字符串 “” 。
注意:
对于 t 中重复字符,我们寻找的子字符串中该字符数量必须不少于 t 中该字符数量。
如果 s 中存在这样的子串,我们保证它是唯一的答案。
示例 1:
输入:s = “ADOBECODEBANC”, t = “ABC”
输出:“BANC”
示例 2:
输入:s = “a”, t = “a”
输出:“a”
示例 3:
输入: s = “a”, t = “aa”
输出: “”
解释: t 中两个字符 ‘a’ 均应包含在 s 的子串中, 因此没有符合条件的子字符串,返回空字符串。
进阶:你能设计一个在 o(n) 时间内解决此问题的算法吗?
参考题解
# python
class Solution:
def minWindow(self, s: str, t: str) -> str:
need = collections.Counter()
for c in t:
need[c] += 1
needCNT = len(t)
left = 0
res = (0,float("inf"))
for i,c in enumerate(s):
if need[c] > 0:
needCNT -= 1
need[c] -= 1
while(needCNT == 0): # 步骤一:滑动窗口包含了所有T元素 步骤二:增加left,排除多余元素
if i-left<res[1]-res[0]: # 记录结果
res=(left,i)
if(need[s[left]] == 0): # 左边的字符在t中,否则值是负数
needCNT += 1 # left向右缩,还需要一个刚删掉的字符
need[s[left]] += 1 # 步骤三:left增加一个位置,寻找新的满足条件滑动窗口
left += 1
return '' if res[1]>len(s) else s[res[0]:res[1]+1]
# Java
class Solution {
public String minWindow(String s, String t) {
Counter need = new Counter();
for(int i = 0; i < t.length(); i++){
need.add(t.charAt(i),1);
}
int left = 0;
int needCNT = t.length();
int[] res = {0, Integer.MAX_VALUE};
for(int i = 0; i < s.length(); i++){
if(need.get(s.charAt(i))>0){ // s[i]包含t中的某个字符,讲need中的该字符数减1,还需匹配长度减1
needCNT -= 1;
}
need.add(s.charAt(i),-1);
while(needCNT==0){ // needCNT == 0 时s包含t所有字符
if ((i - left)<(res[1] - res[0])){
res[0] = left;
res[1] = i;
}
if (need.get(s.charAt(left)) == 0){ // 数量为负是多余的,为0则刚刚好,left右移则s[left]又得再找一个
needCNT += 1;
}
need.add(s.charAt(left),1); // 假如left位置的元素为-2,表示多余两个s[left],右移后多余剩1个,直至刚好为0,i再继续滑动
left++;
}
}
return res[1]>s.length() ? "" : s.substring(res[0],res[1]+1);
}
}
class Counter extends HashMap<Integer, Integer> {
public int get(int k) {
return containsKey(k) ? super.get(k) : 0;
}
public void add(int k, int v) {
put(k, get(k) + v);
}
}
我们会用i扫描一遍S,也会用left扫描一遍S,最多扫描2次S,所以时间复杂度是O(n).
- 螺旋矩阵
给你一个 m 行 n 列的矩阵 matrix ,请按照 顺时针螺旋顺序 ,返回矩阵中的所有元素。
示例 1:

输入:matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出:[1,2,3,6,9,8,7,4,5]
示例 2:
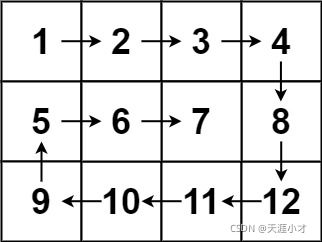
输入:matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出:[1,2,3,4,8,12,11,10,9,5,6,7]
# python
class Solution:
def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
m = len(matrix)
n = len(matrix[0])
left, right, up ,down = 0, n-1, 0, m-1
temp = []
while(left<=right and up<=down):
for i in range(left,right+1):
temp.append(matrix[up][i])
for j in range(up+1,down+1):
temp.append(matrix[j][right])
if(up != down):
for i in range(right-1,left,-1):
temp.append(matrix[down][i])
if(left != right):
for j in range(down,up,-1):
temp.append(matrix[j][left])
left += 1
right -= 1
up += 1
down -= 1
return temp
# Java
class Solution {
public List<Integer> spiralOrder(int[][] matrix) {
int m = matrix.length;
int n = matrix[0].length;
int left = 0, right = n - 1, up = 0, down = m - 1;
//int[] temp = new int[m*n];
List<Integer> temp = new ArrayList<Integer>();
//int count = 0;
while(left <= right && up <= down){
for(int i = left; i <= right; i++){
//temp[count++] = matrix[up][i];
temp.add(matrix[up][i]);
}
for(int i = up + 1; i <= down; i++){
//temp[count++] = matrix[i][right];
temp.add(matrix[i][right]);
}
if(up != down){
for(int i = right - 1; i > left; i--){
//temp[count++] = matrix[down][i];
temp.add(matrix[down][i]);
}
}
if(left != right){
for(int i = down; i > up; i--){
//temp[count++] = matrix[i][left];
temp.add(matrix[i][left]);
}
}
left++;
right--;
up++;
down--;
}
return temp;
}
}
- 螺旋矩阵II
给你一个正整数 n ,生成一个包含 1 到 n2 所有元素,且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。
输入:n = 3
输出:[[1,2,3],[8,9,4],[7,6,5]]
示例 2:
输入:n = 1
输出:[[1]]
# python
class Solution:
def generateMatrix(self, n: int) -> List[List[int]]:
left, right, up, down = 0, n-1, 0, n-1
matrix = [[0]*n for _ in range(n)]
count = 1
while(left<right and up<down):
for i in range(left, right):
matrix[up][i] = count
count += 1
for j in range(up, down):
matrix[j][right] = count
count += 1
for i in range(right, left, -1):
matrix[down][i] = count
count += 1
for j in range(down, up, -1):
matrix[j][left] = count
count += 1
left += 1
right -= 1
up += 1
down -= 1
if(n % 2):
matrix[n//2][n//2] = count
return matrix
# Java
class Solution {
public int[][] generateMatrix(int n) {
int left = 0, right = n-1, up = 0, down = n-1;
int[][] matrix = new int[n][n];
int count = 1;
while(left < right && up < down){
for(int i = left; i < right; i++){
matrix[up][i] = count++;
}
for(int j = up; j < down; j++){
matrix[j][right] = count++;
}
for(int i = right; i > left; i--){
matrix[down][i] = count++;
}
for(int j = down; j > up; j--){
matrix[j][left] = count++;
}
left++;
right--;
up++;
down--;
}
if(n % 2 != 0){
matrix[n/2][n/2] = count;
}
return matrix;
}
}
