并行与分布式计算 第8章 并行计算模型

并行与分布式计算 第8章 并行计算模型

8.1 并行算法基础

8.1.1 并行算法的定义

并行算法：适合于在各种并行计算机上求解问题和处理数据的算法，它是一些可同时执行的诸进程的集合，这些进程相互作用和协调动作从而达到对给定问题的求解。

8.1.2并行算法的分类

分类标准	运算类型
数值计算 vs 非数值计算	数值计算涉及数字和数学运算，如矩阵运算、多项式求解等。非数值计算涉及非数值数据的处理和操作，如排序、选择、搜索、匹配、图论等。
同步运算 vs 异步运算	同步运算需要等待其他进程或操作结果，异步运算不需要等待其他进程的完成。
确定运算 vs 随机运算	确定运算的每一步都能明确指示下一步应该如何进行，随机运算的某些步骤涉及随机选择或随机参数。

8.1.3算法的复杂度

并行算法的复杂性度量指标1

运行时间t(n):在给定的模型上求解输入规模为n的给定问题所需时间，即
算法从第一台处理机开始执行到最后一台处理机执行中止所需时间。
** t(n)包括两个部分：**

• 计算时间tc：在某一处理器执行运算所需时间；
• 通信时间tr：数据从源处理机到目的处理机所需传送时间，算法在整个
  执行期间能传送的报文总数称为通信复杂度。

并行算法的复杂性度量指标2

• 处理机数p(n):求解给定问题所需的处理机数
• 并行算法的成本c(n) =t(n) x p(n)
• 成本最优（Cost Optimal）：c(n)=t(n)*p(n)=串行计算的步数（节拍数）
• 工作量最优：功耗低、环保

并行算法的复杂性度量指标3（Brent定理）
令W(n)是某并行算法A在运行时间T(n)内所执行的运算量，则A使用p台处理器可在t(n)=O(W(n)/p+T(n))时间内执行完毕
W(n)和c(n)密切相关：c(n) =t(n) x p= O(W(n)/p+T(n)) x p = O(W(n) +p x T(n))， 因此当p=O(W(n)/T(n))时，c(n) = O(W(n))，W(n)和c(n)两者是渐近一致的；
推论：对于任意的p，c(n)>W(n)，说明算法在运行过程中不一定能够充分利用处理器。

8.2 并行计算模型

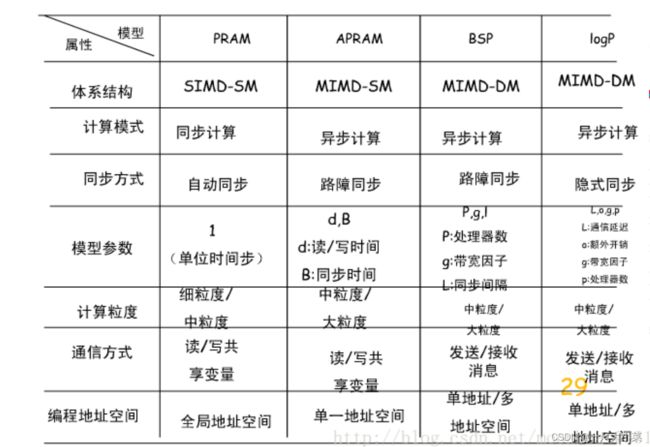
并行计算模型通常指从并行算法的设计和分析出发，将各种并行计算机（至少某一类并行计算机）的基本特征抽象出来，形成一个抽象的计算模型。从更广的意义上说，并行计算模型为并行计算提供了硬件和软件界面，在该界面的约定下，并行系统硬件设计者和软件设计者可以开发对并行性的支持机制，从而提高系统的性能。

8.2.1 PRAM (SIMD-SM)模型

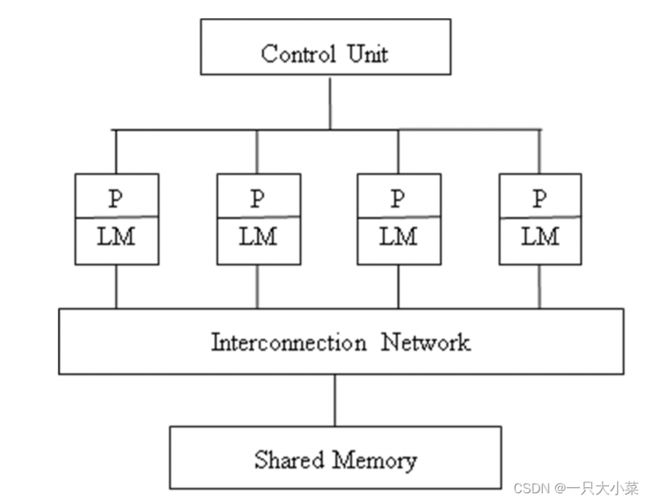
并行随机存取机器（Parallel Random Access Machine, PRAM）模型，也称为 SIMD-SM模型（共享存储的SIMD模型）

• 一个集中的共享存储器，假设其容量M无限大；
• N个功能相同的处理器，每个处理器具有简单的算术运算和逻辑判断能力，每个处理器都具有局部存储器LM。
• 所有指令均按照操作，在每一个计算步内，任一个处理器均可通过对共享存储器的某共享单元读写，同其他任一处理器交换数据，因此要求所有处理器共享单一的数据地址空间；
• 每个处理器内部都没有控制器组件，所有的处理器共享一个控制器， 因此要求所有处理器共享单一的程序地址空间；
• 采用隐式同步机制，诸如处理器间通讯、存储管理、进程同步、存储 带宽和延迟等并行机的低级操作细节均隐含于模型中。

PRAM (SIMD-SM)计算模式

• PRAM-EREW互斥读互斥写（最弱）
• PRAM-CREW并发读互斥写（居中）
• PRAM-CRCW并发读并发写（最强）
  • C代表Concurrent，允许并发操作
  • E-代表Exclusive，禁止并发操作

PRAM (SIMD-SM)复杂度分析
TEREW = O(TCREW *log p) = O(TCRCW * log p)

如果一个算法在PRAM-CREW或PRAM-CRCW上的时间复杂度为T，则这个算法可以在PRAM-EREW上以 时间复杂度为logp x T运行。

PRAM-CRCW的分类
• Common PRAM-CRCW：仅允许所有处理器同时写入相同数据
• Priority PRAM-CRCW：仅允许优先级最高的处理器写入
• Arbitrary PRAM-CRCW：允许任意处理器自由写入

(MIMD-SM)模型
异步并行随机存取机器（Asynchronous Parallel Random Access Machine, APRAM）模型，也称为MIMD-SM模型，也称为分相（Phase）PRAM模型。

• 一个集中的共享存储器，假设其容量M无限大；
• N个处理器，每个处理器内部，有简单的算术运算和逻辑判断电路，有独立的控制器，有局部存储器LM，有局部时钟；
• 处理器之间的通信要通过共享存储器来完成，因此要求所有处理器共享单一的数据地址空间；
• 每个处理器内部都有独立的控制器组件，因此要求所有处理器都有独立得程序地址空间；
• 异步操作+显式同步。系统没有全局时钟，每个处理器异步的执行局 部程序，处理器之间的时间依赖关系（例如，通过共享变量的读写操作实 现通信等）需要在各个处理器的局部程序中加入同步路障（Synchronization Barrier）来实现，两次同步路障的时间间隔称为一个相（phase）

APRAM (MIMD-SM)计算模式分析
• 整个计算过程系由一系列同步路障分开的多个全局相所组成。
• 在每个全局相内，每个处理器异步的运行其局部程序；
• 每个局部程序中的最后一条指令是一条同步路障指令；
• 各个处理器均可异步地读取和写入全局存储器，但在同一个全局相内不允许两个处理器访问同一存储单元。
• 程序内指令的分类：全局同步，全局读/写，局部操作

APRAM (MIMD-SM)复杂度分析：
• 设局部操作为单位时间；
• 全局读/写平均时间为d，d随着处理器数目的增加而增加；
• 同步路障时间为B=B§，它是处理器数p的非降函数，通常
处理器越多导致同步时间越长。
• 设Ti为第i个全局相内各处理器执行时间最长者；
• 则T=T1+T2+…+Tn+ B x (n-1)

8.2.3 BSP (MIMD-DM)模型

块同步（Bulk Synchronization Parallel）模型，也称为MIMD- DM（distributed memory）模型，也称为大同步模型、桥模型， 桶同步并行模型。
• 系统中有p个计算节点，每个计算节点内部有独立的运算 器，独立的控制器，独立的存储器，独立的局部时钟；因此， 每个处理器有独立的数据地址空间和程序地址空间，可以异步 的执行局部程序；
• 系统中有一个路由器，该路由器连接所有计算节点，实施计算节点之间点到点的消息传递，该路由器的吞吐率和延迟是有限的，吞吐率th（字节每秒），传输延迟tl（秒）；
• 系统中有一个路障同步器，路障同步器每隔时间间隔L完 成一次全局路障同步操作，以实现计算节点之间的时间依赖关 系（例如，通过共享变量的读写操作实现通信等）。

BSP（MIMD-DM）复杂度分析：
• 设Wk为第k个超级步内各节点局部程序中本地计算运行时间最 长者；
• 设Hk为第k个超级步内各节点局部程序中收发消息个数最多者 的收发操作执行时间；
• 设每次全局同步路障的开销为B； • 设每个数据包大小q个字节；
• 则Hk=h*(tl （传输延迟） +q/th（吞吐率）) • 一个超级步内的总时间开销为Tk=Wk + Hk +B； (Tk需要小于 等于L，效率为Tk/L)
• s个超级步内的总时间开销为T=W1+W2+…+Ws +
H1+H2+…+Hs + s x B；（T需要小于等于sL，效率为T/(sL)）
BSP与MapReduce对比
• 执行机制：MapReduce是一个数据流模型，每个任务只是对输入数
据进行处理，产生的输出数据作为另一个任务的输入数据，并行任
务之间独立地进行，串行任务之间以磁盘和数据复制作为交换介质
和接口。
• BSP是一个状态模型，各个子任务在本地的子图数据上进行计算、
通信、修改图的状态等操作，并行任务之间通过消息通信交流中间
计算结果，不需要像MapReduce那样对全体数据进行复制。
• MapReduce的设计初衷：解决大规模、非实时数据处理问题。"大规
模"决定数据有局部性特性可利用（从而可以划分）、可以批处理；
"非实时"代表响应时间可以较长，有充分的时间执行程序。而BSP
模型在实时处理有优异的表现。这是两者最大的一个区别。

8.2.4LogP（MIMD-DM）模型

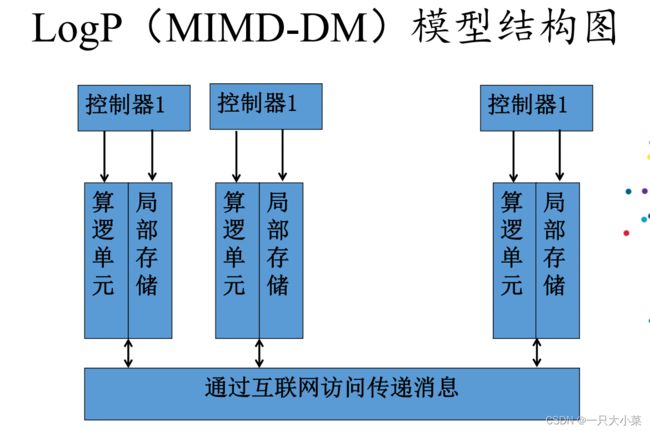
• LogP是使用L,O,G,P四个参数来描述的一种面向分布式存储 器、点对点通信的多计算机系统的并行计算模型。
• L (Latency) ：表示信息从源节点到目的节点所需的时间；
• O (Overhead) ：表示节点接收或发送一条消息所需额外开销 （操作系统开销和网络软件开销），并且在此期间节点不 能做作任何操作；
• G (Gap)：表示节点连续进行两次发送或接收消息之间必须 有的时间间隔，超过此间隔则数据包会因拥塞而被网络丢 弃，因此实际上此参数是对网络的限制而非对节点的限制；
• P (Processor) ：表示节点的数目

LogP（MIMD-DM）模型的特点

• 系统中有p个计算节点，每个计算节点内部有独立的
运算器，独立的控制器，独立的存储器，独立的局部时钟；
因此，每个处理器有独立的数据地址空间和程序地址空间，
可以异步的执行局部程序；
• 系统中有一个大型互连网络（多个路由器节点组成的
数据交换阵列），该互连网络连接所有节点，实施节点之
间点到点的消息传递，该互连网络的带宽和延迟是有限的，
带宽为g的倒数（字节每秒），传输延迟L（秒）；
• 通过节点间的个体消息传递实现同步操作，一旦消息
到达了处理器就可以立即使用。

LogP模型小结

• 即时通信
  • LogP不再把所有的计算和通信视为一个整体行为，而是一个单独的进程的个体活动；它让每个进程按需排布计算操作和消息收发，一旦收到消息立即可以使用；
• 同步开销 LopP不需要路障同步器，将路障同步的开销降低为两个进程之间的信息收发时间差；
• 硬件气泡
  •节点执行计算操作时网络资源空闲，节点执行消息收发时计算资源空闲，非阻塞进程不必等待阻塞进程避免了节点空转；可使用节点内多进程/多线程来填充气泡
• Tradeoff
  • 编程的随意性v.s.性能的可预测性

Multi-BSP (多层架构)模型

multi-BSP从两个方向拓展了BSP :
• multi-BSP model是一个层次模型，它可以表示出单芯片或多芯片架构中的多个memory或多个cache。
• 在每一层中，multi-BSP都将存储大小作为一个参数。

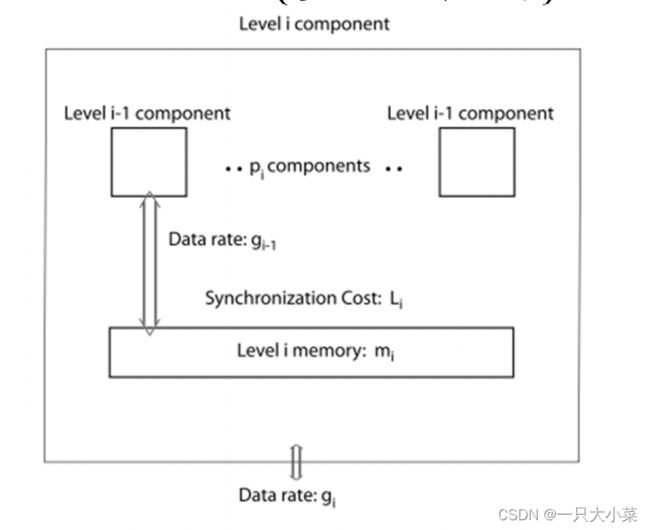
Multi-BSP model实际上是一个深度为D的树，内部节点表示memory 和cache，叶子节点表示处理器，每一层有四个参数（pi, gi, Li, mi）：
• pi表示子组件的数量，
• gi表示通信带宽，
• Li表示同步成本，
• mi表示memory或cache的大小。

Multi-BSP (多层架构)模型的架构