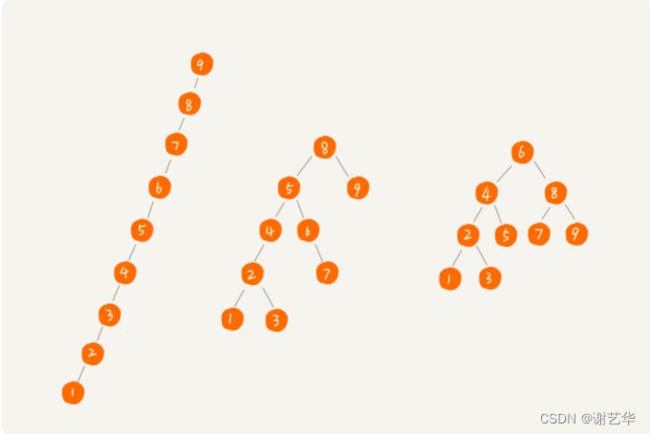【追求卓越11】算法--二叉树

引导

        接下来的几节我们开始介绍非线性的数据结构--树。树的内容比较多也比较复杂。本节，我们只需要了解关于树的一些基本概念。以及再进一步了解树的相关内容--搜索二叉树。该类型二叉树在工作中，是我们常接触的。该节我们介绍关于搜索二叉树的相关操作：查找，插入，删除。

什么是树？

关于树的定义：（摘自百度百科）

1. 每个元素称为结点（node）
2. 有一个特定的结点被称为根结点或树根（root）
3. 除根结点之外的其余数据元素被分为m（m≥0）个互不相交的集合T1，T2，……Tm-1，其中每一个集合Ti（1<=i<=m）本身也是一棵树，被称作原树的子树（subtree）

说实话，这段定义我看了好几遍才能理解，对于刚接触的同学，结合图来理解是最好的了。

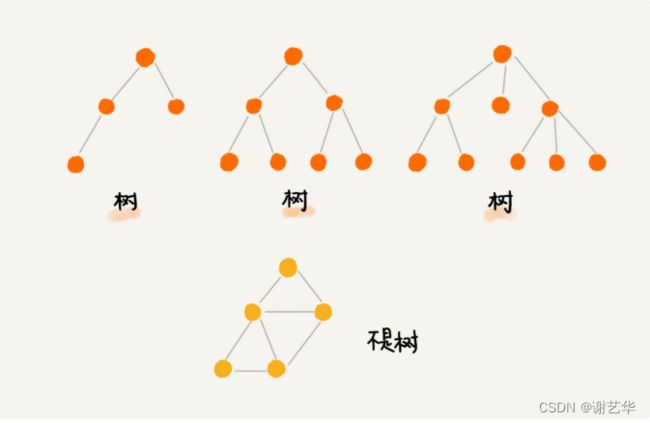
树中有很多需要我们了解的名词，我们结合下面的树来介绍：

        在上图中,A节点就是B节点的父节点，B节点是A节点的子节点。B，C,D这三个节点有共同的父节点，他们是兄弟节点。我们把没有父节点的节点称作为根节点，也就是图中的E节点。我们把没有子节点的的节点称作叶子节点或叶节点。

此外还有三个相似的概念：高度，深度，层。

节点的高度：节点到叶子节点最长路径。比如，上图中A节点的高度就是2.

节点的深度：根节点到节点的所经历的边数。比如，上图中B节点的深度是2.

节点的层：节点的深度+1。比如，上图中B子节点的层是3.

树的高度：根节点的高度。比如，上图中的树的高度是3.

以上就是关于树的部分名词定义了。但是我们工作中常接触的是二叉树。接下来，我们来正式进入今天的主题。

二叉树

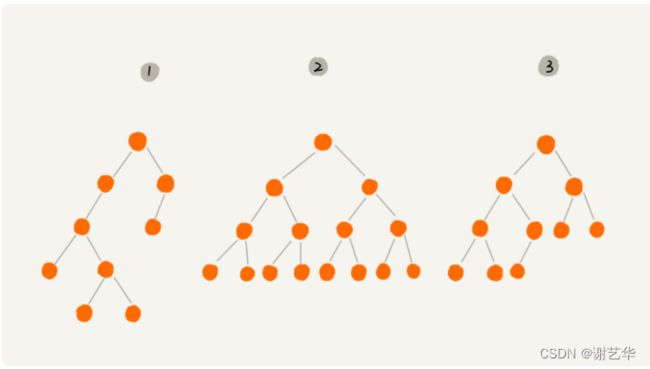
        二叉树顾名思义，每个节点最多有两个分支，即仅有两个子节点。同理，有四个，八个分支的树就是四叉树，八叉树。是不是很容易理解？如图：

        上图中三个树都是二叉树，但是有两个树有比较特殊，需要注意。

        其中2号树中，叶子节点都在最低层，并且除了叶子节点，每个节点都有左右两个字节点。这种二叉树称作为满二叉树。

        其中3号树中，叶子节点在最底下两层，最后一层的叶子节点都是靠左排列，并且除了最后一层，其他层的节点个数达到最大数，这种树称作完全二叉树。这个解释我觉得还不是很清晰，摘自百度百科：对于深度为K的，有n个结点的二叉树，当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树

        到了这里，你可能会有疑问：满二叉树很容易理解，是二叉树的一种特例。但是完全二叉树存在的意义是什么？

二叉树的存储方式

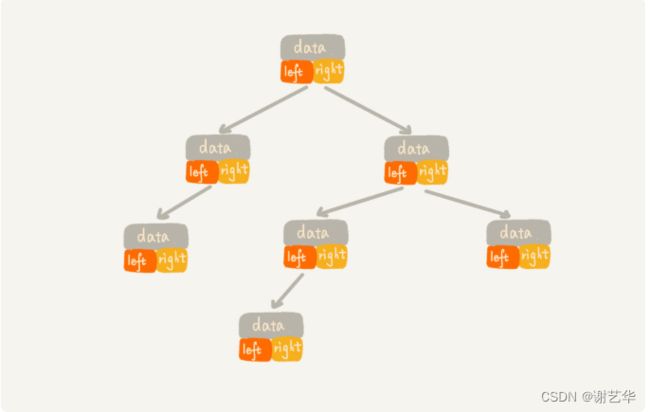
        我们常见的存储方式是基于指针或者引用的二叉链式存储法。他比较简单和直观，每个节点有一个数据段和两个左右指针。如图：

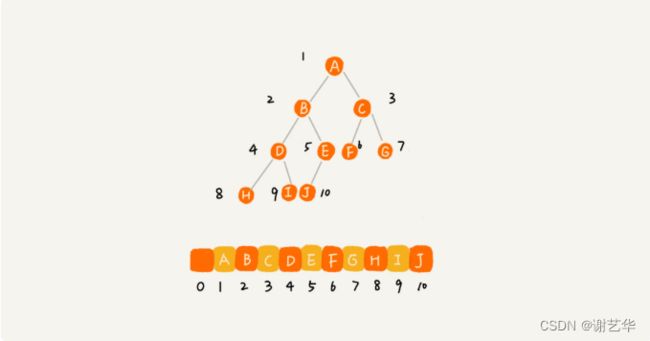
        另一种就是基于数组的顺序存储法。我们把根节点存储在下标i=1的位置，那左子节点存储的下标2 * i=2的位置，右子节点存储的下标2 * i+1的位置。

        根据这样的存储方式，刚刚的完全二叉树仅仅会浪费下标未0的空间，若不是完全二叉树就会出现浪费内存空间的现象。如图：

        所以对于完全二叉树，使用数组进行存储是最省内存的一种方式。因为顺序存储方式比链式存储方式更生内存，它不需要每个节点保存两个指针变量。

二叉树的遍历

对于二叉树的遍历，这个也是非常常见的面试题。常见的遍历方式是前序遍历，中序遍历，后序遍历。

前序遍历：对树中任意节点，先打印这个节点，然后打印它的左子树，最后打印右子树。

中序遍历：对于树中任意节点，先打印这个节点的左子树，然后打印该节点，最后打印右子树。

后序遍历：对于树中任意节点，先打印这个节点的左子树，然后打印右子树，最后打印改节点。

对于遍历，实现方式也很简单，这里仅仅给出伪代码

void preOrder(Node* root) {   if (root == null) return;   print root // 此处为伪代码，表示打印root节点   preOrder(root->left);   preOrder(root->right); } void inOrder(Node* root) {   if (root == null) return;   inOrder(root->left);   print root // 此处为伪代码，表示打印root节点   inOrder(root->right); } void postOrder(Node* root) {   if (root == null) return;   postOrder(root->left);   postOrder(root->right);   print root // 此处为伪代码，表示打印root节点 }

每个节点最多被访问两次，故时间复杂度是O(n)。

搜索二叉树

        搜索二叉树又称为二叉查找树。顾名思义，二叉查找树是为了快速查找而诞生的。它不仅仅支持快速查找，还支持插入，删除。

定义：二叉查找树要求，在树中任意一个节点，其左子树中的每个节点的值，都要小于这个节点的值。而右子树节点的值都大于这个节点的值。

可参考下图：

搜索二叉树的查找

1. 先一个节点（一般是root节点），判断是否是我们要查找的数据？
2. 如果要查找的数据比该节点的大，我们就在右子树中继续查找
3. 如果要查找的数据比该节点的小，我们就在左子树中继续查找
4. 若未查找到，则返回空

从上面的思路可以看出，我们可以用递归或者循环来实现，下面贴上代码(由于环境原因，代码都没有运行，不过代码逻辑应该是这样的)：

typedef strcut node{     int data;     struct node left;     struct node right; }Node; / *while 循环* / Node * BinarySearchTree(Node* root , int target) {     Node * p = root;     while(p != NULL)     {         if(p.data == target)             return p;         else if (p.data > target)             p = p.left;         else             p = p.right;     }     return NULL; } / *递归* / Node * BinarySearchTree(Node* root , int target) {     if(root == NULL)         return NULL;     if(root.data == target)     {         return root;     }     else if(root.data > target)     {         return BinarySearchTree(root.left,target);     }     else if(root.data < target)     {         return BinarysearchTree(root.right,target);     } }

1. 搜索二叉树的插入

        插入操作和查找操作类似，新插入的数据一般都是保存在叶子节点上的。这句话，我刚开始是抱有怀疑态度，通过自己的思考也就理解了。建议大家先理解这句话的意思。

若知道了新插入数据都是保存在叶子节点上的，那么插入操作的思路也就简单了。

思路：

1. 先获取一个节点，和插入数据比较哪个要大？
2. 若要插入的数据比节点的值大，并且右子树为空，即直接将数据插入到该节点的右子节点中。若不为空，继续遍历右子树
3. 若要插入的数据比节点的值小，并且左子树为空，即直接将数据插入到该节点的左子节点中。若部位空，继续遍历左子树

typedef strcut node{     int data;     struct node left;     struct node right; }Node; int BinarySearchInsert(Node * root , int target) {     Node * p = root ;     while(p != NULL)     {         if(p.data < target)         {             if(p.right == NULL)             {                 p.right = newNode(target);                 return 0;             }             p = p.right;         }         else         {             if(p.left == NULL)             {                 p.left = newNode(target);                 return 0;             }             p = p.left;         }     }     return -1; }

搜索二叉树的删除操作

搜索二叉树的删除操作就比较复杂了，因为删除之后，你必须要保证剩下的树结构满足搜索二叉树定义。其情况大致可以分为以下三种：

1. 删除节点没有子节点。删除一个节点，我们需要先找到这个节点，我们可以使用查找操作的逻辑。若删除节点没有子节点，也就不会影响树的结构。直接删除即可。将其父节点指向该节点的指针，指向NULL；
2. 删除的节点有一个子节点。将删除节点的父节点指向该节点的指针修改为指向子节点即可。
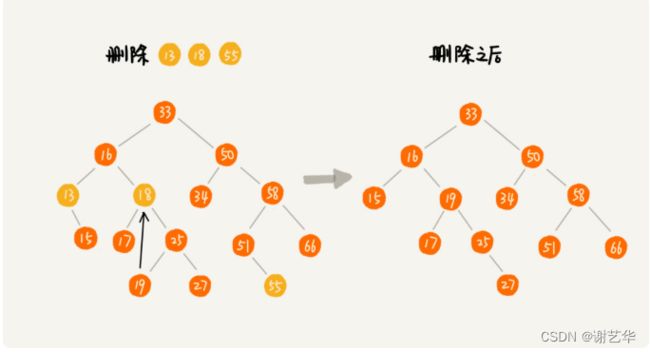
3. 删除节点有两个子节点。将删除节点的右子树中最小节点删除，并替换为该删除节点即可。这个可能比较抽象，可参数下图,删除18这个节点：

typedef strcut node{     int data;     struct node left;     struct node right; }Node; int BinarySearchDelete(Node * root , int target) {     Node * p = root;     Node * father = NULL；     Node * minfather = NULL;     Node * min = NULL;     while(p != NULL && p.data != target)     {         father = p; / *保存父节点* /         if(p.data < target)             p = p.left;         else             p = p.right;     }     if(p == NULL)         return -1;/ *not find target* /     / *删除节点有两个子节点* /     if(p.left != NULL && p.right != NULL)     {         minfather = p;         min = p.right;         while(min.left != NULL )             minfather = min;             min = min.left;         / *至此找到删除节点右子树中的最小节点* /         p.data = min.data; / *这里我觉得使用memcpy(p,min,sizeof(Node))较好* /         / *将删除的点变为只有一个或没有子节点* /         p = min;         father = minfather;     }     / *至此，p表示删除的节点，father表示删除节点的父节点，并且删除节点不会有两个子节点* /     Node * child = NULL;     if(p.left != NULL)         child = p.left;     else if(p.right != NULL)         child = p.right;     if(father == NULL)/ *删除的是root节点* /         memcpy(root,child,sizeof(Node));     else if(father.left == p)         father.left = child;     else         father.right = child;     free(p); }

搜索二叉树的中序遍历

        搜索二叉树有一个非常强大的特性，那就是通过中序遍历，即可输出有序的数据序列，时间复杂度是O(n),非常高效。

如何支持重复数据

上面的操作，我们都是假设没有重复数据，但是显示工作中我们总会遇到相同key的节点(key表示作为搜索二叉树依据)。针对相同键值的节点，我们又有哪些方式处理呢？

1. 利用数组或链表进行扩容，将相同键值的数据储存到同一个节点上。
2. 每个节点只保存一个数据。在插入的过程中，如果遇到一个节点的值，与要插入的值相同。我们就将这个要插入的数据放到这个节点的右子树。也就是将这个新插入的数据当作大于这个节点的值来处理。后续的删除都是按照这个逻辑处理

二叉查找树的时间复杂度

实际上二叉树的形态各式各样，即使同一组数据，也可以有不同的形态。如图：

第一种情况完全退化成了链表，时间复杂度为O(n)，第三种的效果应该会好一些。其实，我们可以知道时间复杂度其实跟树的高度成正比。也就是O(height)。根据完全二叉树可知，L 的范围是[log2(n+1), log2n +1]。这样就极大的提高了效率。因此我们能在实际工作中需要无论怎么删除或增加，都可以保证树的平衡。红黑树就是这样的一种树。时间复杂度为O(logn)

搜索二叉树相较于散列表的优点

虽然散列表在的时间复杂度达到了O(1),而查找二叉树在理想情况下，也是O(logn)。那么为什么，我们工作中，树的使用要高于散列表呢？

1. 散列表是无序存储，如果要输出有序的数据，需要先进行排序。而对于二叉树查找而言，我们仅需中序遍历就可以得到有序序列。
2. 散列表扩容是耗时较多（虽然我们有一些优化手段，分时），而且当遇到散列冲突时，性能不稳定。虽然搜索二叉树也不稳定，但我们在工作中常使用的是平衡二叉查找树。
3. 因为散列冲突的存在，散列表的时间复杂度并不一定比logn小。实际查找速度不一定比O(logn)快。另外还有哈希函数的耗时。
4. 综上几点，树在某些方面还是优于散列表的。

总结

        本节开始接触树的内容，了解到父节点，子节点，兄弟节点，根节点，叶子节点，高度，深度，层等概念

        树的种类有很多，工作中，我们常接触的就是二叉树。我们也介绍了完全二叉树和满二叉树的概念。以及二叉树存储的方式有基于指针的链式存储方式和基于数组的顺序存储方式。其中完全二叉树使用数组是最节省内存的方式。

        绍了什么是搜索二叉树，以及搜索二叉树的删除，增加，查找的的逻辑。

        也简单介绍了，当有相同的键值时，我们该如何处理：利用数组或链表扩容。或者默认为大于该节点。

        最后我们讲解了二叉树的三种遍历方式：前序遍历，中序遍历，后序遍历。以及代码的是实现方式。树结构相对于散列表的优势。