机器学习之贝叶斯分类器

贝叶斯决策论(Bayesian decision theory)是概率框架下实施决策的基本方法。对分类任务来说，在所有相关概率都己知的理想情形下，贝叶斯决策论考虑如何基于这些概率和误判损失来选择最优的类别标记。

1、相关术语和算法

1.1、贝叶斯决策论

决策论中将期望损失称为风险（risk）。
贝叶斯判定准则(Bayes decision rule)：为最小化总体风险，只需在每个样本上选择那个能使条件风险最小的类别标记，称为贝叶斯最优分类器(Bayes optimal classifier) 。
欲使用贝叶斯判定准则来最小化决策风险，首先要获得后验概率P(c | x)。
机器学习所要实现的是基于有限的训练样本集尽可能准确地估计出后验概率。大体来说，主要有两种策略：
给定样本x，可通过直接建模P(c | x)来预测分类c，这样得到的是判别式模型(discriminative models); 比如：决策机、SVM等。
也可先对联合概率分布P(x,c)建模，然后再由此获得P(c | x)，这样得到的是生成式模型(generative models)。
对生成式模型来说，基于贝叶斯定理，后验概率P(c | x)可写为
$$P(c\mid x)=\frac{P(c)P(x\mid c)}{P(x)}$$
其中，P( c ) 是类"先验"(prior)概率；P(x | c)是样本x相对于类标记c的类条件概率(class-conditional probability) ，或称为"似然" (likelihood)；P(x) 是用于归一化的"证据" (evidence) 因子，对给定样本x，证据因子P(x) 与类标记无关，因此估计P(c I x) 的问题就转化为如何基于训练数据D 来估计先验P( c ) 和似然P(x I c)。
类先验概率P( c ) 表达了样本空间中各类样本所占的比例，根据大数定律，当训练集包含充足的独立同分布样本时， P( c ) 可通过各类样本出现的频率来进行估计。
对类条件概率P(x I c) 来说，由于它涉及关于x所有属性的联合概率，直接根据样本出现的频率来估计将会遇到严重的困难。估计类条件概率的一种常用策略是先假定其具有某种确定的概率分布形式，再基于训练样本对概率分布的参数进行估计。

1.2、极大似然估计

估计类条件概率的一种常用策略是先假定其具有某种确定的概率分布形式，再基于训练样本对概率分布的参数进行估计。
根据数据采样来估计概率分布参数的经典方法是极大似然估计(Maximum Likelihood Estimation，简称MLE)，通过极大似然法得到的正态分布均值就是样本均值，方差就是$(x-{\hat{\mu }}_c)(x-{\hat{\mu }}_c{)}^T$的均值。
注意：估计结果的准确性严重依赖于所假设的概率分布形式是否符合潜在的真实数据分布。

1.3、朴素贝叶斯分类器

朴素贝叶斯分类器(naive Bayes classifier) 采用了"属性条件独立性假设" (attribute conditional independence assumption)：对已知类别，假设所有属性相互独立。从而避免了训练样本所有属性的联合概率难以估计的问题。
“半朴素贝叶斯分类器” (semi-naive Bayes classifiers)
半朴素贝叶斯分类器的基本想法是适当考虑一部分属性问的相互依赖信息。常用策略是"独依赖估计" (One-Dependent Estimator，简称ODE) ，所谓"独依赖"就是假设每个属性在类别之外最多仅依赖于一个其他属性。

1.4、贝叶斯网

贝叶斯网(Bayesian network)亦称"信念网" (belief network) ，它借助有向无环图(Directed Acyclic Graph，简称DAG)来刻画属性之间的依赖关系，并使用条件概率表(Conditional Probability Table ， 简称CPT)来描述属性的联合概率分布。
贝叶斯网B 由结构 G 和参数 $\Theta$ 两部分构成，即B =( G，$\Theta$) 。网络结构G 是一个有向无环图，用于描述样本属性及直接依赖关系；参数$\Theta$定量描述这种依赖关系。
求解：评分搜索是常用办法。
具体来说，我们先定义一个评分函数(score function) ，以此来评估贝叶斯网与训练数据的契合程度，然后基于这个评分函数来寻找结构最优的贝叶斯网。
贝叶斯网的近似推断常使用吉布斯采样(Gibbs sampling)

1.5、EM算法

EM(Expectation-Maximization) 算法使用两个步骤变替计算：
第一步是期望(E)步，利用当前估计的参数值来计算对数似然的期望值；
第二步是最大化(M)步，寻找能使E 步产生的似然期望最大化的参数值。然后，新得到的参数值重新被用于E 步。
EM 算法可看作用坐标下降(coordinate descent) 法来最大化对数似然下界的过程。

1.6、概率和似然的再理解

先验概率：通过经验来判断事情发生的概率，比如说“贝叶死”的发病率是万分之一，就是先验概率
后验概率：后验概率就是发生结果之后，推测原因的概率。比如说某人查出来了患有“贝叶死”，那么患病的原因可能是 A、B 或 C。**患有“贝叶死”是因为原因 A 的概率就是后验概率。**它是属于条件概率的一种。
条件概率：事件 A 在另外一个事件 B 已经发生条件下的发生概率，表示为 P(A|B)。比如原因 A 的条件下，患有“贝叶死”的概率，就是条件概率。
似然函数（likelihood function）：
似然在这里就是可能性的意思。在数理统计学中，似然函数是一种关于统计模型中的参数的函数，表示模型参数中的似然性。

在统计学中，“似然性”和“概率”又有明确的区分。概率用于在已知一些参数的情况下，预测接下来的观测所得到的结果，而似然性则是用于在已知某些观测所得到的结果时，对有关事物的性质的参数进行估计。

2、Sklearn代码实现

Sklearn库有关贝叶斯算法的介绍

• GaussianNB 实现了运用于分类的高斯朴素贝叶斯算法。特征的可能性(即概率)假设为高斯分布。
• MultinomialNB 实现了服从多项分布数据的朴素贝叶斯算法。
• ComplementNB实现了补充朴素贝叶斯(CNB)算法。CNB是标准多项式朴素贝叶斯(MNB)算法的一种改进，特别适用于不平衡数据集。
• BernoulliNB 实现了用于多重伯努利分布数据的朴素贝叶斯训练和分类算法，即有多个特征，但每个特征 都假设是一个二元 (Bernoulli, boolean) 变量。

朴素贝叶斯模型包括 MultinomialNB, BernoulliNB, 和 GaussianNB 等都提供了 partial_fit 方法，可以动态的增加数据，用于解决整个训练集不能导入内存的大规模分类问题。
示例：鸢尾花数据集分类任务

import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.model_selection import train_test_split
import sklearn.naive_bayes as nb
import sklearn.metrics as sm


def naive_bayes_train():
    """
    朴素贝叶斯算法 - 高斯分布
    :return:
    """
    # 加载数据
    iris = datasets.load_iris()
    x = iris.data
    y = iris.target
    # 划分训练集和测试集
    x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=37, test_size=0.2)

    # 创建模型，高斯朴素贝叶斯算法
    model = nb.GaussianNB()
    # 模型训练
    model.fit(x_train, y_train)
    # 模型评估
    pred_y = model.predict(x_test)
    acc = model.score(x_train, y_train)
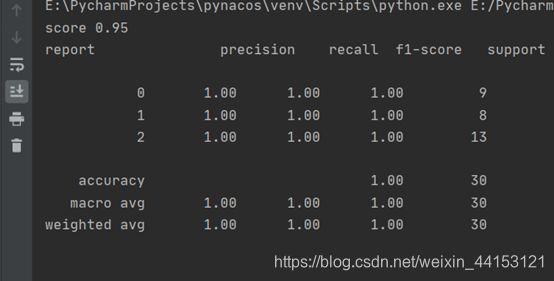
    print('score', acc)
    # 分类报告
    print('report', sm.classification_report(y_test, pred_y))

    # 绘制测试样本的散点图
    plt.title('Iris GaussianNB Classification')
    plt.xlabel(iris.feature_names[0], fontsize=14)
    plt.ylabel(iris.feature_names[1], fontsize=14)
    plt.tick_params(labelsize=10)
    plt.scatter(x_test[:, 0], x_test[:, 1], c=pred_y, cmap='brg', s=80)
    plt.show()


if __name__ == '__main__':
    # 朴素贝叶斯算法
    naive_bayes_train()

运行结果，如下：


从控制台输出可看出准确率等都是1，说明分类完全正确。只可惜训练数据集得分才0.95