leetcode练习一:数组(二分查找、双指针、滑动窗口)
文章目录
-
- 一、 数组理论基础
- 二、 二分查找
-
- 2.1 解题思路
- 2.2 练习题
-
- 2.2.1 二分查找(题704)
- 2.2.2 搜索插入位置(题35)
- 2.2.3 查找排序数组元素起止位置(题34)
- 2.2.4 有效的完全平方数(题367)
- 2.2.5 x 的平方根(题69)
- 2.2.6 寻找峰值(题162)
- 2.2.7 寻找旋转排序数组中的最小值(题153)
- 2.2.8 搜索旋转排序数组 (题33)
- 三 双指针法
-
- 3.1 解题思路
- 3.2 练习题
-
- 3.2.1 删除排序数组中的重复项(题26)
- 3.2.2 移动零(题283)
- 3.2.3 比较含退格的字符串(题844)
- 3.2.4 有序数组的平方(题977)
- 3.2.5 合并两个有序数组(题88)
- 3.2.6 两数之和 II - 输入有序数组(题167)
- 3.2.7 移动零(题283)
- 3.2.8 颜色分类(题75)
- 四、滑动窗口
-
- 4.1 解题思路
- 4.2 练习题
-
- 4.2.1 无重复字符的最长子串(题3)
- 4.2.2 字符串的排列(题567)
- 4.2.3 最小覆盖子串(题76)
- 4.2.4 最短超串
- 4.2.5 找到字符串中所有字母异位词(题438)
- 4.2.6 串联所有单词的子串(题30)
资源:力扣题库、LeetCode 刷题列表、代码随想录
一、 数组理论基础
参考代码随想录《数组理论基础》
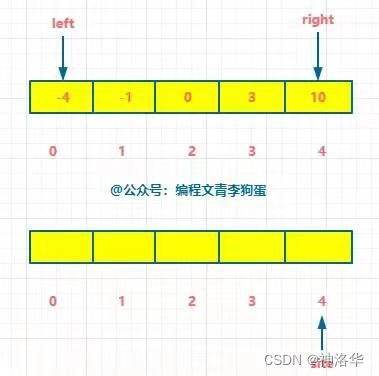
数组是存放在连续内存空间上的相同类型数据的集合,数组可以方便的通过下标索引的方式获取到下标下对应的数据,例如:

有两点需要注意:
- 数组下标都是从0开始的。
- 数组内存空间的地址是连续的
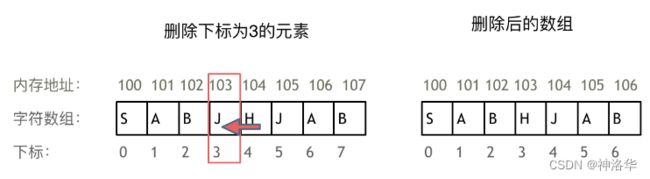
正是因为数组的在内存空间的地址是连续的,所以我们在删除或者增添元素的时候,就难免要移动其他元素的地址。例如删除下标为3的元素,需要对下标为3的元素后面的所有元素都要做移动操作,如图所示:
那么二维数组在内存的空间地址是连续的么?不同编程语言的内存管理是不一样的。在C++中二维数组是连续分布的,Java是没有指针的,同时也不对程序员暴露其元素的地址,寻址操作完全交给虚拟机。
二、 二分查找
2.1 解题思路
二分法的前提条件:数组为有序数组
循环不变量规则:在二分查找的过程中,区间的定义是不变量,所以在while寻找中每一次边界的处理都要坚持根据区间的定义来操作。
区间的定义决定了二分法的代码应该如何写。区间的定义一般为两种,左闭右闭即[left, right],或者左闭右开即[left, right)。
具体思路:
1. 左闭右闭写法
因为定义target在[left, right]区间,所以有如下两点:
while (left <= right)要使用<=,因为left == right是有意义的,所以使用 <=if (nums[middle] > target),right 要赋值为middle - 1,因为当前这个nums[middle]一定不是target,那么接下来要查找的左区间结束下标位置就是 middle - 1
2. 左闭右开写法
因为定义target在[left, right)区间,所以有如下两点:
while (left < right),这里使用 < ,因为left == right在区间[left, right)是没有意义的if (nums[middle] > target)right 更新为 middle,因为当前nums[middle]不等于target,去左区间继续寻找,而寻找区间是左闭右开区间,所以right更新为middle,即:下一个查询区间不会去比较nums[middle]
2.2 练习题
2.2.1 二分查找(题704)
解法一:左闭右闭:
class Solution:
def search(self, nums: List[int], target: int) -> int:
left, right = 0, len(nums) - 1 # 定义target在左闭右闭的区间里,[left, right]
while left <= right:
middle = left + (right - left) // 2 # 防止溢出 等同于(left + right)/2
if nums[middle] > target:
right = middle - 1 # target在左区间,所以[left, middle - 1]
elif nums[middle] < target:
left = middle + 1 # target在右区间,所以[middle + 1, right]
else:
return middle # 数组中找到目标值,直接返回下标
return -1 # 未找到目标值
解法二:左闭右开
class Solution:
def search(self, nums: List[int], target: int) -> int:
left, right = 0, len(nums) # 定义target在左闭右开的区间里,即:[left, right)
while left < right: # 因为left == right的时候,在[left, right)是无效的空间,所以使用 <
middle = left + (right - left) // 2
if nums[middle] > target:
right = middle # target 在左区间,在[left, middle)中
elif nums[middle] < target:
left = middle + 1 # target 在右区间,在[middle + 1, right)中
else:
return middle # 数组中找到目标值,直接返回下标
return -1 # 未找到目标值
2.2.2 搜索插入位置(题35)
要在数组中插入目标值,无非是这四种情况:
- 目标值在数组所有元素之前
- 目标值等于数组中某一个元素(就是上一题)
- 目标值插入数组中的位置
nums[pos−1] - 目标值在数组所有元素之后
对于数组中没有目标值的情况,其实就是寻找升序数组中第一个大于等于 target \textit{target} target 的下标。经过测试可知,这个下标是right+1(left),所以本题答案为:
class Solution(object):
def searchInsert(self, nums, target):
"""
:type nums: List[int]
:type target: int
:rtype: int
"""
left,right=0,len(nums)-1
ans=len(nums)
while left<=right:
mid=(left+right)//2
if nums[mid]<target:
left=mid+1
elif nums[mid]>target:
right=mid-1
else:
return mid
return right+1
2.2.3 查找排序数组元素起止位置(题34)
直观的思路肯定是从前往后遍历一遍。用两个变量记录第一次和最后一次遇见 target \textit{target} target 的下标,但这个方法的时间复杂度为 O ( n ) O(n) O(n),没有利用到数组升序排列的条件。由于数组已经排序,因此整个数组是单调递增的,我们可以利用二分法来加速查找的过程。
考虑target开始和结束位置,其实就是查找数组中第一个等于target 的位置(记为start)和第一个大于target 的位置减1(记为 end)。为了代码的复用,我们定义 lower_bound(nums,target)函数,表示在 n u m s nums nums 数组中二分查找 t a r g e t target target的位置。
最后,因为 t a r g e t target target可能不存在数组中,因此我们需要重新校验我们得到的两个下标,看是否符合条件,如果符合条件就返回[start,end],不符合就返回[−1,−1]。
class Solution(object):
def searchRange(self, nums, target):
"""
:type nums: List[int]
:type target: int
:rtype: List[int]
"""
def lower_bound(nums,target):
# lower_bound返回最小的满足nums[i]>=targrt的i
left,right=0,len(nums)-1
while left<=right:
mid=(left+right)//2
if nums[mid]<target:
left=mid+1
else:
right=mid-1
return right+1 # 或left
start=lower_bound(nums,target) # 第一个大于等于target的下标
if start==len(nums) or nums[start]!=target:
# 分别对应target大于整个数组和target不在数组中
return [-1,-1]
else:
end=lower_bound(nums,target+1)-1 # 第一个大于target 的下标
return [start,end]
2.2.4 有效的完全平方数(题367)
class Solution:
def isPerfectSquare(self, num: int) -> bool:
left,right=1,num
while left<=right:
mid=(left+right)//2
if mid*mid>num:
right=mid-1
elif mid*mid<num:
left=mid+1
else:
return True
return False
2.2.5 x 的平方根(题69)
由于 x 平方根的整数部分ans 是满足 k 2 ≤ x k^2 \leq x k2≤x的最大 k 值,因此我们可以对 k进行二分查找,从而得到答案。
二分查找的下界为 0,上界可以粗略地设定为 x。在二分查找的每一步中,我们只需要比较中间元素 mid 的平方与 x 的大小关系,并通过比较的结果调整上下界的范围。由于我们所有的运算都是整数运算,不会存在误差,因此在得到最终的答案 ans 后,也就不需要再去尝试 ans+1 了。
class Solution(object):
def mySqrt(self, x):
"""
:type x: int
:rtype: int
"""
left,right=0,x
while left<=right:
mid=(left+right)//2
if mid*mid<=x: # 根据牛顿迭代法,可以写mid**2<=x
left=mid+1
else:
right=mid-1
return right
2.2.6 寻找峰值(题162)
使用两个指针 left、right 。left 指向数组第一个元素,right 指向数组最后一个元素。取区间中间节点 mid,并比较 nums[mid] 和 nums[mid + 1] 的值大小。
- 如果 nums[mid] 小于 nums[mid + 1],则右侧存在峰值,令 left = mid + 1。
- 如果 nums[mid] 大于等于 nums[mid + 1],则左侧存在峰值,令 right = mid。
最后,当 left == right 时,跳出循环,返回 left。
class Solution(object):
def findPeakElement(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
left,right=0,len(nums)-1
while left<right:
mid = left + (right - left) // 2
if nums[mid] < nums[mid + 1]:
left = mid + 1
else:
right = mid
return left
2.2.7 寻找旋转排序数组中的最小值(题153)
二分查找的前提条件是数组有序,本题数组经过旋转之后,前半部分和后半部分也都是有序的,所以也可以使用二分查找。
数组经过「旋转」之后,会有两种情况,第一种就是原先的升序序列,另一种是两段升序的序列。第一种的最小值在最左边。第二种最小值在第二段升序序列的第一个元素。
- 如果
nums[mid] > nums[right],则最小值一定在 mid 右侧,则令left= mid + 1 ,继续查找右侧区间。
- 如果
nums[mid] ≤ nums[right],则最小值一定在 mid 左侧,或者 mid 位置,令 right = mid ,继续查找左侧区间。
class Solution(object):
def findMin(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
left,right=0,len(nums)-1
while left<right: # 不能取等号,保证查找区间至少有一个元素
mid=(left+right)//2
if nums[mid]>nums[right]:
left=mid+1
else:
right=mid
return nums[left]
类似题目还有154. 寻找旋转排序数组中的最小值 II ,代码如下:
class Solution:
def findMin(self, nums: List[int]) -> int:
left = 0
right = len(nums) - 1
while left < right:
mid = left + (right - left) // 2
if nums[mid] > nums[right]:
left = mid + 1
elif nums[mid] < nums[right]:
right = mid
else: # 无法判断在 mid 的哪一侧,可以采用 right = right - 1 逐步缩小区域
right = right - 1
return nums[left]
2.2.8 搜索旋转排序数组 (题33)
原本为升序排列的数组 nums 经过「旋转」之后,会有两种情况,第一种就是原先的升序序列,另一种是两段升序的序列。其实我们可以把第一种情况中的整个数组看做是左半部分,然后右半部分为空数组。所以将旋转后的数组看成左右两个升序部分:左半部分和右半部分。
创建两个指针 left、right,分别指向数组首尾。让后计算出两个指针中间值 mid。将 mid 与两个指针做比较,并考虑与 target 的关系。
-
如果 mid[mid] == target,说明找到了 target,直接返回下标。
-
如果 nums[mid] ≥ nums[left],则 mid 在左半部分(因为右半部分值都比 nums[left] 小)。
- 如果
nums[mid] ≥ target,并且 target ≥ nums[left],则 target 在左半部分,并且在 mid 左侧,此时应将 right 左移到 mid - 1 位置。
- 如果
nums[mid] ≤ target,则 target 在左半部分,并且在 mid 右侧,此时应将 left 右移到 mid + 1 位置。
- 如果
nums[left] > target,则 target 在右半部分,应将 left 移动到 mid + 1 位置。
-
如果 nums[mid] < nums[left],则 mid 在右半部分(因为右半部分值都比 nums[left] 小)。
- 如果
nums[mid] < target,并且 target ≤ nums[right],则 target 在右半部分,并且在 mid 右侧,此时应将 left 右移到 mid + 1 位置。
- 如果
nums[mid] ≥ target,则 target 在右半部分,并且在 mid 左侧,此时应将 right 左移到 mid - 1 位置。
- 如果
nums[right] < target,则 target 在左半部分,应将 right 左移到 mid - 1 位置
class Solution:
def search(self, nums: List[int], target: int) -> int:
left = 0
right = len(nums) - 1
while left <= right:
mid = left + (right - left) // 2
if nums[mid] == target:
return mid
if nums[mid] >= nums[left]:
if nums[mid] > target and target >= nums[left]:
right = mid - 1
else:
left = mid + 1
else:
if nums[mid] < target and target <= nums[right]:
left = mid + 1
else:
right = mid - 1
return -1
与之类似的还有搜索旋转排序数组 II,区别是数组元素会重复。
-
如果 nums[mid] > nums[left],则 mid 在左半部分(因为右半部分值都比 nums[left] 小)。
- 如果 nums[mid] ≥ target,并且 target ≥ nums[left],则 target 在左半部分,并且在 mid 左侧,此时应将 right 左移到 mid - 1 位置。
- 否则如果 nums[mid] < target,则 target 在左半部分,并且在 mid 右侧,此时应将 left 右移到 mid + 1。
- 否则如果 nums[left] > target,则 target 在右半部分,应将 left 移动到 mid + 1 位置。
-
如果 nums[mid] < nums[left],则 mid 在右半部分(因为右半部分值都比 nums[left] 小)。
- 如果 nums[mid] < target,并且 target ≤ nums[right],则 target 在右半部分,并且在 mid 右侧,此时应将 left 右移到 mid + 1 位置。
- 否则如果 nums[mid] ≥ target,则 target 在右半部分,并且在 mid 左侧,此时应将 right 左移到 mid - 1 位置。
- 否则如果 nums[right] < target,则 target 在左半部分,应将 right 左移到 mid - 1 位置。
-
最终判断 nums[left] 是否等于 target,如果等于,则返回 True,否则返回 False。
class Solution:
def search(self, nums: List[int], target: int) -> bool:
n = len(nums)
if n == 0:
return False
left = 0
right = len(nums) - 1
while left < right:
mid = left + (right - left) // 2
if nums[mid] > nums[left]:
if nums[left] <= target and target <= nums[mid]:
right = mid
else:
left = mid + 1
elif nums[mid] < nums[left]:
if nums[mid] < target and target <= nums[right]:
left = mid + 1
else:
right = mid
else:
if nums[mid] == target:
return True
else:
left = left + 1
return nums[left] == target
三 双指针法
3.1 解题思路
以 移除元素(27)举例,介绍双指针法。
- 暴力解法:这个题目暴力的解法就是两层for循环,一个for循环遍历数组元素 ,第二个for循环更新数组。删除过程如下:
很明显暴力解法的时间复杂度是 O ( n 2 ) O(n^2) O(n2),空间复杂度: O ( 1 ) O(1) O(1)。
- 双指针法(快慢指针法): 右指针
right 指向当前将要处理的元素,左指针left 指向下一个将要赋值的位置。通过一个快指针和慢指针在一个for循环下完成两个for循环的工作。
- 如果右指针指向的元素不等于
val,它一定是输出数组的一个元素,我们就将右指针指向的元素复制到左指针位置,然后将左右指针同时右移;
- 如果右指针指向的元素等于
val,它不能在输出数组里,此时左指针不动,右指针右移一位。
整个过程保持不变的性质是:区间[0,left) 中的元素都不等于 val。当左右指针遍历完输入数组以后,left 的值就是输出数组的长度。这样的算法在最坏情况下(输入数组中没有元素等于val),左右指针各遍历了数组一次。
class Solution:
def removeElement(self, nums: List[int], val: int) -> int:
fast = 0 # 快指针
slow = 0 # 慢指针
size = len(nums)
while fast < size: # a = size 时,nums[a] 会越界
"""
slow 用来收集不等于 val 的值,如果 fast 对应值不等于 val,
则把它与 slow 替换,同时slow+1。fast不管是否等于val,始终都有fast+1
"""
if nums[fast] != val:
nums[slow] = nums[fast]
slow += 1
fast += 1
return slow
- 双指针优化:
- 思路:如果要移除的元素恰好在数组的开头,例如序列 [1,2,3,4,5],当
val 为 1时,我们需要把每一个元素都左移一位。注意到题目中说:「元素的顺序可以改变」。实际上我们可以直接将最后一个元素 5 移动到序列开头,取代元素 1,得到序列 [5,2,3,4],同样满足题目要求。这个优化在序列中val 元素的数量较少时非常有效。
- 算法:实现方面,我们依然使用双指针,两个指针初始时分别位于数组的首尾,向中间移动遍历该序列。
如果左指针 left 指向的元素等于 val,此时将右指针right 指向的元素复制到左指针 left 的位置,然后右指针 right 左移一位。如果赋值过来的元素恰好也等于val,可以继续把右指针 right 指向的元素的值赋值过来(左指针left 指向的等于val 的元素的位置继续被覆盖),直到左指针指向的元素的值不等于 val 为止。
当左指针left 和右指针right 重合的时候,左右指针遍历完数组中所有的元素。
这样的方法两个指针在最坏的情况下合起来只遍历了数组一次。与方法一不同的是,方法二避免了需要保留的元素的重复赋值操作。
class Solution(object):
def removeElement(self, nums, val):
"""
:type nums: List[int]
:type val: int
:rtype: int
"""
slow,fast=0,len(nums)-1
while slow <=fast:
if nums[slow] ==val:
nums[slow]=nums[fast]
fast-=1
else:
slow+=1
return slow
3.2 练习题
3.2.1 删除排序数组中的重复项(题26)
class Solution(object):
def removeDuplicates(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
fast = 1 # 快指针,因为后面会用到fast-1,所以fast赋值从1开始
slow = 1 # 慢指针
size = len(nums)
while fast < size: # a = size 时,nums[a] 会越界
if nums[fast] != nums[fast-1]: # 判断很前一个数是否重复
nums[slow] = nums[fast]
slow += 1
fast += 1
return slow
3.2.2 移动零(题283)
思路:使非0元素左移,等同于使0往右移。
算法:使用双指针,右指针不断向右移动。每次右指针指向非零数,则将左右指针对应的数交换,同时左指针右移,否则只有右指针右移,左指针不动。
每次交换,都是将左指针的零与右指针的非零数交换,结果就是左右指针之间都是0。
class Solution(object):
def moveZeroes(self, nums):
"""
:type nums: List[int]
:rtype: None Do not return anything, modify nums in-place instead.
"""
left,right = 0,0
while right < len(nums): # a = size 时,nums[a] 会越界
if nums[right] != 0:
nums[left],nums[right] = nums[right], nums[left]
left+= 1
right+=1
return nums
也可以看做是参考了快速排序的思想,用0当做这个中间点,把不等于0(注意题目没说不能有负数)的放到中间点的左边,等于0的放到其右边。使用两个指针left和right,只要nums[right]!=0,我们就交换nums[left]和nums[right]:
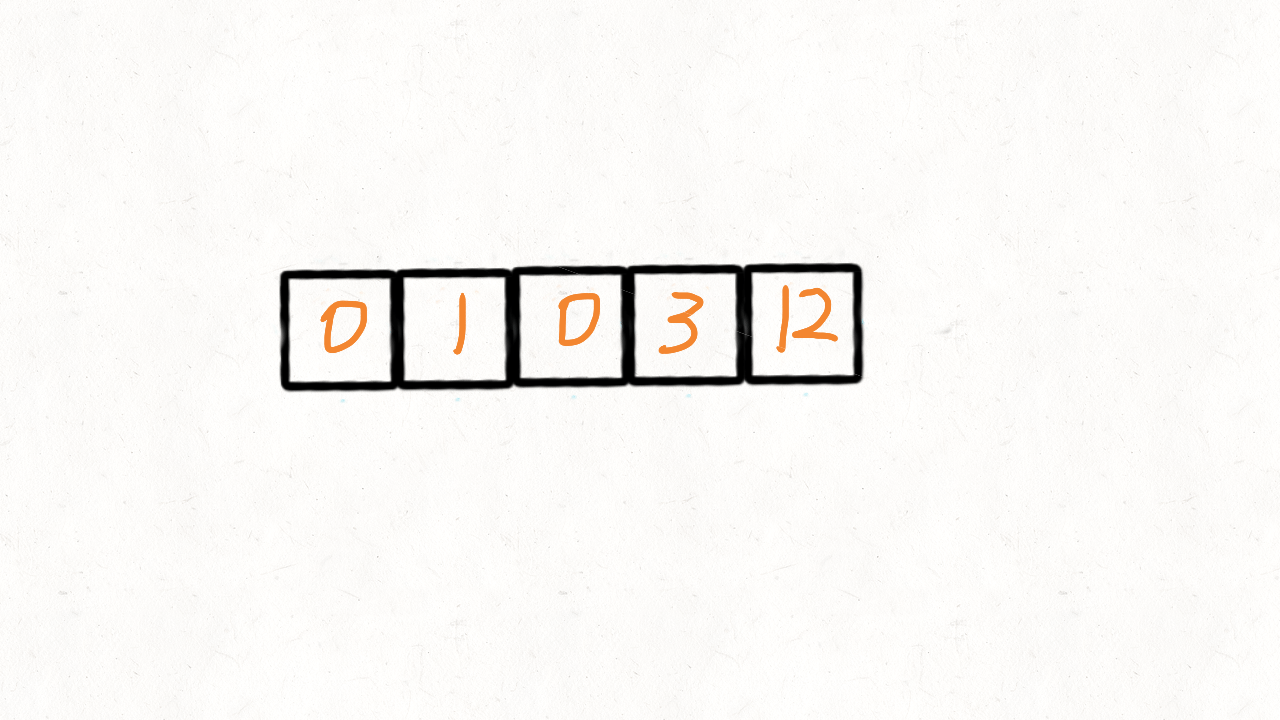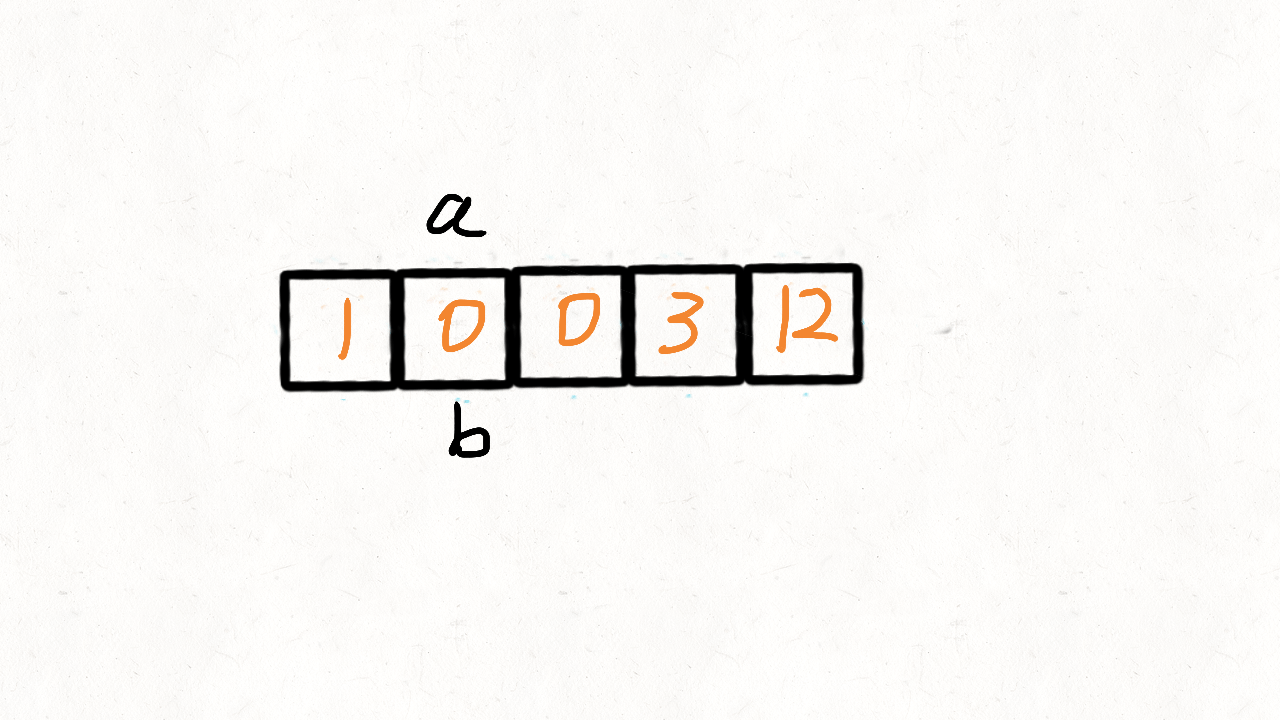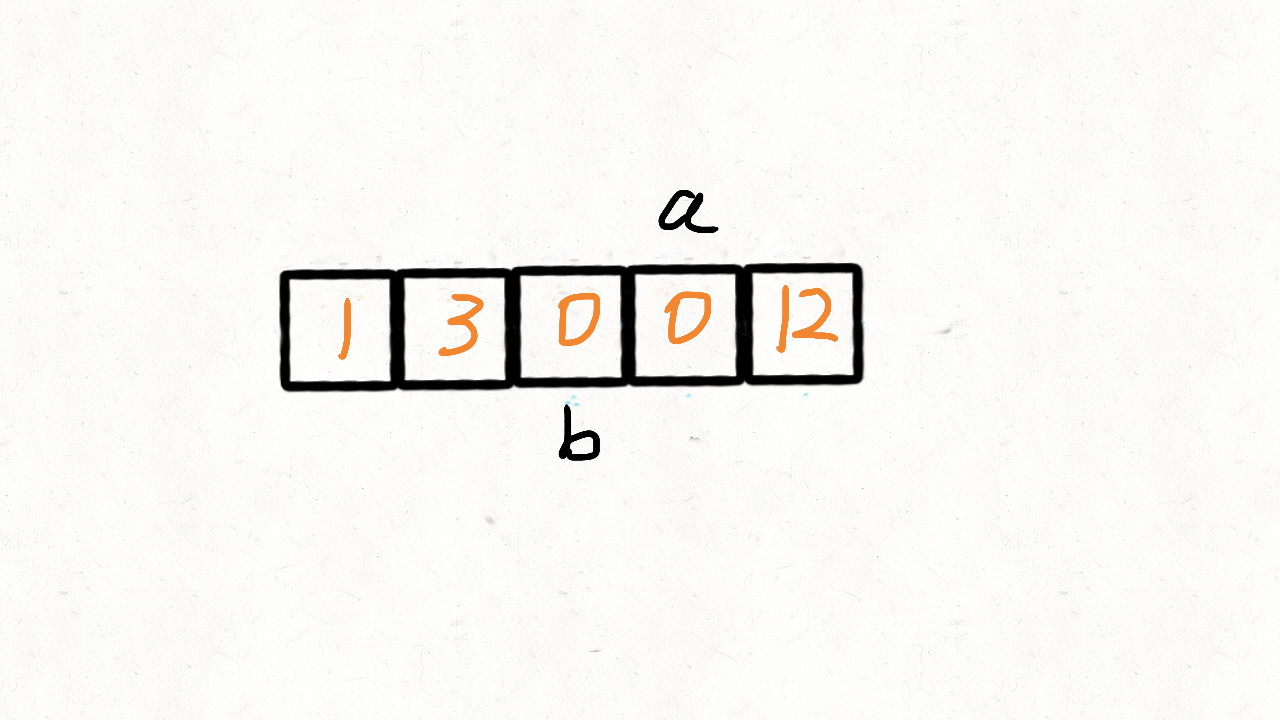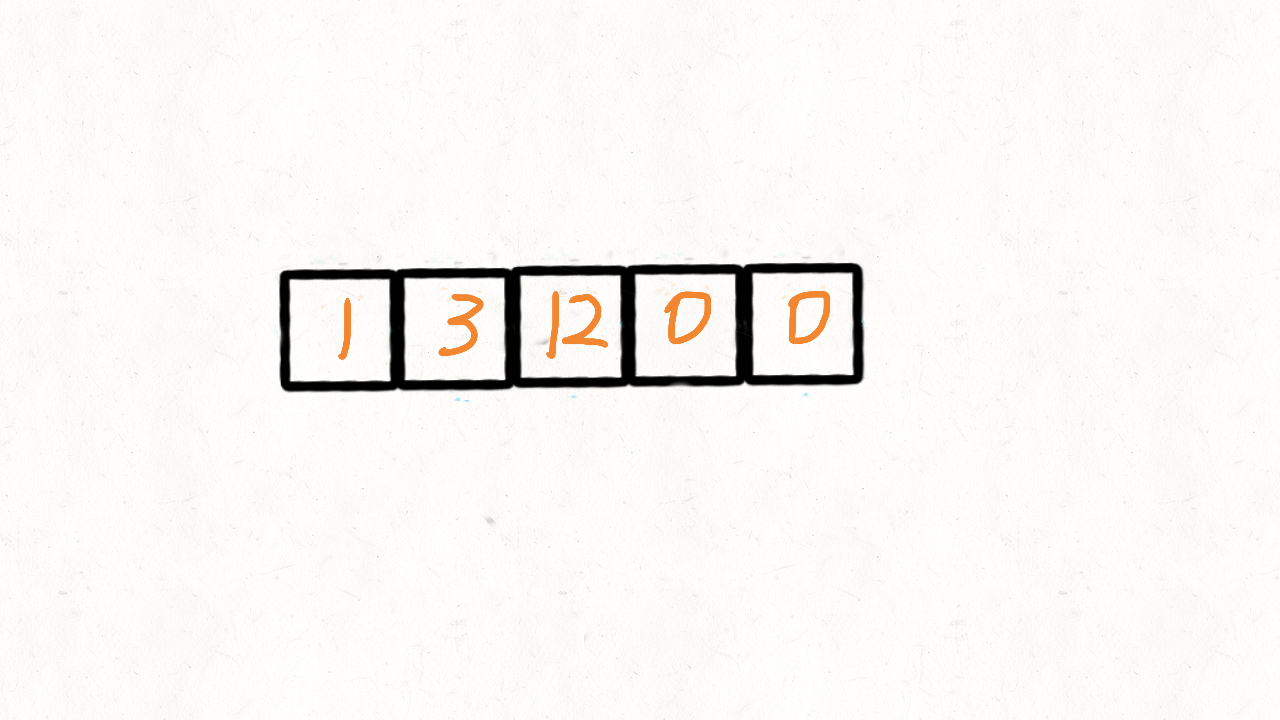
用for循环写出来就是:
class Solution(object):
def moveZeroes(self, nums):
"""
:type nums: List[int]
:rtype: None Do not return anything, modify nums in-place instead.
"""
left = 0
for right in range(len(nums)):
# 当前元素!=0,就把其交换到左边,等于0的交换到右边
if nums[right]:
nums[left],nums[right] = nums[right],nums[left]
left += 1
如果right指针指向末尾来进行交换,会改变非0元素顺序。
3.2.3 比较含退格的字符串(题844)
栈有后进先出的特性,比如网页的后退、文本编辑中的撤销操作等,这些操作的特性都契合这个特性,本题也是一样,所以可以考虑用栈来处理。
方法一:重构字符串:用栈处理遍历过程,每次我们遍历到一个字符:
- 如果它是退格符,那么我们将栈顶弹出;
- 如果它是普通字符,那么我们将其压入栈中。
class Solution(object):
def backspaceCompare(self, s, t):
"""
:type s: str
:type t: str
:rtype: bool
"""
def build(s):
ls = list()
for ch in s:
if ch != "#":
ls.append(ch)
elif ls:
ls.pop()
return "".join(ls)
return build(s) == build(t)
复杂度分析
- 时间复杂度: O ( N + M ) O(N+M) O(N+M),其中 N 和 M分别为字符串 S 和 T 的长度。我们需要遍历两字符串各一次。
- 空间复杂度: O ( N + M ) O(N+M) O(N+M),其中 N 和 M 分别为字符串 S 和 T 的长度。主要为还原出的字符串的开销。
方法二:双指针
class Solution(object):
def backspaceCompare(self, s, t):
"""
:type s: str
:type t: str
:rtype: bool
"""
def back(s):
s=list(s)
slow,fast=0,0
while fast<len(s):
# 只要快指针不是指向'#'就将其赋值给慢指针,同时慢指针右移
if s[fast]!="#":
s[slow]=s[fast]
slow+=1
else: # 当快指针指向'#'时慢指针后退一格
if slow>0: # 慢指针指向空不再退格
slow-=1
fast+=1
return s[:slow]
return back(s)==back(t)
方法三:双指针(官方)
一个字符是否会被删掉,只取决于该字符后面的退格符,而与该字符前面的退格符无关。因此当我们逆序地遍历字符串,就可以立即确定当前字符是否会被删掉。
具体地,我们定义skip 表示当前待删除的字符的数量。每次我们遍历到一个字符:
- 若该字符为退格符,则我们需要多删除一个普通字符,我们让
skip + 1;
- 若该字符为普通字符:
- 若
skip 为 0,则说明当前字符不需要删去;
- 若
skip 不为 0,则说明当前字符需要删去,我们让skip - 1。
所以可以定义两个指针,分别指向两字符串的末尾。每次我们让两指针逆序地遍历两字符串,直到两字符串能够各自确定一个字符,然后将这两个字符进行比较。重复这一过程直到找到的两个字符不相等,或遍历完字符串为止。
class Solution(object):
def backspaceCompare(self, s, t):
"""
:type s: str
:type t: str
:rtype: bool
"""
up,down=len(s)-1,len(t)-1
skip_s,skip_t=0,0
while up>=0 or down>=0: #同时遍历两个字符串
while up>=0: # 先逆序遍历s中字符串,找到不需要删除的普通字符
if s[up]=='#':
skip_s+=1
up-=1
else:
if skip_s>0:
up-=1
skip_s-=1
else:
break
while down>=0: # 先逆序遍历s中字符串,找到不需要删除的普通字符
if t[down]=='#':
skip_t+=1
down-=1
else:
if skip_t>0:
down-=1
skip_t-=1
else:
break
# 开始进行字符对比
if up>=0 and down>=0:
if s[up]!=t[down]:
return False
# 存在一个字符串遍历完而另一个还没遍历完的情况,此时也是返回False
elif up>=0 or down>=0:
return False
# 无论何种情况都要开始遍历到下一个位置
up-=1
down-=1
return True
3.2.4 有序数组的平方(题977)
本题主要思路是原数组nuns本身是有序的,只不过负数的平方反过来成了降序。比如[-3,-2,-1]是升序的,其平方[9,4,1]成了降序。这样造成数组每个元素平方之后,是一个两边大中间小的结构:
输入:nums = [-4,-1,0,3,10]
平方:nums =[16,1,0,9,100]
此时可以考虑使用一个额外的列表ls,初始化为与nums等长。然后使用指针idx从后往前遍历ls,则每次最大的元素一定是从nums的两端往中间取,至于具体是左端还是右端,比较这两个元素就行。故考虑使用左右指针left和right,分别从0和-1的位置开始遍历。具体的:
- 若
nums[left]**2<=nums[right]**2,则ls[idx]=nums[right]**2,同时左指针往右一格遍历nums左侧的下一个元素
- 若
nums[left]**2>nums[right]**2,则ls[idx]=nums[left]**2,同时右指针往左一格遍历nums右侧的下一个元素
- 每次ls赋值完,指针
idx都左移一格,即idx-=1。
参考别人图解则是:
class Solution(object):
def sortedSquares(self, nums):
"""
:type nums: List[int]
:rtype: List[int]
"""
# 初始化额外数组ls,初始赋值nums左右指针和数组ls的末端指针idx
ls=[-1]*len(nums)
left,right,idx=0,len(nums)-1,len(nums)-1
# 开始从末端遍历ls,最大值只会来自nums的两端,故遍历左右指针,更大的数赋值给ls[idx]
while left <=right:
if nums[left]**2<=nums[right]**2:
ls[idx]=nums[right]**2
# 右侧更大则赋值给ls[idx],同时right和idx都右移一位
right-=1
idx-=1
else:
ls[idx]=nums[left]**2
left+=1
idx-=1
return ls
3.2.5 合并两个有序数组(题88)
给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2,其元素个数分别是 m 和 n 。请你 合并 nums2 到 nums1 中,使合并后的数组同样按 非递减顺序 排列。
注意:最终,合并后数组不应由函数返回,而是存储在数组 nums1 中。为了应对这种情况,nums1 的初始长度为 m + n,其中前 m 个元素表示应合并的元素,后 n 个元素为 0 ,应忽略。nums2 的长度为 n 。
示例 :
- 输入:nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3
- 输出:[1,2,2,3,5,6]
- 解释:需要合并 [1,2,3] 和 [2,5,6] 。
- 合并结果是 [1,2,2,3,5,6] ,其中斜体加粗标注的为 nums1 中的元素。
- nums1.length == m + n,0 <= m, n <= 200
这道题和上一题很相似,两个数组都是有序的,为了利用这一性质,我们可以使用双指针方法,每次将两个数组中更大的元素放在nums1末尾。这样做是为了不使用额外的存储空间,所以需要倒序遍历。
class Solution(object):
def merge(self, nums1, m, nums2, n):
"""
:type nums1: List[int]
:type m: int
:type nums2: List[int]
:type n: int
:rtype: None Do not return anything, modify nums1 in-place instead.
"""
# p1和p2分别指向两个数组的末尾,倒序遍历
p1,p2=m-1,n-1
idx=m+n-1
# p1、p2如果不限制可以为负值,也能表示下标,所以不能单纯设置idx》0
while p1>=0 and p2>=0:
# print(p1,p2,idx)
if nums1[p1]>nums2[p2]:
# 这里写nums1[idx]=nums1[p1]结果也正确,下同
nums1[idx],nums1[p1]=nums1[p1],nums1[idx]
p1-=1
else:
nums1[idx],nums2[p2]=nums2[p2],nums1[idx]
p2-=1
idx-=1
# 当nums1序列中大数排完后,p1=0,循环终止,此时p2可能还有剩下的数,这些数都是最小的一部分,直接接到nums1前面
# print(nums2[:p2+1] )
nums1[:p2+1]=nums2[:p2+1]
return nums1
3.2.6 两数之和 II - 输入有序数组(题167)
这道题和两数之和(题3)的区别是,数组是有序的。所以可以考虑使用两个指针分别遍历数组,如果两个元素之和小于目标值,则将左侧指针右移一位。如果两个元素之和大于目标值,则将右侧指针左移一位。重复上述操作,直到找到答案。
class Solution:
def twoSum(self, numbers: List[int], target: int) -> List[int]:
low, high = 0, len(numbers) - 1
while low < high:
total = numbers[low] + numbers[high]
if total == target:
return [low + 1, high + 1]
elif total < target:
low += 1
else:
high -= 1
return [-1, -1]
3.2.7 移动零(题283)
class Solution(object):
def moveZeroes(self, nums):
"""
:type nums: List[int]
:rtype: None Do not return anything, modify nums in-place instead.
"""
left = 0 # 两个指针l和r
for right in range(len(nums)):
# 当前元素!=0,就把其交换到左边,等于0的交换到右边
if nums[right]:
nums[left],nums[right] = nums[right],nums[left]
left += 1
3.2.8 颜色分类(题75)
方法一:单指针
这道题和上一题很类似,最简单的方法是遍历两次,先将0排到最前面,再接着将1排到前面:
class Solution:
def sortColors(self, nums: List[int]) -> None:
"""
Do not return anything, modify nums in-place instead.
"""
# 两次遍历,先排0再排1
left=0
for i in range(len(nums)):
if nums[i]==0:
nums[left],nums[i]=nums[i],nums[left]
left+=1
right=left # 前面left个位置已经排好了0
for j in range(right,len(nums)):
if nums[j]==1:
nums[right],nums[j]=nums[j],nums[right]
right+=1
return nums
方法二:双指针(官方题解)
我们可以额外使用一个指针,即使用两个指针分别用来交换 0 和1。具体地,我们用指针 p 0 p_0 p0来交换 0, p 1 p_1 p1来交换 1,初始值都为 0。当我们从左向右遍历整个数组时:
- 如果找到了 1,那么将其与 n u m s [ p 1 ] nums[p_1] nums[p1] 进行交换,并将 p 1 p_1 p1向后移动一个位置,这与方法一是相同的;
- 如果找到了 0,那么将其与 n u m s [ p 0 ] nums[p_0] nums[p0] 进行交换,并将 p 0 p_0 p0向后移动一个位置。这样做是正确的吗?
我们可以注意到,因为连续的 0 之后是连续的 1,因此如果我们将 0 与 n u m s [ p 0 ] nums[p_0] nums[p0] 进行交换,那么我们可能会把一个 1 交换出去。当 p 0 < p 1 p_0 < p_1 p0<p1时,我们已经将一些 1 连续地放在头部,此时一定会把一个 1 交换出去,导致答案错误。因此,如果 p 0 < p 1 p_0 < p_1 p0<p1,那么我们需要再将 n u m s [ i ] nums[i] nums[i] 与 n u m s [ p 1 ] nums[p_1] nums[p1]进行交换,其中 i 是当前遍历到的位置。
在进行了第一次交换后, n u m s [ i ] nums[i] nums[i]的值为 1,我们需要将这个 1 放到「头部」的末端。在最后,无论是否有 p 0 < p 1 p_0 < p_1 p0<p1,我们需要将 p 0 p_0 p0 和 p 1 p_1 p1均向后移动一个位置,而不是仅将 p 0 p_0 p0向后移动一个位置。
class Solution:
def sortColors(self, nums: List[int]) -> None:
"""
Do not return anything, modify nums in-place instead.
"""
# 两个指针分别用于交换0和1
p0=p1=0
for i in range(len(nums)):
if nums[i]==1:
nums[i],nums[p1]=nums[p1],nums[i]
p1+=1
elif nums[i]==0:
nums[i],nums[p0]=nums[p0],nums[i]
if p0<p1:
nums[i],nums[p1]=nums[p1],nums[i]
p1+=1
p0+=1
return nums
方法三:快速排序
我们也可以借鉴快速排序算法中的 partition 过程,将 1 作为基准数 pivot,然后将序列分为三部分:0(即比 1 小的部分)、等于 1 的部分、2(即比 1 大的部分)。具体步骤如下:
- 使用两个指针 left、right,分别指向数组的头尾。left 表示当前处理好红色元素的尾部,right 表示当前处理好蓝色的头部。
- 再使用一个下标 index 遍历数组,如果遇到
nums[index] == 0,就交换 nums[index] 和 nums[left],同时将 left 右移。如果遇到 nums[index] == 2,就交换 nums[index] 和 nums[right],同时将 right 左移。
- 直到 index 移动到 right 位置之后,停止遍历。遍历结束之后,此时 left 左侧都是红色,right 右侧都是蓝色。
- 注意:移动的时候需要判断 index 和 left 的位置,因为 left 左侧是已经处理好的数组,所以需要判断 index 的位置是否小于 left,小于的话,需要更新 index 位置。
class Solution:
def sortColors(self, nums: List[int]) -> None:
left = 0
right = len(nums) - 1
index = 0
while index <= right:
if index < left:
index += 1
elif nums[index] == 0:
nums[index], nums[left] = nums[left], nums[index]
left += 1
elif nums[index] == 2:
nums[index], nums[right] = nums[right], nums[index]
right -= 1
else:
index += 1
四、滑动窗口
4.1 解题思路
下面以长度最小的子数组(题209)这一题讲解滑动窗口的思路。
给定一个含有 n 个正整数的数组nums和一个正整数 target 。找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, …, numsr-1, numsr] ,并返回其长度。如果不存在符合条件的子数组,返回 0 。
- 示例1:
- 输入:s = 7, nums = [2,3,1,2,4,3] 输出:2 解释:子数组 [4,3] 是该条件下的长度最小的子数组。
- 输出:2
- 解释:子数组 [4,3] 是该条件下的长度最小的子数组。
- 示例2:
- 输入:target = 11, nums = [1,1,1,1,1,1,1,1]
- 输出:0
解法一:暴力解法
使用两个for循环,然后不断的寻找符合条件的子序列,时间复杂度很明显是 O ( n 2 ) O(n^2) O(n2)。
具体的,先初始化子数组的最小长度为无穷大,枚举数组nums 中的每个下标作为子数组的开始下标,对于每个开始下标 i,需要找到大于或等于 i 的最小下标 j,使得从 [nums[i] , nums[j] ]的元素和大于或等于 s,并更新子数组的最小长度(此时子数组的长度是 j−i+1)。
class Solution:
def minSubArrayLen(self, s: int, nums: List[int]) -> int:
if not nums:
return 0
n = len(nums)
ans = n + 1 # 存储最小数组长度
for i in range(n):
total = 0
for j in range(i, n): # 计算位置i到位置j的元素和
total += nums[j]
if total >= s:
ans = min(ans, j - i + 1)
break
return 0 if ans == n + 1 else ans
解法二:滑动窗口

思路:使用一个动态区间,维护整个区间的和都是大于等于target,从左往右遍历并不断更新动态区间的长度。以题目中的示例来举例,target = 7, nums = [2,3,1,2,4,3]来看一下查找的过程:
其实从动画中可以发现滑动窗口也可以理解为双指针法的一种!只不过这种解法更像是一个窗口的移动,所以叫做滑动窗口更适合一些。
在本题中实现滑动窗口,主要确定如下三点:
- 窗口内是什么?:满足其和 ≥ s 的长度最小的 连续 子数组。
- 如何移动窗口的起始位置?:如果当前窗口的值大于s了,窗口就要向前移动了
- 如何移动窗口的结束位置?:窗口的结束位置就是遍历数组的指针
具体的,将右指针right遍历到数组的最右端,遍历过程中,求出当前子数组的和(使用一个变量total来维护)。在total >= target时,我们就缩小区间,即左指针移右移,此时需要total-nums[left]更新区间和,并更新区间长度ans。然后 右指针继续右移,这样我们总是保证了total >= target。 最终右指针右移到数组末尾依旧没找到total >= target,或者找到最短子数组长度ans。
注意,只有total >= target时,左指针才会移动。因此,当右指针移动到下一个位置时,总是有前缀和total >= s。可以看作是,每次左指针移动都是在找到一个新的更短的符合条件的连续子数组,因此维护的总和total一定是>=s的,而答案一定是更新的。
class Solution(object):
def minSubArrayLen(self, target, nums):
if len(nums)==0:
return 0
else:
n = len(nums)
# 初始化左右指针、区间和以及区间长度
left, right = 0, 0
total = 0
ans = n + 1
# 移动右指针,计算当前子数组的和
while right < n:
total += nums[right]
# 只要和大于目标值,左指针就一直右移
while total >= target:
ans = min(ans, right - left + 1) # 先更新区间长度再移动指针
total -= nums[left] # 区间和减去刚刚舍去的左指针的值
left += 1
right += 1
return 0 if ans == n + 1 else ans
滑动窗口的精妙之处在于根据当前子序列和大小的情况,不断调节子序列的起始位置。从而将 O ( n 2 ) O(n^2) O(n2)暴力解法降为 O ( n ) O(n) O(n)。
4.2 练习题
4.2.1 无重复字符的最长子串(题3)
给定一个字符串 s ,请你找出其中不含有重复字符的 最长子串 的长度。
- 输入: s = “abcabcbb”
- 输出: 3
- 解释: 因为无重复字符的最长子串是 “abc”,所以其长度为 3。
方法一:官方解法
使用两个指针表示最长子串的左右边界,依次递增地枚举子串的起始位置left。假设left=k,我们得到了不含重复字符的最长子串的结束位置为right。那么下一次遍历到left=k+1时,k+1到right这个区间字符串仍是不重复的。由于left左移,区间缩小,故right应该右移遍历,直到右侧出现了重复字符为止。
在上面的流程中,我们还需要使用一种数据结构来判断是否有重复的字符,可以直接使用集合。在左指针右移动的时候,我们从集合中移除一个字符;在右指针向右移动的时候,我们往集合中添加一个字符。
class Solution:
def lengthOfLongestSubstring(self, s: str) -> int:
# 哈希集合,记录每个字符是否出现过
se = set()
# 右指针,初始值为 -1,相当于我们在字符串的左边界的左侧,还没有开始移动
right, ans = -1, 0
for i in range(len(s):
if i != 0: # 从第二个字符开始删除
# 左指针向右移动一格,移除一个字符
se.remove(s[i - 1])
while right + 1 < len(nums) and s[right + 1] not in se:
# 不断地移动右指针
se.add(s[right + 1])
right += 1
# 第 i 到 rk 个字符是一个极长的无重复字符子串
ans = max(ans, right - i + 1)
return ans
方法二:滑动窗口
class Solution(object):
def lengthOfLongestSubstring(self, s):
"""
:type s: str
:rtype: int
"""
left,right=0,0
# 因为重复的元素会出现在任何位置,比如'abccd',不能简单的用列表pop(0)
# 和位置无关的位置结构,可以选用集合
se=set()
ans=0 # 子串长度初始化为0,当s为空时,不会进入for循环,此时长度依旧为0
for right in range(len(s)):
# 指针右移,首先添加第一个元素
while s[right] in se:
# 当右指针遇到重复元素时,左指针右移,当前长度减一
# 直到右指针不再和集合中元素重复
se.remove(s[left])
left+=1
ans=max(ans,right-left+1)
se.add(s[right])
return ans
注意:应该将se.add(s[right]) 放在 while 循环之后,否则每次集合先添加,就肯定可以进while循环了。
方法三:
class Solution(object):
def lengthOfLongestSubstring(self, s):
"""
:type s: str
:rtype: int
"""
# 定义当前最长不重复子串的长度
le = 0
# 定义字典,用于记录每个字符最后一次出现的位置
d = {}
# 定义left指针,用于维护当前子串
left = -1
for r in range(len(s)):
if s[r] in d: # 如果当前字符已经在字典中出现过
left = max(left, d[s[r]]) # 更新left指针位置
d[s[r]] = r # 更新当前字符最后一次出现的位置
# 更新最长不重复子串的长度
le = max(le, r - left)
return le
上面代码中,首先定义了当前最长不重复子串的长度 le,用于记录结果;字典 d,用于记录每个字符最后一次出现的位置;left指针,用于维护当前子串。
接下来使用for循环遍历字符串s,对于每个字符,如果当前字符已经在字典中出现过,那么left指针应该跳到该字符上一次出现的位置的后面一个位置,这样才能保证当前子串中没有重复字符。然后更新当前字符最后一次出现的位置,遍历right指针并更新答案即可。
需要注意的是,重复字符上一次出现的位置可能会更小(比如’abbac’),故需要设置为max(left, d[s[r]])。
4.2.2 字符串的排列(题567)
给你两个字符串 s1 和 s2 ,写一个函数来判断 s2 是否包含 s1 的排列。如果是,返回 true ;否则,返回 false 。换句话说,s1 的排列之一是 s2 的 子串 。
- 输入:s1 = “ab” s2 = “eidbaooo”
- 输出:true
- 解释:s2 包含 s1 的排列之一 (“ba”).
这道题是 76. 最小覆盖子串 的简单版本。解题思路:滑动窗口 + 字典
-
分析一: 题目要求 s1 的排列之一是 s2 的一个子串。而子串必须是连续的,所以要求的 s2 子串的长度跟 s1 长度必须相等。
-
分析二: 那么我们有必要把 s1 的每个排列都求出来吗?当然不用。如果字符串 a 是 b 的一个排列,那么当且仅当它们两者中的每个字符的个数都必须完全相等。
所以,根据上面两点分析,我们已经能确定这个题目可以使用 滑动窗口 + 字典 来解决。
我们使用一个长度和 s1 长度相等的固定窗口大小的滑动窗口,在 s2 上面从左向右滑动,判断 s2 在滑动窗口内的每个字符出现的个数是否跟 s1 每个字符出现次数完全相等。
我们定义 counter1 是对 s1 内字符出现的个数的统计,定义 counter2 是对 s2 内字符出现的个数的统计。在窗口每次右移的时候,需要把右边新加入窗口的字符个数在 counter2 中加 1,把左边移出窗口的字符的个数减 1。 if counter1 == counter2 ,那么说明窗口内的子串是 s1 的一个排列,返回 True;如果窗口已经把 s2 遍历完了仍然没有找到满足条件的排列,返回 False。
对于题目给的示例一:s1 = “ab” s2 = “eidbaooo”,我制作了滑动窗口过程的动画帮助理解:
gif动图裁剪压缩网站
躲坑指南:
- 本题中的
counter 可以用字典,也可以用数组来实现。用字典的时候,需要注意:如果移除 left 元素后,若 counter2[s2[left]] == 0 那么需要从字典中删除 s2[left] 这个key。因为 {"a":0, "b":1} 和 {"b":1} 是不等的。
- 窗口的定义一定要搞清楚是否包含两边的端点,比如我定义的窗口是
[left, right] 两个端点都包含,那么就需要把两个端点的元素也放入 counter2 中。
counter2 初始化的时候只放了 [0, right - 1] 个元素,因为在 while 循环中的第一行就是把 right 元素放到 counter2 中。
class Solution(object):
def checkInclusion(self, s1, s2):
"""
:type s1: str
:type s2: str
:rtype: bool
"""
# 统计 s1 中每个字符出现的次数
counter1 = collections.Counter(s1)
N = len(s2)
# 定义滑动窗口的范围是 [left, right],闭区间,长度与s1相等
left ,right = 0,len(s1) - 1
# 统计窗口s2[left, right - 1]内的元素出现的次数
counter2 = collections.Counter(s2[0:right])
while right < N:
# 把 right 位置的元素放到 counter2 中
counter2[s2[right]] += 1
# 如果滑动窗口内各个元素出现的次数跟 s1 的元素出现次数完全一致,返回 True
if counter1 == counter2:
return True
# 窗口向右移动前,把当前 left 位置的元素出现次数 - 1
counter2[s2[left]] -= 1
# 如果当前 left 位置的元素出现次数为 0, 需要从字典中删除,否则这个出现次数为 0 的元素会影响两 counter 之间的比较
if counter2[s2[left]] == 0:
del counter2[s2[left]]
# 窗口向右移动
left += 1
right += 1
return False
写法二:(『 一招吃遍七道 』滑动窗口的应用)
在窗口滑动的过程中,我们维持一个长度为 len(s1) 的滑动窗口,当窗口中待匹配的字符数目为 0,我们就找到了一个满足要求的子串。此题更进一步的思路可以看下一题最小覆盖子串(题76)的解答。
class Solution:
def checkInclusion(self, s1: str, s2: str) -> bool:
if len(s1)>len(s2):
return False
else:
from collections import Counter
count1=dict(Counter(s1))
need=len(s1) #所需字符的总次数
for right in range(len(s2)):
ch=s2[right]
"""
如果ch是所需的字符,就将ch需要的次数减一,
但是ch次数>0时,才表示这个字符还需要,此时才有need+1
而且要先计算need次数,因为ch次数先操作会导致need统计错误,类似于计算窗口的值再移动窗口
"""
if ch in count1:
if count1[ch]>0:
need-=1
count1[ch]-=1
"""
窗口是固定大小,左指针跟随右指针移动,同时维护需求字典
一开始窗口还不到s1长度,此时left会小于0。left=0是窗口第一次右移
"""
left=right-len(s1)
if left>=0:
ch=s2[left]
if ch in count1:
if count1[ch]>=0:
need+=1
count1[ch]+=1
if need==0:
return True
return False
4.2.3 最小覆盖子串(题76)
这道题和剑指 Offer II 017. 含有所有字符的最短字符串几乎是一样的,区别仅仅在于本题的最短子串只有唯一一个,而后者可能出现多个,只要求取其中任意一个就行。所以二者的代码可以是完全一样的。
我们以哈希表cnt记录目标字符串 t 中待匹配的各字符的数目,并在 s 中维护一个变长的滑动窗口,期望使得窗口中的字符能够覆盖 t。具体地,设定一个非负变量 need 表示当前窗口还需要匹配到的字符总数:
-
当窗口新增一位字符 ch 时:
- 若
cnt[ch]>0,说明 待加入的字符ch 是当前窗口还需要的,此时新加入的 ch 能够使得 need-1
- 若
cnt[ch]≤0,说明 当前窗口不需要这个字符,need不变
- 无论
cnt[ch]是否大于0,由于窗口一直右移,cnt[ch]本身的次数是要减一的。所以cnt[ch] 可以为负值,这表示表示当前窗口中字符 ch 过多。
-
当窗口滑出一位字符 ch 时:
- 若
cnt[ch]≥0,说明 待加入的字符ch 是当前窗口还需要的(滑出去需求更大了),此时滑出的 ch 能够使得 need+1
- 若
cnt[ch]<0,说明 当前窗口不需要这个字符,need不变
- 无论
cnt[ch]是否大于0,由于窗口一直右移,cnt[ch]本身的次数是要加一的。
-
当 need=0 时,说明找到了覆盖子串 ,在记录下答案的同时,我们还需要尝试收缩窗口左边界(参照上一步)。
class Solution:
def minWindow(self, s: str, t: str) -> str:
if len(t)>len(s):
return ""
elif s==t:
return s
else:
from collections import Counter
cnt=dict(Counter(t)) # 哈希表:记录需要匹配到的各个字符的数目
left=0
need=len(t) # 需匹配的字符总数。每次右指针匹配到所需字符,need-=1,所以need=0表示匹配到了完整的覆盖子串
le=len(s)+1 # 最短长度
result="" # 覆盖子串,即返回的结果
for right in range(len(s)):
ch=s[right]
if ch in cnt: # 窗口右端新加入的字符ch若位于s1中,就将其次数-1。可以是负数,表示ch有多余的
if cnt[ch]>0: # 但是只有字符ch大于0,才表示这个字符还需要,need-=1
need-=1
cnt[ch]-=1
while need==0: # 只要所需字符为0,就一直移动左指针
ch=s[left]
if ch in cnt: # 刚滑出的字符位于s1中,操作同上
if cnt[ch]>=0:
need+=1
cnt[ch]+=1
# 下面这一段写在while语句之前也可以,只要left+=1在最后一行
if right-left<le:
le=right-left
result=s[left:right+1]
left+=1
return "" if le==len(s)+1 else result
4.2.4 最短超串
题目链接
这题和上一题差不多,改一下输出结果的格式就行。
class Solution(object):
def shortestSeq(self, big, small):
"""
:type big: List[int]
:type small: List[int]
:rtype: List[int]
"""
from collections import Counter
cnt=dict(Counter(small)) # 哈希表:记录需要匹配到的各个字符的数目
left=0
need=len(small) # 需匹配的字符总数。每次右指针匹配到所需字符,need-=1,所以need=0表示匹配到了完整的覆盖子串
le=len(big)+1 # 记录最短子串长度
result=[] # 返回的结果
for right in range(len(big)):
ch=big[right]
if ch in cnt: # 窗口右端新加入的字符ch若位于s1中,就将其次数-1。可以是负数,表示ch有多余的
if cnt[ch]>0: # 但是只有字符ch大于0,才表示这个字符还需要,need-=1
need-=1
cnt[ch]-=1
while need==0: # 只要所需字符为0,就一直移动左指针
ch=big[left]
if ch in cnt: # 刚滑出的字符位于s1中,操作同上
if cnt[ch]>=0:
need+=1
cnt[ch]+=1
# 下面这一段写在while语句之前也可以,只要left+=1在最后一行
# 只要子串更短就覆盖结果,所以即使最短子串有多个,也只会返回第一个
if right-left<le: #
le=right-left
result=[left,right]
left+=1
return [] if le==len(big)+1 else result
4.2.5 找到字符串中所有字母异位词(题438)
给定两个字符串 s 和 p,找到 s 中所有 p 的 异位词 的子串,返回这些子串的起始索引。不考虑答案输出的顺序。
异位词 指由相同字母重排列形成的字符串(包括相同的字符串)。
- 输入: s = “cbaebabacd”, p = “abc”
- 输出: [0,6]
- 解释:
- 起始索引等于 0 的子串是 “cba”, 它是 “abc” 的异位词。
- 起始索引等于 6 的子串是 “bac”, 它是 “abc” 的异位词。
这道题和题567几乎一样,只是需要返回每个子串的起始位置,答案就不写了,同样的题还有《剑指 Offer II 015. 字符串中的所有变位词》。
class Solution(object):
def findAnagrams(self, s, p):
"""
:type s: str
:type p: str
:rtype: List[int]
"""
if len(p)>len(s):
return []
else:
from collections import Counter
count1=dict(Counter(p))
need=len(p) #所需字符的总次数
result=[]
for right in range(len(s)):
ch=s[right]
"""
如果ch是所需的字符,就将ch需要的次数减一,
但是ch次数>0时,才表示这个字符还需要,此时才有need+1
而且要先计算need次数,因为ch次数先操作会导致need统计错误,类似于计算窗口的值再移动窗口
"""
if ch in count1:
if count1[ch]>0:
need-=1
count1[ch]-=1
"""
窗口是固定大小,左指针跟随右指针移动,同时维护需求字典
一开始窗口还不到s1长度,此时left会小于0。left=0是窗口第一次右移
"""
left=right-len(p)
if left>=0:
ch=s[left]
if ch in count1:
if count1[ch]>=0:
need+=1
count1[ch]+=1
if need==0:
result.append(left+1)
return result
4.2.6 串联所有单词的子串(题30)
题目链接
class Solution:
def findSubstring(self, s: str, words: List[str]) -> List[int]:
# word的所有排列组合和元素顺序无关,可以考虑使用字典,不看具体单词只看元素
from collections import Counter
# 将words中每个元素统计其次数存入字典
cnw=dict(Counter(words))
le1=len("".join(words)) # 匹配子串总长度,也等于滑动窗口长度
le2=len(words[0]) # 每个word等长
need=len(words) # need表示总共需要的元素数,不等于cnw长度,因为有键是多个,坑死我了
res=[] # 记录匹配子串的起始位置
for start in range(0,le2): # s的分词方式有多种,都需要遍历到
#print("start:",start)
for right in range(start+le2,len(s)+1,le2):#还是要分割成若干个单词,间隔le2
# 遍历右指针,如果碰到需要的单词,就将其需要次数减1,如果次数大于0,就将总次数减1
# 假如word长为3,即le2=3,右指针就从3开始遍历,每次加入的字符长度都是3
ch=s[right-le2:right]
if ch in cnw:
if cnw[ch]>0:
need-=1
cnw[ch]-=1
#print("r:",ch,cnw,need)
left=right-le1 # 窗口是固定大小,长为le。left=0时刚好是要第一次滑动窗口
if left>=le2:
ch=s[left-le2:left]
if ch in cnw:
if cnw[ch]>=0:
need+=1
cnw[ch]+=1
#print(ch,cnw,need)
if need==0:
res.append(left)
# 每次起点位置遍历完,need 和cnw上一次被改了,需要重置
need=len(words)
cnw=dict(Counter(words))
return res
后续有空再补。
904-水果成篮(opens new window)
159-至多包含两个不同字符的最长子串
340-至多包含 K 个不同字符的最长子串
30-串联所有单词的子串
239- 滑动窗口最大值
632-最小区间
727.-最小窗口子序列