数据结构与算法---分治---最大连续子序列和

分治（Divide And Conquer）

分治，分而治之。先分后治
分治的一般步骤为：

1. 将原问题分解成若干个规模比较小的子问题（子问题和原问题的结构一样，只是规模不一样）
2. 子问题又不断分解成规模更小的子问题，直到不能再分解（直到可以轻易计算出子问题的解）
3. 利用子问题的解推导出原问题的解

因此，分治策略非常适合用递归
需要注意的是：子问题之间是相互独立的

分治的应用：快速排序、归并排序、大数乘法

主定理

分治策略通常遵守一种通用模式：
解决规模为n的问题，分解成a个规模为n/b的子问题，然后在O(n^d)时间内将子问题的解合并起来。
算法运算时间为：T(n) = aT(n/b) + O(n^d)，a>0，b>1，d>=0

比如，归并排序的运行时间是：T(n) = 2T(n/2) + O(n)，套用上面的图表，则T(n) = O(nlogn)

问：为何使用分治策略后，性能会有所提升？

假如要排序n个数据
数据之间需要进行比较，假如两两比较，比如冒泡，需要n^2次
如果分为n/2
左边n/2两两比较，需要n/2*n/2 = n^2/4
右边也是n^2/4
左右加起来是n^2/2

再合起来的时间为O(merge)。如果合并起来的时间小于n^2/2，那么分治策略就是提升性能的。

---

最大连续子序列和

53. 最大子序和

给定一个长度为n的整数序列，求它的最大连续子序列和
比如：-2，1，-3，4，-1，2，1，-5，4的最大连续子序列和为4 - 1 + 2 + 1 = 6

概念区分：
子序列可以不连续；
子串、子数组、子区间必须是连续的；

---

解法一：暴力法

穷举出所有可能的连续子序列，并计算出它们的和，最后取它们中的最大值。

package divide;

public class MaxSubValue {
	public static void main(String[] args)
	{
		int[] array = {-2, 1, -3, 4, -1, 2, 1, -5, 4};
		
		System.out.println(maxSubArray(array));
		
	}
	
	public static int maxSubArray(int[] nums) {
		//边界条件
		if (nums == null || nums.length == 0) return 0;
		
		int max = nums[0];
		for (int begin = 0; begin < nums.length; begin++) {
			for (int end = begin; end < nums.length; end++) {
				int sum = 0;
				for (int i = begin; i <= end; i++) {
					sum += nums[i];
				}
				
				max = Math.max(max, sum);
			}
		}
		return max;
    }
}

时间复杂度：O(n^3)

解法二：暴力法的优化

从代码可以看出，第一种暴力解法并没有利用前面已有的计算结果，而是每次都从begin加到end，其实，可以利用前面的已有结果加end即可。

	public static int maxSubArray1(int[] nums) {
		//边界条件
		if (nums == null || nums.length == 0) return 0;
		
		int max = nums[0];
		for (int begin = 0; begin < nums.length; begin++) {
			int sum = 0;
			for (int end = begin; end < nums.length; end++) {
				sum += nums[end];
				max = Math.max(max, sum);
			}
		}
		return max;
    }

时间复杂度：O(n^2)

---

解法三：分治法

将序列均匀的分割成2个子序列
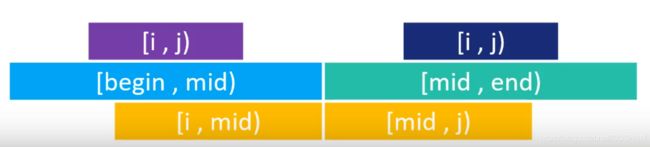
[begin, end) = [begin, mid) + [mid, end), mid = (begin + end) >> 1

假设[begin, end)的最大连续子序列的和是S[i,j)，那么，有三种可能：

• [i, j)存在于[begin, mid)中，同时S[i, j)也是[begin, mid)的最大连续子序列和
• [i, j)存在于[mid, end)中，同时S[i, j)也是[mid, end)的最大连续子序列和
• [i, j)一部分存在于[begin, mid中，另一部分存在于[mid, end)中
  [i, j) = [i, mid) + [mid, j)
  S[i, mid) = max{S[k, mid)}，begin <= k < mid
  S[mid, j) = max{S[mid, j)}，mid < k <= end

	public static int maxSubArray2(int[] nums) {
		//边界条件
		if (nums == null || nums.length == 0) return 0;
		return maxSubArray(nums, 0, nums.length);
    }
	
	public static int maxSubArray(int[] nums, int begin, int end)
	{
		//递归的边界条件
		if (end - begin < 2) return nums[begin];
		int mid = (begin + end) >> 1;
		
		//全左最大值
		int allLeftMax = maxSubArray(nums, begin, mid);
		
		//全右最小值
		int allRightMax = maxSubArray(nums, mid, end);
		
		//一部分在左，一部分在右
		int partLeftAndPartRightMax = 0;
		
		int partRightMax = 0;
		int partRightSum = 0;
		for (int i = mid; i < end; i++) {
			partRightSum += nums[i];
			partRightMax = Math.max(partRightSum, partRightMax);
		}
		
		int partLeftMax = 0;
		int partLeftSum = 0;
		for (int i = mid - 1; i >= begin; i--) {
			partLeftSum += nums[i];
			partLeftMax = Math.max(partLeftSum, partLeftMax);
		}
		
		partLeftAndPartRightMax = partLeftMax + partRightMax;
		
		return Math.max(partLeftAndPartRightMax, Math.max(allLeftMax, allRightMax));
	}
	

时间复杂度分析：
T(n) = T(n/2) + T(n/2) + O(n)
可以得知，时间复杂度为O(nlogn)