树与二叉树
树
树的基本概念
- 节点:节点包括一个数据元素及若干指向其他子树的分支。
- 节点的度:节点所拥有子结点的个数称为节点的度。
- 叶子结点:度为0的节点成为叶结点,叶结点也称为终端节点。
- 分支节点:度不为0的节点称为分支节点,分支节点又称非终端节点。一棵树中排除叶结点外的所有节点都是分支节点。
- 内部节点:只拥有父节点,和子节点的节点
- 祖先节点:从根节点到该节点所经分支上的所有节点。
- 子孙节点:以某节点为根节点的子树中所有节点
- 双亲节点:树中某节点有孩子节点,则这个节点称为它孩子节点的双亲节点,双亲节点也成为前驱节点。
- 孩子节点:树中一个节点的子树的根节点称为该节点的孩子节点,孩子节点也称为后继节点。
- 兄弟节点:具有相同双亲节点的节点称为兄弟节点。
- 树的度:树中所有节点的度的最大值成为该树的度。
- 节点的层次:从根节点到树中某节点所经路径上的分支也称为该节点的层次,根节点的层次为1,其他节点层次是双亲节点层次加1
二叉树的重要特性
-
在二叉树的第i层上最多有 2 i − 1 2^{i-1} 2i−1个结点( i ≥ 1 i\geq1 i≥1);
-
在深度为K的二叉树上最多有 2 k − 1 2^{k}-1 2k−1个结点( k ≥ 1 k\geq1 k≥1);
-
对于任何一棵二叉树,如果其叶子结点数为 n 0 n_{0} n0,度为2的结点数为 n 2 n_{2} n2,则 n 0 = n 2 + 1 n_{0}=n_{2}+1 n0=n2+1
-
如果对一棵有n个结点的完全二叉树的结点按层序编号(从第一层到最后一层,每层从左到右),则对任意结点 i ( 1 ≤ i ≤ n ) i(1 \leq i\leq n) i(1≤i≤n)有如下规则:

二叉树的先序、中序、后序遍历序列
二叉树的遍历主要有三种:(注意根在顺序里面的位置)
(1)先(根)序遍历(根左右)
(2)中(根)序遍历(左根右)
(3)后(根)序遍历(左右根)
举个栗子:
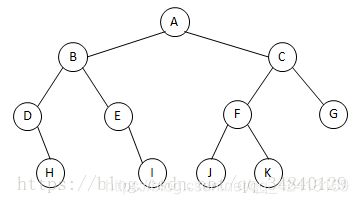
先(根)序遍历(根左右):A B D H E I C F J K G
中(根)序遍历(左根右) : D H B E I A J F K C G
后(根)序遍历(左右根) : H D I E B J K F G C A
以后(根)序遍历为例,每次都是先遍历树的左子树,然后再遍历树的右子树,最后再遍历根节点,以此类推,直至遍历完整个树。
二叉树的反向构造
已知:
- 前序:ABHFDECG
- 中序:HBEDFAGC
通过前序规则我们可以知道:根节点为A
通过中序规则和根节点A我们可以推导出如下图:
我们通过中序规则将左子树的根节点推算出来为B,我们再根据前序规则推算出下图:

再通过中序规则推算出:
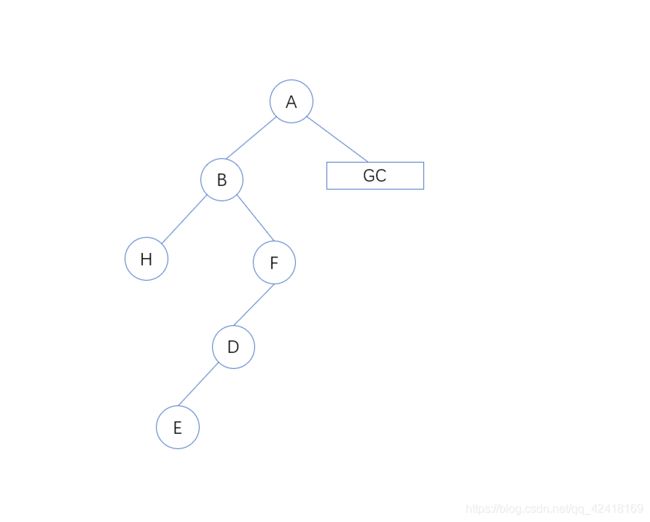
最后再根据前序规则推算出右子树的根节点为C:
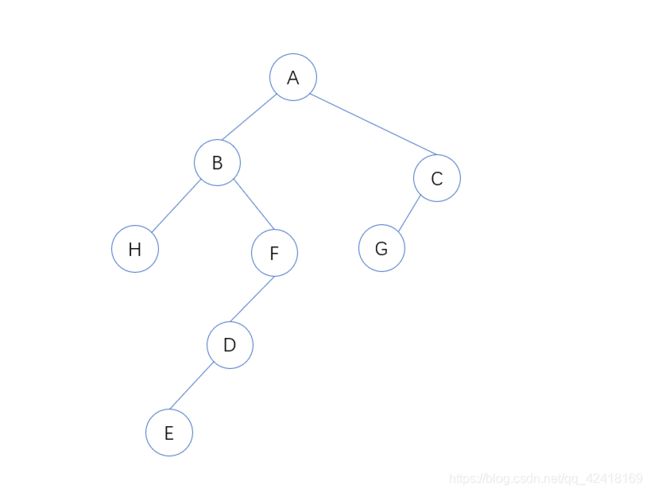
树转二叉树
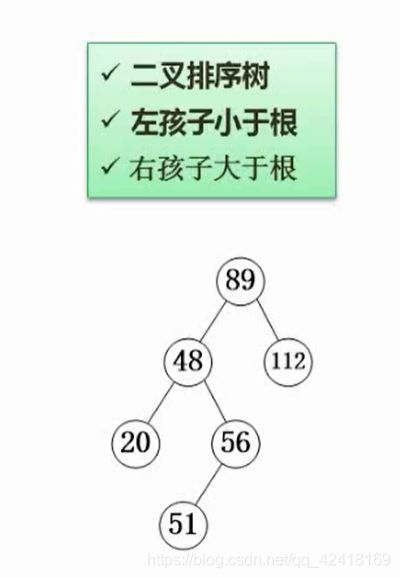
查找二叉树(排序二叉树)
插入结点
- (在树里面必须是唯一的)若该键值结点已存在,则不再插入,如:48;
- 若查找二叉树为空树,则以新结点为查找二叉树;
- 将要插入结点键值与插入后父结点键值比较,就能确定新结点是父结点的左子结点,还是右子结点。
删除结点
- 若待删除结点是叶子结点,则直接删除;
- 若待删除结点只有一个子结点,则将这个子结点与待删除结点的父结点直接连接,如:56;
- 若待删除的结点有两个子结点,则在其左子树上,用中序遍历寻找关键值最大的结点s,用结点s的值代替结点p的值,然后删除节点s,例如89
最优二叉树(哈夫曼树)
推荐文章:https://blog.csdn.net/qq_29519041/article/details/81428934
什么是哈夫曼编码
常用在压缩数据领域的一种编码,是一种无损编码,将文件内容无损压缩以减少传输带宽的消耗,解压后的文件与源文件是一样的
基本概念
- 树的路径长度:就是结点到结点之间的路径,一个结点到另一个结点为1
- 权:结点代表的字符串出现的频率,频率越高,权越高
- 带权路径长度:叶子结点到根节点的路径长度×叶子结点本身的权所得到的数值
- 树的带权路劲长度:就是这棵树上所有的叶子结点的带权路劲长度的总和
- 注意:哈夫曼树所有的叶子节点必须是最原始的权,不能是衍生的权
哈弗曼树的构造方法
首先统计出每种字符出现的频率!(也可以是概率)//权值
--------------------------------------------------
例如:频率表 A:60, B:45, C:13 D:69 E:14 F:5 G:3
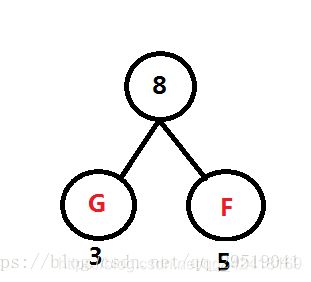
第一步:找出字符中最小的两个,小的在左边,大的在右边,组成二叉树。在频率表中删除此次找到的两个数,并加入此次最小两个数的频率和。
F和G最小,因此如图,从字符串频率计数中删除F与G,并返回G与F的和 8给频率表
频率表 A:60, B:45, C:13 D:69 E:14 FG:8
最小的是 FG:8与C:13,因此如图,并返回FGC的和:21给频率表。
如图
---------------------------------------------------------------------------------------------------
重复第一步:
------------------------------------------------ ---------------------------------------------------
频率表 A:60 B: 45 D: 69 E: 14 FGC: 21
如图
-----------------------------------------------------------------------------------------------------
重复第一步
-----------------------------------------------------------------------------------------------------
频率表 A:60 B: 45 D: 69 FGCE: 35
-----------------------------------------------------------------------------------------------------
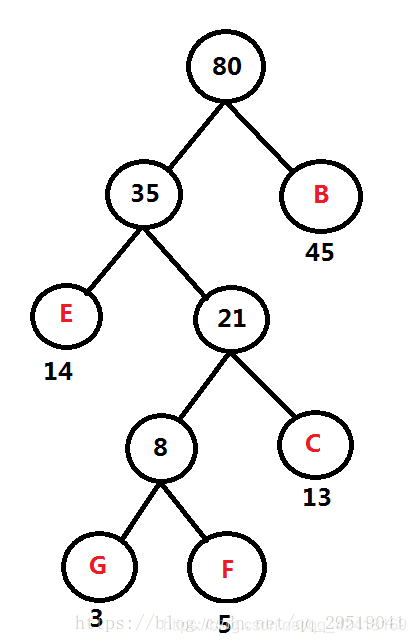
重复第一步
-----------------------------------------------------------------------------------------------------
频率表 A:60 D: 69 FGCEB: 80
- 注意:哈夫曼树所有的叶子节点必须是最原始的权,不能是衍生的权,所以最后两个数不用比较,直接成为一个新树
-----------------------------------------------------------------------------------------------------
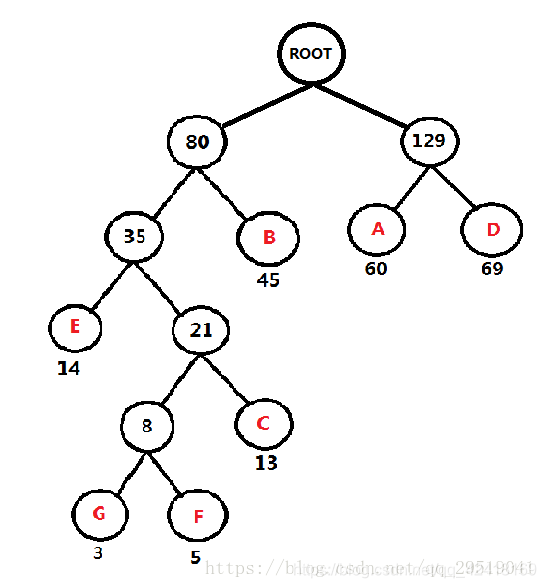
重复第一步
-----------------------------------------------------------------------------------------------------
频率表 AD:129 FGCEB: 80
线索二叉树
概念
对于n个结点的二叉树,在二叉链存储结构中有n+1个空链域,利用这些空链域存放在某种遍历次序下该结点的前驱结点和后继结点的指针,这些指针称为线索,加上线索的二叉树称为线索二叉树。
本质
二叉树的遍历本质上是将一个复杂的非线性结构转换为线性结构,使每个结点都有了唯一前驱和后继(第一个结点无前驱,最后一个结点无后继)。对于二叉树的一个结点,查找其左右子女是方便的,其前驱后继只有在遍历中得到。为了容易找到前驱和后继,有两种方法。一是在结点结构中增加向前和向后的指针,这种方法增加了存储开销,不可取;二是利用二叉树的空链指针。
优缺点
优点:
- 利用线索二叉树进行中序遍历时,不必采用堆栈处理,速度较一般二叉树的遍历速度快,且节约存储空间。
- 任意一个结点都能直接找到它的前驱和后继结点
缺点:
- 结点的插入和删除麻烦,且速度也较慢。
- 线索子树不能共用
将二叉树转化为线索二叉树
转换为:前序线索二叉树
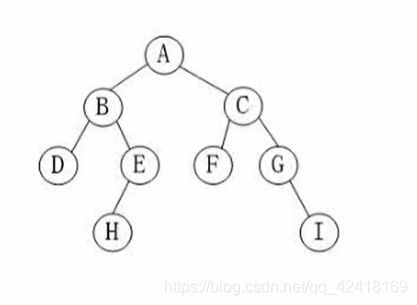
很简单,我们只需要将二叉树以前序遍历的方式写出来我们就知道了
前序遍历:A,B,D,E,H,C,F,G,I
看顺序我们就知道:
D的前序为B,后序为E
H的前序为E,后序为C
F的前序为C,后序为G
I的前序为G,后序为null
转换为:中序线索二叉树
中序遍历:D,B,H,E,A,F,C,G,I

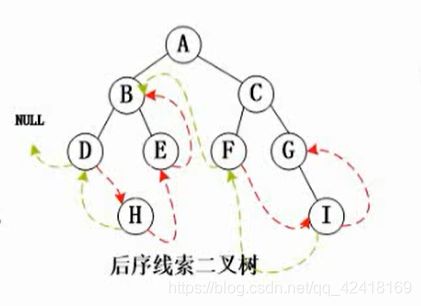
转换为:后序线索二叉树
后序遍历:D,H,E,B,F,I,G,C,A