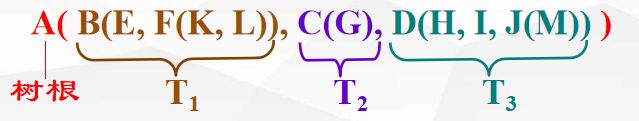大二数据结构5（树与二叉树）

一. 树

【1】树的定义

数据对象D：是具有相同特性的数据元素的集合
数据关系R：
若D为空集，则为空树
否则：
（1）在D中存在唯一的根
（2）n>1时，其余均为根的子树

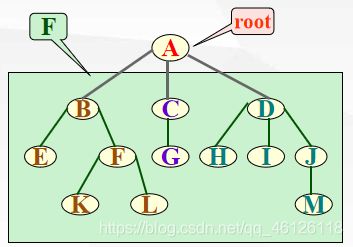
【2】树的表示

【3】树与线性结构对比

【4】一些基本术语

结点:数据元素+若干指向子树的分支
结点的度:分支的个数
树的度:树中所有结点的度的最大值
叶子结点:度为零的结点
分支结点:度大于零的结点
从根到结点的路径：由从根到该结点所经分支和结点构成
孩子(子)结点、双亲(父)结点
兄弟结点、堂兄弟
祖先结点、子孙结点
结点的层次:假设根结点的层次为1，其他结点层次等于其双亲结点的层次加1
树的深度：树中叶子结点所在的最大层次
有序树：子树之间存在确定的次序关系。
无序树：子树之间不存在确定的次序关系。
森林：是m（m≥0）棵互不相交的树的集合
任何一棵非空树是一个二元组 Tree = （root，F）
其中：root 被称为根结点 F 被称为子树森林

二.二叉树

1.定义

二叉树或为空树，或是由一个根结点加上两棵分别称为左子树和右子树的、互不相交二叉树组成。

2. 二叉树的五种基本形态

3.二叉树的重要特性

性质：

1. 二叉树第 i 层上至多有2^i-1结点。(i≥1)
2. 深度为 k 的二叉树上至多含2^k-1 个结（k≥1）
3. 对任何一棵二叉树，若它含有 n₀ 个叶子结点、n₂ 个度为 2 的结点，
   则：n₀= n₂+1。

4. 两类特殊的二叉树

【1】满二叉树：指的是深度为k且含有2^k-1个结点的二叉树。

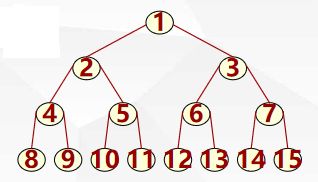
【2】完全二叉树：树中所含的 n 个结点和满二叉树中编号为 1 至 n 的结点一一对应。

由完全二叉树的定义有以下结论：
（1）叶子结点只可能在层次最大的两层上出现（最下两层）；
（2）满二叉树一定是完全二叉树，反之不然；
（3）完全二叉树中，若某结点无左孩子，则该结点一定无右孩子；
（4）对任一结点，若其右分支下的子孙的最大层次为k，则其左分支下的子孙的最大层次必为k或k+1。
性质：

1. 具有 n 个结点的完全二叉树的深度为 |log2n| +1 。

2. 若对含 n 个结点的完全二叉树从上到下，从左至右进行 1 至 n 的编号，则对完全二叉树中任意一个编号为 i 的结点：(1) 若 i=1，则该结点是二叉树的根，无双亲，
   否则，编号为 i/2 的结点为其双亲结点；
   (2) 若 2i>n，则该结点无左孩子， 否则，编号为 2i 的结点为其左孩子结点；
   (3) 若 2i+1>n，则该结点无右孩子结点， 否则，编号为2i+1 的结点为其右孩子结点。

问： 设高度为h的二叉树T无度为1的结点，则二叉树T至少有多少个结点？至多有多少个结点？若二叉树T的叶子总数为，则二叉树T的结点总数为多少？
分析：
（1）由于二叉树T无1度结点，从而当从第二层至第h层每层只有两个结点时，T的总结点数最少，而第一层只有树根，从而，T至少有：2(h-1)+1=2h-1个结点；
（2）由二叉树的性质2知，T至多有2^h-1个结点；
（3）设n₀、n₁、n₂、n分别为T的叶子结点数、1度结点数、2度结点数、结点总数，则有：n₀=m，n₁=0
由二叉树的性质3有：n₀=n₂ +1，有n₂= n₀-1
从而，n=n₀+n₁+n₂=n₀+0+n₀-1=2n₀-1=2m -1

5. 二叉树的存储结构

1）.二叉树的顺序存储表示

#define MAX_TREE_SIZE 100
typedef TElemType SqBitree[MAX_TREE_SIZE];
SqBitree bt;

2） 二叉树的链式存储表示

A 二叉链表

‘1. 结构特点：

typedef struct BiTNode{

   TElemtype data;
   struct BiTNode *lchild,*rchild;
   
}BiTNode,*BiTree;

B.三叉树

1. 结点结构:
   

typedef struct BiTNode{

   TElemtype data;
   struct BiTNode *parent *lchild,*rchild;
   
}BiTNode,*BiTree;

6.二叉树的遍历

A 什么是遍历？

 顺着某一条搜索路径巡访二叉树中的结点，使得每个结点均被访问一次，而且仅被访问一次。
 “访问”的含义可以很广，如：输出结点的信息等。
 “遍历”是任何类型均有的操作，对线性结构而言，只有一条搜索路径(因为每个结点均只有一个后继)，故不需要另加讨论。而二叉树是非线性结构，每个结点有两个后继，则存在如何遍历即按什么样的搜索路径遍历的问题。

B.遍历路径

对“二叉树”而言，可以有三条搜索路径：

1. 先上后下的按层次遍历；
2. 先左（子树）后右（子树）的遍历；
3. 先右（子树）后左（子树）的遍历。

C 遍历算法

【1】先\后（根）序的遍历算法：
A. 递归

void preorder(BiTNode *t)//前序
{
    if(t!=NULL)
    {    count<<t->data;
        preorder(t->rchild);
        preorder(t->rchild);
    }
}
void postorder(BiTNode *t)//后序
{
    if(t!=NULL)
    {     preorder(t->rchild);
        preorder(t->rchild);
       count<<t->data;
    }
}
void postorder(BiTNode *t)//中序
{
    if(t!=NULL)
    {     preorder(t->rchild);
       count<<t->data;  
      preorder(t->rchild);
    }
}

时间效率:O(n) //每个结点只访问一次
空间效率:O(n) //栈占用的最大辅助空间

B.非递归描述
【1】利用栈的前序和中序
A前序

void preorder1(BiTree root)
{
    BiTree s[MAX_TREE_SIZE],p;
    int top;
    top=0;
    p=root;
    while(p||top>0)
    {
        while(p)
        {
            cout<<p->data<<" ";
            top++;
            s.[top]=p;
            p=p->lchild;   
        }
        if(top>0)
        {
            p=s[top];
            top--;
            p=p->rchild;
        }
    }
    
}

B 后序

void pasorder1(BiTNode t)
{   struct {
    BiTNode *pp;
    int tag;
    
  }ss[MAX_TREE_SIZE];
  int top;
  BiTNode *P;
  top=0;p=t;
  while(p||top>0)
  {
      while(p)
      {
          top++;
          ss[top].tag=0;
          ss[top].pp=p;
          p=p->lchild;
          
      }
      if(top>0)
         if(ss[top].tag==0)
      {
          ss[top].tag=1;
          p=ss[top].pp;
          p=p->rchild;
      }
        else 
      {
          p=ss[top].pp;
          cout<<p->data<<"  ";
          top--;
          p=NULL;
      }
  }
   
}

C 层次遍历

void leveltree(BiTree *t)
{
      BiTree s[100],p;
      int front rear;
    front=rear=0;
    p=t;
     if(t!=NULL)
     {
         rear++;
         s[rear]=p;
         while(front!=rear)
         {  front++;
            p=s[front];
            count<<p->data;
            if(p->lchild)
            {
                rear++;
                s[rear]=p->lchild;
                
            }
             if(p->rchild)
            {
                rear++;
                s[rear]=p->rchild;
                
            }
             
         }
     }
}

7. 遍历算法的应用举例

1） 统计二叉树中叶子结点的个数

int addTnode(Bitree *t)
{
    if(t=NULL) return 0;
    else 
        if(t->rchild==NULL&&t->lchild==NULL)
          n++;
    addTnode(t->rchild);
    addTnode(t->lchild);
    return n;
} 

2） 求二叉树的深度
算法基本思想: 二叉树的深度应为其左、右子树深度的最大值加1。由此，需先分别求得左、右子树的深度，算法中“访问结点”的操作为：求得左、右子树深度的最大值，然后加1。

int findtree(BiTree *t)
{    int l,r;
    if(t==NULL) return 0;
    else 
    {
        l=findtree(t->lchhild);
        r=findtree(t->rchild);
        if(l<r)  return r+1;
        else return l+1;
    }
}

3） 复制二叉树

void copytree(BiTree t1,BiTree t2)
{    if(t1==NULL)
       t2=NULL;
     else {
       t2=new BiTNode;
       t2->data=t1->data;
       t2->lchild=NULL;
       t2->rchild=NULL;
       copytree(t1->rchild,t2->rchild);
       copytree(t1->lchild,t2->lchild);
     }
    
}

4）. 建立一个二叉树

void creatree(BiTree &t);
{
    char ch;
    count<<ch<<" ";
    t->data=ch;
    if(ch!='@')
    {
        t=new BiTNode;
        creatree(t->lchild);
        creatree(t->rchild);
        
    }
    else 
        t=NULL;
}

三.二叉树总汇

#include 
#include 
using namespace std;
//；二叉树的顺序储存结构
#define MAX_TREE 10000;
typedef  Telemtype SiTree[MAX_PATH];
SiTree bT;
//二叉树的链式储存结构
typedef struct SiTNode{
      Telemtype data;
      struct SiTNode *lchild,*rchild;
}SiTNode,*SiTree;
//三叉树的链式结构
typedef struct SiTNode{
  Telemtype data;
    struct SiTNode *parent,*lchild,*rchild;

}SiTNode,*SiTree;
//遍历
//前中后序递归遍历
void preTree(SiTNode *t)
{
    if(t=NULL)
       exit(0);
    else 
    {
       cout<<t->data;
        preTree(t->lchild);
        preTree(t->rchild); 
    }
        
}
void minTree(SiTNode *t)
{
    if(t=NULL)
       exit(0);
    else 
    {
        preTree(t->lchild);
       cout<<t->data;
        preTree(t->rchild); 
    }
        
}
void lastTree(SiTNode *t)
{
    if(t=NULL)
       exit(0);
    else 
    {
        preTree(t->lchild);
        preTree(t->rchild);
        cout<<t->data;
    }
        
}

//非递归算法遍历
//前中序遍历
void preTree(SiTNode *t)
{ 
    SiTree s[MAX_PATH],p;
    int top=0;
    while(p||top>0)
    {
        while(p)
        {
            top++;
            s[top]=p;
          cout<<p->data;
            p=p->lchild;
        }
        if(top>0)
        {
         
            p=s[top];
            top--;
            p=p->rchild;
        }
    }


}
//后序非递归遍历
void  lastTree(SiTree *t)
{
    struct {
        BiTNode *pp;
        int tag;
    }ss[MAX_PATH];
    int top;
    top=0;
    SiTNode *P;
    p=t;
    while(p||top>0)
    {
        while(p)
        {
            top++;
            ss[top].pp=p;
            ss[top].tag=0;
            p=p->lchild;
            
        }
        if(top>0)
        {
            if(ss[top].tag==0)
            {
                ss[top].tag=1;
                p=ss[top].pp;
                p=p->rchild;
            }
            else{
                p=ss[top].pp
                cout<<p->data;
                top--;
                p=NULL;
            }
        }
    }
}
//层次遍历
void laveltree(SiTNode &t)
{   BiTree s[MAX_PATH],p;
int front rear;
p=t;
    if(t!=NULL)
    {
        rear++;
        s[top]=p;
        while(front!=rear)
        {
            front++;
            p=s[front];
            cout<<p->data;
            if(p->lchild)
            {
                rear++;
                s[rear]=p->lchild;
                
            }
            if(p->rchild)
            {
                rear++;
                s[rear]=p->rchild;
                
            }
        }
    }
}