数据结构实验二 二叉树的操作与实现

系列文章：
数据结构实验一 线性表、堆栈和队列的操作与实现
数据结构实验二 二叉树的操作与实现
数据结构实验三 图的操作与实现
数据结构实验四 查找和排序算法实现

一、实验目的：

1、领会二叉链存储结构和掌握二叉树中的各种基本运算算法设计；
2、领会线索二叉树的构造过程以及构造二叉树的算法设计；
3、领会哈夫曼树的构造过程以及哈夫曼编码的生成过程；
4、掌握二叉树遍历算法的应用，熟练使用先序、中序、后序3种递归遍历算法进行二叉树问题的求解；

二、使用仪器、器材

微机一台
操作系统：WinXP
编程软件：C/C++编程软件

三、实验内容及原理

填入自己的内容（思路或算法流程图、源代码、说明等）

1、教材P247实验题1：实现二叉树的各种基本运算的算法

编写一个程序btree.cpp，实现二叉树的基本运算，并在此基础上设计一个程序exp7-1.cpp完成以下功能。
（1）由图7.33所示的二叉树创建对应的二叉链存储结构b，该二叉树的括号表示串为“A(B(D,E(H(J,K(L,M(,N))))),C(F,G(,i)))”。
（2）输出二叉树b。
（3）输出‘H’结点的左、右孩子结点值。
（4）输出二叉树b的高度。
（5）释放二叉树b。

#include 
using namespace std;

struct TreeNode{
    char val;
    TreeNode* left;
    TreeNode* right;
    TreeNode(char v){
        this->val = v;
        this->left = NULL;
        this->right = NULL;
    }
    TreeNode(char v,TreeNode* l,TreeNode *r){
        this->val = v;
        this->left = l;
        this->right = r;
    }
};

/*
通过字符串递归创建二叉树，格式为
A(B(D,E(H(J,K(L,M(,N))))),C(F,G(,i)))
*/
TreeNode* init(string p){
    if(p == ""){
        return NULL;
    }
    TreeNode* t = new TreeNode(p[0]); //p的第一个字符就是根节点的值
    if(p.length() == 1){
        return t; //没有左右子树的时候
    }
    int lf = 0; //经历了多少个左括号
    int i = 2; 
    //----------------------------
    //从A(B(D,E(H(J,K(L,M(,N))))),C(F,G(,i)))
    //分离出B(D,E(H(J,K(L,M(,N))))) 和 C(F,G(,i))
    while(i < p.length() - 1 && ((lf == 0 && p[i] != ',') || lf != 0)){
        if(p[i] == '('){
            ++lf;
        }
        if(p[i] == ')'){
            --lf;
        }
        ++i;
    }
    t->left = init(p.substr(2,i-2));
    if(i != p.length() - 1){
        t->right = init(p.substr(i+1,p.length() - 2 - i));
    }
    return t;
}

/*
前序遍历
*/
void preorderTraversal(TreeNode* node){
    if(node == NULL){
        //如果节点为空，直接返回即可
        return;
    }
    cout << node->val << " ";
    preorderTraversal(node->left);
    preorderTraversal(node->right);
}

/*
中序遍历
*/
void inorderTraversal(TreeNode* node){
    if(node == NULL){
        //如果节点为空，直接返回即可
        return;
    }
    inorderTraversal(node->left);
    cout << node->val << " ";
    inorderTraversal(node->right);
}

/*
后序遍历
*/
void postorderTraversal(TreeNode* node){
    if(node == NULL){
        //如果节点为空，直接返回即可
        return;
    }
    postorderTraversal(node->left);
    postorderTraversal(node->right);
    cout << node->val << " ";
}



/*
寻找指定值的节点（使用递归查找）
*/
TreeNode* find(TreeNode* node,char c){
    if(node == NULL || node->val == c){
        return node; //为空或者找到了，直接返回当前节点即可
    }
    TreeNode* f = find(node->left,c);  //寻找他的左子树
    if(f){
        //如果在左子树找到了，直接返回
        return f;
    }
    //左子树找不到则寻找右子树
    f = find(node->right,c);
    return f;  //如果找到，直接返回，就算没找到也是返回NULL
}

/*
利用BFS算法求二叉树的高度
*/
int getHeight(TreeNode* tree){
    if(tree == NULL){
        return 0;
    }
    queue<TreeNode*> q; //队列
    int size = 1; //队列里面不为NULL的元素个数（为了区分层数，会用NULL来做个标记）
    int h = 1;
    q.push(tree); //加入根节点
    q.push(NULL); //加入NULL，作为标记
    TreeNode* t;
    while(size > 0){
        t = q.front(); //取队列的首元素
        q.pop();   //首元素出队
        if(!t){
            //取出的是NULL，说明是个标记
            ++h; //高度+1
            q.push(NULL);   //再加入一个NULL作为下一行的标记
            continue;
        }
        //取出的不是NULL
        --size;  //size-1
        if(t->left){
            //如果他的左孩子存在，则加入队列
            q.push(t->left);
            ++size;
        }
        if(t->right){
            //如果他的右孩子存在，则加入队列
            q.push(t->right);
            ++size;
        }
    }
    return h;
}

/*
递归销毁二叉树
*/
void destory(TreeNode* node){
    if(node == NULL){
        return;  //已经为NULL，无需销毁
    }
    destory(node->left);
    destory(node->right);
    node->left = NULL; //销毁之后需要把指针置空
    node->right = NULL;
    delete node;
}

int main() {
	ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
	// （1）由图7.33所示的二叉树创建对应的二叉链存储结构b，该二叉树的括号表示串为“A(B(D,E(H(J,K(L,M(,N))))),C(F,G(,i)))”。
    TreeNode* b = init("A(B(D,E(H(J,K(L,M(,N))))),C(F,G(,I)))");
    // （2）输出二叉树b。
    cout << "preorder traversal:" << endl;
    preorderTraversal(b);
    cout << endl;
    cout << "inorder traversal:" << endl;
    inorderTraversal(b);
    cout << endl;
    cout << "postorder traversal:" << endl;
    postorderTraversal(b);
    cout << endl;
    
    // （3）输出‘H’结点的左、右孩子结点值。
    TreeNode* h = find(b,'H');
    if(h){
        if(h->left){
            cout << "H's left child is " << h->left->val << endl;
        }else{
            cout << "H's left child is NULL" << endl;
        }
        if(h->right){
            cout << "H's right child is " << h->right->val << endl;
        }else{
            cout << "H's right child is NULL" << endl;
        }
        
    }else{
        cout << "H Not Found!" << endl;
    }
    // （4）输出二叉树b的高度。
    cout << "The height of tree b is " << getHeight(b) << endl;
    // （5）释放二叉树b。
    destory(b);
    b = NULL;
    cout << "destory success!" << endl;
	return 0;
}

2、教材P248实验题3：由遍历序列构造二叉树

编写一个程序exp7-3.cpp，实现由先序序列和中序序列以及由中序序列和后序序列构造一棵二叉树的功能（二叉树种的每个结点值为单个字符），要求以括号表示和凹入表示法输出该二叉树，并用先序遍历序列“ABDEHJKLMNCFGI”和中序遍历序列“DBJHLKMNEAFCGI”以及由中序遍历序列“DBJHLKMNEAFCGI”和后序遍历序列“DJLNMKHEBFIGCA”进行验证。

#include 
using namespace std;

struct TreeNode{
    char val;
    TreeNode* left;
    TreeNode* right;
    TreeNode(char v){
        this->val = v;
        this->left = NULL;
        this->right = NULL;
    }
    TreeNode(char v,TreeNode* l,TreeNode *r){
        this->val = v;
        this->left = l;
        this->right = r;
    }
};

/*
前序遍历
*/
void preorderTraversal(TreeNode* node){
    if(node == NULL){
        //如果节点为空，直接返回即可
        return;
    }
    cout << node->val << " ";
    preorderTraversal(node->left);
    preorderTraversal(node->right);
}

/*
中序遍历
*/
void inorderTraversal(TreeNode* node){
    if(node == NULL){
        //如果节点为空，直接返回即可
        return;
    }
    inorderTraversal(node->left);
    cout << node->val << " ";
    inorderTraversal(node->right);
}

/*
后序遍历
*/
void postorderTraversal(TreeNode* node){
    if(node == NULL){
        //如果节点为空，直接返回即可
        return;
    }
    postorderTraversal(node->left);
    postorderTraversal(node->right);
    cout << node->val << " ";
}

/*
由先序序列和中序序列构造二叉树
*/
TreeNode* initTreeByPreorderTraversalAndInorderTraversal(string preorder,string inorder){
    if(preorder.length() == 0){
        return NULL;
    }
    TreeNode* t = new TreeNode(preorder[0]);
    if(preorder.length() == 1){
        return t;
    }
    //把inorder分成左、右两部分
    int mid = inorder.find(preorder[0]);
    string inorder_left = inorder.substr(0,mid);
    string inorder_right = inorder.substr(mid+1);
    //preorder的格式为 自身节点 左子树 右子树
    //现在需要把他分为左子树和右子树两部分
    // mid = 1;
    // while(mid < preorder.length()){
    //     bool tag = 0;  //因为没法一次结束2层循环，所以需要加上tag标记
    //     //一趟一趟地寻找，指导寻找到某一点在inorder的右子树出现
    //     for(int i = 0;i
    //         if(inorder_right[i] == preorder[mid]){
    //             tag = 1;
    //             break;
    //         }
    //     }
    //     if(tag){
    //         break;
    //     }
    //     ++mid;
    // }
    // string preorder_left = preorder.substr(1,mid-1);
    // string preorder_right = preorder.substr(mid,preorder.length() - mid);
    string preorder_left = preorder.substr(1,inorder_left.length());
    string preorder_right = preorder.substr(1 + inorder_left.length());
    t ->left = initTreeByPreorderTraversalAndInorderTraversal(preorder_left,inorder_left);
    t ->right = initTreeByPreorderTraversalAndInorderTraversal(preorder_right,inorder_right);
    return t;
}

/*
由后序序列和中序序列构造二叉树
*/
TreeNode* initTreeByPostorderTraversalAndInorderTraversal(string postorder,string inorder){
    if(postorder.length() == 0){
        return NULL;
    }
    TreeNode* t = new TreeNode(postorder[postorder.length() - 1]); //后续遍历的最后一个值是自身节点的值
    if(postorder.length() == 1){
        return t;
    }
    //把inorder分成左、右两部分
    int mid = inorder.find(postorder[postorder.length() - 1]);
    string inorder_left = inorder.substr(0,mid);
    string inorder_right = inorder.substr(mid+1);
    string postorder_left = postorder.substr(0,inorder_left.length());
    string postorder_right = postorder.substr(inorder_left.length(),inorder_right.length());
    t->left = initTreeByPostorderTraversalAndInorderTraversal(postorder_left,inorder_left);
    t->right = initTreeByPostorderTraversalAndInorderTraversal(postorder_right,inorder_right);
    return t;
}

/*
括号表示法
*/
string printTreeByParenthesizedNotation(TreeNode* t){
    if(!t){
        return "";
    }
    string s = string(1,t->val);
    if(!t->left && !t ->right){
        return s;
    }
    s.append("(");
    s.append(printTreeByParenthesizedNotation(t->left));
    if(t->right){
        s.append(",");
        s.append(printTreeByParenthesizedNotation(t->right));
    }
    s.append(")");
    return s;
}

/*
凹入表示法
*/
void printTreeByConcaveNotation(TreeNode* t,int i = 0){
    if(t){
        cout << string(i * 3,' ') << t->val << endl;
        printTreeByConcaveNotation(t->left,i+1);
        printTreeByConcaveNotation(t->right,i+1);
    }
}

/*
递归销毁二叉树
*/
void destory(TreeNode* node){
    if(node == NULL){
        return;  //已经为NULL，无需销毁
    }
    destory(node->left);
    destory(node->right);
    node->left = NULL; //销毁之后需要把指针置空
    node->right = NULL;
    delete node;
}

int main() {
	ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
    // cout << "用先序遍历序列“ABDEHJKLMNCFGI”和中序遍历序列“DBJHLKMNEAFCGI”验证" << endl;
    TreeNode* t1 = initTreeByPreorderTraversalAndInorderTraversal("ABDEHJKLMNCFGI","DBJHLKMNEAFCGI");
    //括号表示法：
    string s = printTreeByParenthesizedNotation(t1);
    cout << s << endl;
    //凹入表示法
    printTreeByConcaveNotation(t1);
    //由中序遍历序列“DBJHLKMNEAFCGI”和后序遍历序列“DJLNMKHEBFIGCA”进行验证
    TreeNode* t2 = initTreeByPostorderTraversalAndInorderTraversal("DJLNMKHEBFIGCA","DBJHLKMNEAFCGI");
    //括号表示法：
    cout << printTreeByParenthesizedNotation(t2) << endl;
    //凹入表示法
    printTreeByConcaveNotation(t2);
    //程序运行结束之后需要销毁二叉树
    destory(t1);
    destory(t2);
    t1 = NULL;
    t2 = NULL;
	return 0;
}

3、教材P248实验题5：构造哈夫曼树生成哈夫曼编码

编写一个程序exp7-5.cpp，构造一棵哈夫曼树，输出对应的哈夫曼编码和平均查找长度，并对下表（表7.8）所示的数据进行验证。

#include 
using namespace std;

struct TreeNode{
    char word[5];   //单词
    int weight;     //权值
    TreeNode* left;
    TreeNode* right;
    TreeNode(const char* lst,int w){
        strcpy(word,lst);
        this->weight = w;
        this->left = NULL;
        this->right = NULL;
    }
    TreeNode(const char* lst,int w,TreeNode* l,TreeNode *r){
        strcpy(word,lst);
        this->weight = w;
        this->left = l;
        this->right = r;
    }
};

/*
计算带权路径长度
*/
int calcularLength(TreeNode* t,int depth = 0){
    if(!t){
        return 0;  
    }
    if(!t->left && !t->right){
        // cout << t->weight * depth << endl;
        return t->weight * depth;   //一个节点的路径长度=权值*深度
    }
    return calcularLength(t->left,depth + 1) + calcularLength(t->right,depth+1);
}

/*
输出每个单词的哈夫曼编码
*/
char s[128];
void printHuffmanCoding(TreeNode* t,int i = 0){
    if(t){
        if(!t->left && !t->right){
            s[i] = 0;  //需要把这个位置置为0，当做结束标记
            printf("%s:%s\n",t->word,s);
        }
        if(t->left){
            s[i] = '0';  //哈夫曼编码，左边是0，右边是1
            printHuffmanCoding(t->left,i+1);
        }
        if(t->right){
            s[i] = '1';
            printHuffmanCoding(t->right,i+1);
        }
    }
}

/*
递归销毁二叉树
*/
void destory(TreeNode* node){
    if(node == NULL){
        return;  //已经为NULL，无需销毁
    }
    destory(node->left);
    destory(node->right);
    node->left = NULL; //销毁之后需要把指针置空
    node->right = NULL;
    delete node;
}

int main() {
	ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
    list<TreeNode*> lst;
    lst.push_back(new TreeNode("The",1192));
    lst.push_back(new TreeNode("of",677));
    lst.push_back(new TreeNode("a",541));
    lst.push_back(new TreeNode("to",518));
    lst.push_back(new TreeNode("and",462));
    lst.push_back(new TreeNode("in",450));
    lst.push_back(new TreeNode("that",242));
    lst.push_back(new TreeNode("he",195));
    lst.push_back(new TreeNode("is",190));
    lst.push_back(new TreeNode("at",181));
    lst.push_back(new TreeNode("on",174));
    lst.push_back(new TreeNode("for",157));
    lst.push_back(new TreeNode("His",138));
    lst.push_back(new TreeNode("are",124));
    lst.push_back(new TreeNode("be",123));

    TreeNode *l,*r;
    while(lst.size() > 1){
        //按照权值排序，使用插入排序
        for(auto i = lst.begin();i != lst.end();++i){
            auto j = i;
            ++j;
            for(;j!=lst.end();++j){
                if((*i)->weight > (*j)->weight){
                    TreeNode* t = *i;
                    *i = *j;
                    *j = t;
                }
            }
        }

        //排序完之后，都要取出前面2个元素
        l = lst.front();
        lst.pop_front();
        r = lst.front();
        lst.pop_front();
        TreeNode* n = new TreeNode("",l->weight + r->weight,l,r);  //再新建一个节点，左子树和右子树分别对应刚刚取出来的两个节点
        lst.push_back(n);  //重新放回list中
    }
    l = r = 0;  //指针使用之后需要置空
    TreeNode* t = lst.front();  //剩下的最后一个，就是哈夫曼树。
    cout << "Huffman Code:" << endl;
    printHuffmanCoding(t);
    cout << "Weighted path length:" << calcularLength(t) << endl;

    //程序运行完之后需要销毁二叉树
    destory(t);
    t = NULL;
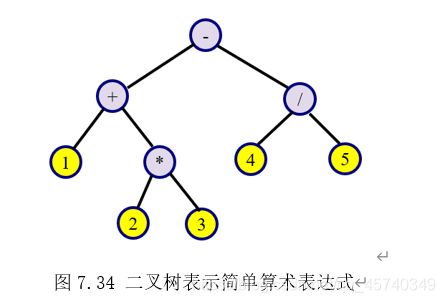
	return 0;
}

4、教材P248实验题8：简单算术表达式二叉树的构建和求值

编写一个程序exp7-8.cpp，先用二叉树来表示一个简单算术表达式，树的每一个结点包括一个运算符或运算数。在简单算术表达式中只包含+、-、、/和一位正整数且格式正确（不包括括号），并且要按照先乘除后加减的原则构造二叉树，图7.34所示为“1+23-4/5”代数表达式对应的二叉树，然后由对应的二叉树计算该表达式的值。

#include 
using namespace std;

struct TreeNode{
	int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode(int v){
        this->val = v;
        this->left = NULL;
        this->right = NULL;
    }
    TreeNode(char v,TreeNode* l,TreeNode *r){
        this->val = v;
        this->left = l;
        this->right = r;
    }
};

/*
string字符串转换成Int类型
*/
int stringToInt(string s){
	reverse(s.begin(),s.end());
	int res = 0;
	for(int i = 0;i<s.size();++i){
		res += (s[i]-'0') * pow(10,i);
	}
	return res;
}


/*
构造二叉树
*/
TreeNode* init(string s){
	if(s == ""){
		return NULL;
	}
	//首先找到+或者-
	int i = s.size() - 1;
	while(i>=0 && s[i] != '+' && s[i] != '-'){
		--i;
	}
	if(i >= 0){
		TreeNode* t = new TreeNode(s[i]);
		t->left = init(s.substr(0,i));
		t->right = init(s.substr(i+1));
		return t;
	}
	//找不到+-就找乘除
	i = s.size()-1;
	while(i>=0 && s[i] != '*' && s[i] != '/'){
		--i;
	}
	if(i >= 0){
		TreeNode* t = new TreeNode(s[i]);
		t->left = init(s.substr(0,i));
		t->right = init(s.substr(i+1));
		return t;
	}
	//找不到，则说明这是一个数值
	TreeNode* t = new TreeNode(stringToInt(s));
	return t;
}

/*
计算
*/
double calcular(TreeNode* t){
	if(!t){
		return 0;
	}
	double res = 0;
	if(t->left && t->right){
		//有左子树和右子树，说明当前表示一个符号
		switch (t->val){
		case '+':
			res = calcular(t->left) + calcular(t->right);
			break;
		case '-':
			res = calcular(t->left) - calcular(t->right);
			break;
		case '*':
			res = calcular(t->left) * calcular(t->right);
			break;
		case '/':
			res = calcular(t->left) * 1.0 / calcular(t->right);
			break;
		}
	}else{
		//没有左右子树（不可能会出现左子树不为空而右子树为空的情况）
		res = t->val;
	}
	return res;
}

/*
递归销毁二叉树
*/
void destory(TreeNode* node){
    if(node == NULL){
        return;  //已经为NULL，无需销毁
    }
    destory(node->left);
    destory(node->right);
    node->left = NULL; //销毁之后需要把指针置空
    node->right = NULL;
    delete node;
}

int main() {
	ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
	TreeNode* t = init("1+2*3-4/5");
	cout << "1+2*3-4/5 = " << calcular(t) << endl;
	TreeNode* t2 = init("1+2*3+36+10*3+25/6");
	cout << "1+2*3+36+10*3+25/6 = " << calcular(t2) << endl;
	
	destory(t);
	t = NULL;
	return 0;
}

教材P249实验题9：用二叉树表示家谱关系并实现各种查找功能

编写一个程序exp7-9.cpp，采用一棵二叉树表示一个家谱关系（由若干家谱记录构成，每个家谱记录由父亲、母亲和儿子的姓名构成，其中姓名是关键字），要求程序具有以下功能。
（1） 文件操作功能：家谱记录的输入，家谱记录的输出，清除全部文件记录和将家谱记录存盘。要求在输入家谱记录时按从祖先到子孙的顺序输入，第一个家谱记录的父亲域为所有人的祖先。
（2） 家谱操作功能：用括号表示法输出家谱二叉树，查找某人的所有儿子，查找某人的所有祖先（这里的祖先是指所设计的二叉树结构中某结点的所有祖先结点）。

#include 
using namespace std;
typedef long long ll;

typedef struct Node{
	string name; //姓名
	Node* left;  //左指针
	Node* right;  //右指针
	Node* parent;  //双亲
	bool isBoy;  //1男 0女
	Node(){
		name = "";
		left = NULL;
		right = NULL;
		parent = NULL;
		isBoy = 1;
	}
}TreeNode;
Node* root = NULL;
ifstream ifs;
ofstream ofs;
string a,b,c;

//根据文件内容建树
void init(TreeNode* &t,int depth = 1){
	
	t = new TreeNode();
	t->name = b;
	TreeNode* wife = 0;
	if(c != "."){
		//有妻子
		wife = new TreeNode();
		wife->name = c;
		wife->isBoy = 0;
		wife->parent = t;
		t->left = wife;
	}
	a = "";
	
	ifs >> a >> b >> c;	//继续读入3个数据
	if(ifs.eof()){   //如果读完了，就直接返回
		return;
	}
	if(a.size() == depth){ //辈分一样，说明是兄弟
		init(t->right,depth);  //递归建树
		t->right->parent = t;
	}else if(a.size() == depth + 1 && wife){
		//这是儿子
		init(wife->right,depth + 1);
		wife->right ->parent=wife;
	}else{
		//如果都不是，那么返回去给上一层
		return;
	}

	//上面递归return后的还剩下的a b c继续判断
	if(a.size() == depth){
		init(t->right,depth);
		t->right->parent = t;
	}
	
}

//括号法输出二叉树
void bracketingPrint(TreeNode* t = root){
	if(!t){
		return;
	}
	cout<<t->name;
	if(t->left || t->right){
		cout <<"(";
		bracketingPrint(t->left);
		if(t->right){
			cout << ",";
			bracketingPrint(t->right);
		}
		cout << ")";
	}
}

//根据名称寻找
TreeNode* findPeople(string name,TreeNode* t = root){
	if(!t){
		return 0;
	}
	if(t->name == name){
		return t;
	}
	TreeNode* n = findPeople(name,t->left);
	if(n){
		return n;	//如果在左边找到就返回左边的
	}
	return findPeople(name,t->right);	//否则返回右边的
}

//查找某人的所有儿子
void findAllChildren(string name){
	cout << "======================================" << endl;
	cout << "find all sons of " << name << endl;
	TreeNode* node = findPeople(name);
	if(!node){
		cout << "People "<< name <<" Not Found!!!" << endl;   //找不到这个人
		return;
	}
	if(node->isBoy){
		//如果是男的
		if(!(node->left)){
			cout << name << " is no wife!" << endl;   //他没有妻子
			return;
		}
		node = node->left;
	}
	//女的
	if(node->right){
		node = node->right;
		cout << "All the sons of "<< name <<" are as follows" << endl;
		while(node){
			cout << node->name << endl;
			node = node->right;
		}
	}else{
		//没有儿子
		cout << name << " is no sons!" << endl;
	}
}

void findAllAncestors(string name){
	cout << "======================================" << endl;
	cout << "find all ancestors of " << name << endl;
	TreeNode* node = findPeople(name);
	if(!node){
		cout << "People "<< name <<" Not Found!!!" << endl;   //找不到这个人
		return;
	}
	if(!node->isBoy){
		//女，与祖先们不构成血缘关系，忽略
		cout <<  name <<" is not a men!!!" << endl;
		return;
	}
	cout << "All ancestors of "<<name<<" are as follows:" << endl;
	node = node->parent;  
	while(node){
		if(!node->isBoy){
			cout << node->name << endl;
			node = node->parent;
			cout << node->name << endl;
		}
		node = node->parent;   //一直往上寻找
	}
}

/*
输出家谱
*/
void printGenealogy(TreeNode* t = root,int depth = 0){
	if(!t){
		return;
	}
	cout << string(depth + 1,'#') << " " << t->name << " ";
	if(t->left){
		cout << t->left->name<< endl;
		printGenealogy(t->left->right,depth + 1);
	}else{
		cout << "." << endl;
	}
	printGenealogy(t->right,depth);
}
/*
输出家谱到文件
*/
void printGenealogyToFile(TreeNode* t = root,int depth = 0){
	if(!t || !ofs.is_open()){
		return;
	}
	ofs << string(depth + 1,'#') << " " << t->name << " ";
	if(t->left){
		ofs << t->left->name<< endl;
		printGenealogyToFile(t->left->right,depth + 1);
	}else{
		ofs << "." << endl;
	}
	printGenealogyToFile(t->right,depth);
}

/*
销毁二叉树
*/
void destory(TreeNode* node = root){
    if(node == NULL){
        return;  //已经为NULL，无需销毁
    }
    destory(node->left);
    destory(node->right);
    node->left = NULL; //销毁之后需要把指针置空
    node->right = NULL;
    delete node;
}

int main() {
	ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
	ifs.open("DS Science\\02-05\\data.txt",ios::in); //打开data.txt文件
	ifs >> a >> b >> c;    //读入文件里面的3个数据
	init(root);			//递归建树
	ifs.close();   //使用完成后要关闭流
	bracketingPrint();   //括号法输出
	cout << endl;
	findAllChildren("zhangsan");   //查找zhangsan的所有儿子
	findAllChildren("lujiajing");   //查找lujiajing的所有儿子
	findAllChildren("zhangsansanyi");   //查找所有儿子
	findAllChildren("wodian");   //查找所有儿子
	findAllAncestors("zhangsansanyi");   //查找他的所有祖先
	findAllAncestors("daoweizhi");   //查找他的所有祖先
	cout << "Output genealogy" << endl; // 输出家谱
	printGenealogy();
	//输出家谱到文件
	ofs.open("DS Science\\02-05\\data1.txt",ios::out);
	cout << "Output genealogy to file" << endl; // 输出家谱到文件
	printGenealogyToFile();
	destory();  //销毁二叉树
	root = 0;   //置空
	return 0;
}