机器学习系列笔记九: 逻辑回归
机器学习系列笔记九: 逻辑回归
文章目录
- 机器学习系列笔记九: 逻辑回归
-
- Intro
- Logistic Regression原理
-
- 激活函数
- 逻辑回归的损失函数
- 实现逻辑回归算法
- 决策边界
- 在逻辑回归中使用多项式特征
-
- 代码实现
- 逻辑回归中使用正则化
-
- scikit-learn中的逻辑回归
- 二分类算法改进作用于多分类问题
-
- 代码实现
-
- OvO/OvR作为参数传入二分类算法
- OvR/OvO作为类,二分类算法作为参数
- 总结
- 参考致谢
Intro
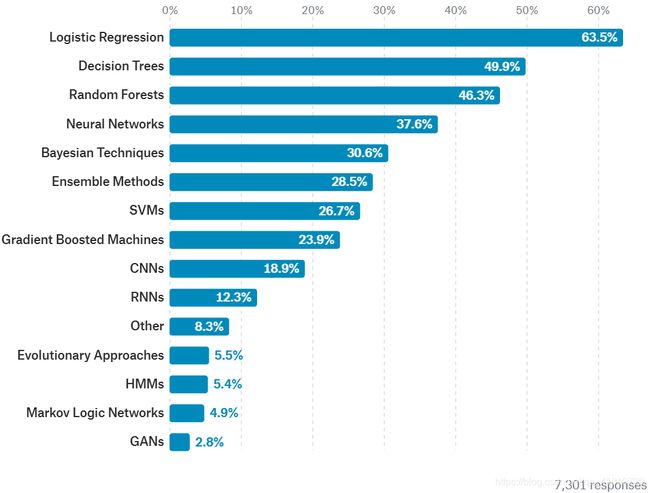
为了说明逻辑回归的重要性,先post一张图:
这是kaggle在2017年对工作最常用的数据科学方法的排名统计,可以看到逻辑回归LogicRegression是各个行业中(除了军事和安全领域)最为常用的数据科学方法。这也说明对于机器学习算法并不见得是越复杂越好的,要根据实际的使用场景选择最合适的算法。
没有免费午餐定理:并没有哪个算法比哪个算法更好,只是在特定的场景中的效果有差别。
那么逻辑回归是什么?其实如果修过吴恩达的机器学习课程的同学都不陌生,在此做一个系统的总结。
首先明确一个容易混淆的概念:逻辑回归是解决二分类问题的。
Logistic Regression原理
逻辑回归的原理是将样本特征和样本发生的概率联系起来,由于概率是一个数,所以称之为回归,然后会根据这个发生概率是否高于阈值(p=0.5)来把结果划分为0,1两个固定的结果(类别),所以解决的是一个二分类问题。
假设通过回归计算得出的结果 y ^ \hat{y} y^是一个数,为了将之转换为概率我们通常需要在回归的结果上通过一个激活函数(比如sigmoid)使之映射到0~1区间。
σ ( y ^ ) = > p ^ ∈ ( 0 , 1 ) \sigma(\hat{y})=>\hat{p}\in(0,1) σ(y^)=>p^∈(0,1)
然后通过判断 p ^ \hat{p} p^ (该样本发生的概率)是否在50%以上做一个划分
y ^ = { 0 p ^ < 0.5 1 p ^ > 0.5 \hat{y}=\begin{cases} 0& \hat{p}<0.5\\ 1& \hat{p}>0.5\\ \end{cases} y^={01p^<0.5p^>0.5
所以最终结果就变为了类别0或者类别1这样的结果。
逻辑回归就是在线性回归的基础上通过激活函数把结果映射为概率值
激活函数
在逻辑回归中,如何寻找合适的激活函数将回归结果映射为概率就成为了一个重要问题,通常可以采用sigmoid函数作为激活函数 σ ( t ) \sigma(t) σ(t):
σ ( t ) = 1 1 + e − t \sigma(t)=\frac{1}{1+e^{-t}} σ(t)=1+e−t1
该函数的图像如下:
可以看到这个函数的值域是(0,1),这符合概率的值域,当t>0时,p>0.5,t<0则p<0.5.所以分界点就是t=0.
考虑将线性回归的结果带入t中可以得出一个结论:在使用sigmoid函数处理线性回归结果之前,我们需要将回归结果进行标准化处理,使之均值为0,而这个0就是所谓的决策边界。
逻辑回归的损失函数
不同于线性回归中所采用的损失函数 M S E = ( y ^ − y ) 2 MSE=(\hat{y}-y)^2 MSE=(y^−y)2 ,对于逻辑回归,因为其最终结果非0即1,所以要对损失函数的定义进行一个转换(这里有一点绕,需要在逻辑上进行一个类比):
然后,我们希望通过一个函数来表达这样的一个损失cost:
cos t = { − log ( p ^ ) i f y = 1 − log ( 1 − p ^ ) i f y = 0 \cos t=\begin{cases} -\log \left( \hat{p} \right)& if\ \ y=1\\ -\log \left( 1-\hat{p} \right)& if\ \ y=0\\ \end{cases} cost={−log(p^)−log(1−p^)if y=1if y=0

将上式稍作修改就变成了如下形式:
cos t = − y log ( p ^ ) − ( 1 − y ) log ( 1 − p ^ ) \cos t=-y\log \left( \hat{p} \right) -\left( 1-y \right) \log \left( 1-\hat{p} \right) cost=−ylog(p^)−(1−y)log(1−p^)
进而最终对于逻辑回归的损失函数定义如下:
J ( θ ) = − 1 m ∑ i m y ( i ) log ( p ^ ( i ) ) − ( 1 − y ( i ) ) log ( 1 − p ^ ( i ) ) J\left( \theta \right) =-\frac{1}{m}\sum_i^m{y^{\left( i \right)}}\log \left( \hat{p}^{\left( i \right)} \right) -\left( 1-y^{\left( i \right)} \right) \log \left( 1-\hat{p}^{\left( i \right)} \right) J(θ)=−m1i∑my(i)log(p^(i))−(1−y(i))log(1−p^(i))
- y ( i ) y^{(i)} y(i) 表示第i个样本的真实分类
- p ^ ( i ) = σ ( X b i θ ) \hat{p}^{(i)}=\sigma(X_b^{i}\theta) p^(i)=σ(Xbiθ) 表示对于第i个样本模型的预测结果。
由于大多数激活函数非线性,所以对于逻辑回归的损失函数是没有公式解的,只能用梯度下降法求解。而对于该损失函数的梯度求解结果如下:
J ( θ ) θ j = 1 m ∑ i = 1 m ( σ ( X b ( i ) θ ) − y ( i ) ) X j ( i ) \frac{J\left( \theta \right)}{\theta _j}=\frac{1}{m}\sum_{i=1}^m{\left( \sigma \left( X_{b}^{\left( i \right)}\theta \right) -y^{\left( i \right)} \right) X_{j}^{\left( i \right)}} θjJ(θ)=m1i=1∑m(σ(Xb(i)θ)−y(i))Xj(i)
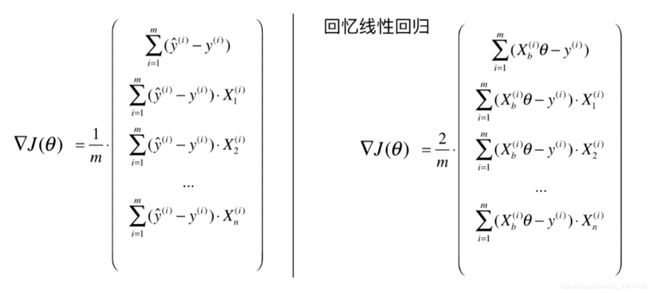
向量化梯度:
∇ J ( θ ) = 1 m ⋅ X b T ⋅ ( σ ( X b θ ) − y ) \nabla J\left( \theta \right) =\frac{1}{m}\cdot X_{b}^{T}\cdot \left( \sigma \left( X_b\theta \right) -y \right) ∇J(θ)=m1⋅XbT⋅(σ(Xbθ)−y)
实现逻辑回归算法
import numpy as np
from sklearn.metrics import accuracy_score
class LogicRegression:
def __init__(self):
"""初始化Logic Regression 模型"""
self.coef_ = None
self.intercept_ = None
self._theta = None
def _sigmoid(self, t):
return 1 / (1 + np.exp(-t))
def fit(self, X_train, y_train, eta=0.01, n_iters=1e4):
"""根据训练数据集X_train,y_train,使用梯度下降法训练逻辑回归模型"""
assert X_train.shape[0] == y_train.shape[0], \
"the row-size of X_train must be equal to y_train"
def J(theta, X_b, y):
y_hat = self._sigmoid(X_b.dot(theta))
try:
return np.sum(y * np.log(y_hat) + (1 - y) * np.log(1 - y_hat)) / len(y)
except:
return float("inf")
def dJ(theta, X_b, y):
return X_b.T.dot(self._sigmoid(X_b.dot(theta)) - y) / len(X_b)
def gradient_descent(X_b, y, initial_theta, eta, n_iters=1e4, epsilon=1e-8):
theta = initial_theta
cur_iter = 0
while cur_iter < n_iters:
gradient = dJ(theta, X_b, y)
last_theta = theta
theta = theta - eta * gradient
if (abs(J(theta, X_b, y) - J(last_theta, X_b, y)) < epsilon):
break
cur_iter += 1
return theta
X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
initial_theta = np.zeros(X_b.shape[1])
self._theta = gradient_descent(X_b, y_train, initial_theta, eta, n_iters)
self.coef_ = self._theta[1:]
self.intercept_ = self._theta[0]
return self
def predict_proba(self,X_predict):
X_b = np.hstack([np.ones((len(X_predict), 1)), X_predict])
return self._sigmoid(X_b.dot(self._theta))
def predict(self,X_predict):
proba = self.predict_proba(X_predict)
return np.array(proba >=0.5,dtype=np.int)
def score(self,X_test,y_test):
y_predict = self.predict(X_test)
return accuracy_score(y_test,y_predict)
def __repr__(self):
return "LogisticRegression()"
使用鸢尾花数据集测试逻辑回归
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
iris = datasets.load_iris()
X = iris.data
y = iris.target
# 因为实现的逻辑回归暂时只能解决二分类问题,所以将数据处理为两类
X = X[y<2,:2]
y = y[y<2]
X.shape
(100, 2)
y.shape
(100,)
plt.scatter(X[y==0,0],X[y==0,1],color='red')
plt.scatter(X[y==1,0],X[y==1,1],color='blue')
plt.show()
使用逻辑回归
from relatedCode.LogicRegression import LogicRegression
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(X,y,random_state=666)
log_reg = LogicRegression()
log_reg.fit(X_train,y_train)
log_reg.score(X_test,y_test)
1.0
可以看到逻辑回归的分类效果还是相当不错的
log_reg.predict_proba(X_test)
array([0.93292947, 0.98717455, 0.15541379, 0.01786837, 0.03909442,
0.01972689, 0.05214631, 0.99683149, 0.98092348, 0.75469962,
0.0473811 , 0.00362352, 0.27122595, 0.03909442, 0.84902103,
0.80627393, 0.83574223, 0.33477608, 0.06921637, 0.21582553,
0.0240109 , 0.1836441 , 0.98092348, 0.98947619, 0.08342411])
log_reg.predict(X_test)
array([1, 1, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0,
1, 1, 0])
决策边界
在前面Intro中提到,对于使用sigmoid函数作为激活函数的逻辑回归模型,其决策边界为0,即
θ T ⋅ x b = 0 \theta^T \cdot x_b=0 θT⋅xb=0
如果X有两个特征: θ 0 + θ 1 x 1 + θ 2 x 2 = 0 \theta_0+\theta_1x_1+\theta_2x_2=0 θ0+θ1x1+θ2x2=0,则可以求出两个特征之间的等式:
x 2 = − θ 0 − θ 1 x 1 θ 2 x_2 = \frac{-\theta_0-\theta_1x_1}{\theta_2} x2=θ2−θ0−θ1x1
def x2(x1):
return (-log_reg.coef_[0]*x1-log_reg.intercept_)/log_reg.coef_[1]
x1_plot = np.linspace(4,8,1000)
x2_plot = x2(x1_plot)
plt.plot(x1_plot,x2_plot)
plt.scatter(X[y==0,0],X[y==0,1],color='red')
plt.scatter(X[y==1,0],X[y==1,1],color='blue')
plt.show()
可以看到,求出来的决策边界大体上将数据分为了红蓝两方,如果新送入逻辑回归模型的数据位于这条决策边界的上方则归类为0,下方则分类为1
接下来为方便测试,将绘制决策边界封装为一个方法:
def plot_decision_boundary(model, axis):
x0, x1 = np.meshgrid(
np.linspace(axis[0], axis[1], int((axis[1]-axis[0])*100)).reshape(-1, 1),
np.linspace(axis[2], axis[3], int((axis[3]-axis[2])*100)).reshape(-1, 1),
)
X_new = np.c_[x0.ravel(), x1.ravel()]
y_predict = model.predict(X_new)
zz = y_predict.reshape(x0.shape)
from matplotlib.colors import ListedColormap
custom_cmap = ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
plt.contourf(x0, x1, zz, linewidth=5, cmap=custom_cmap)
import warnings
warnings.filterwarnings("ignore")
plot_decision_boundary(log_reg, axis=[4, 7.5, 1.5, 4.5])
plt.scatter(X[y==0,0], X[y==0,1])
plt.scatter(X[y==1,0], X[y==1,1])
plt.show()
借此,我们看看KNN算法的决策边界是什么
from sklearn.neighbors import KNeighborsClassifier
knn_clf = KNeighborsClassifier()
knn_clf.fit(X_train,y_train)
KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',
metric_params=None, n_jobs=None, n_neighbors=5, p=2,
weights='uniform')
knn_clf.score(X_test,y_test)
1.0
plot_decision_boundary(knn_clf, axis=[4, 7.5, 1.5, 4.5])
plt.scatter(X[y==0,0], X[y==0,1])
plt.scatter(X[y==1,0], X[y==1,1])
plt.show()
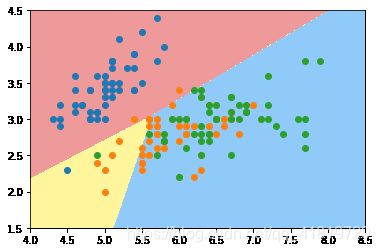
在此基础上,我们看看对于有三个分类的鸢尾花原始数据,KNN的决策边界是什么样的
knn_clf_all = KNeighborsClassifier()
knn_clf_all.fit(iris.data[:,:2],iris.target)
KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',
metric_params=None, n_jobs=None, n_neighbors=5, p=2,
weights='uniform')
plot_decision_boundary(knn_clf_all,axis=[4,8,1.5,4.5])
plt.scatter(iris.data[iris.target==0,0],iris.data[iris.target==0,1])
plt.scatter(iris.data[iris.target==1,0],iris.data[iris.target==1,1])
plt.scatter(iris.data[iris.target==2,0],iris.data[iris.target==2,1])
plt.show()
可以看到黄蓝之间的决策边界十分不规则,这是过拟合的现象,对于KNN算法而言,定义的n_neighbors越小,模型越复杂,模型越复杂就越容易出现过拟合,所以我们设置n_neighbors=50,再绘制一次决策边界
knn_clf_all = KNeighborsClassifier(n_neighbors=50)
knn_clf_all.fit(iris.data[:,:2],iris.target)
plot_decision_boundary(knn_clf_all,axis=[4,8,1.5,4.5])
plt.scatter(iris.data[iris.target==0,0],iris.data[iris.target==0,1])
plt.scatter(iris.data[iris.target==1,0],iris.data[iris.target==1,1])
plt.scatter(iris.data[iris.target==2,0],iris.data[iris.target==2,1])
plt.show()
在逻辑回归中使用多项式特征
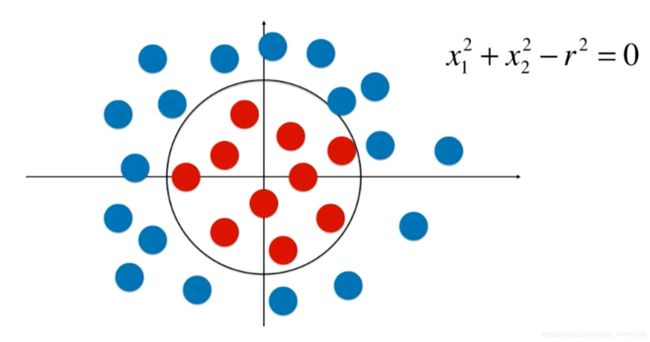
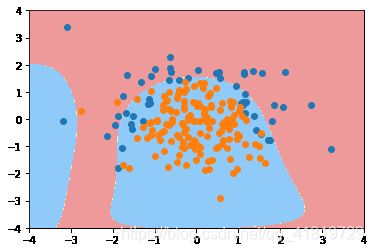
根据前面的推导与验证,我们发现,对于逻辑回归,其内部实现的线性回归算法导致其拟合的决策边界是一条直线,而且对于非线性分布的数据分类效果就会大打折扣,如下图的数据分布:
那么有没有办法可以解决逻辑回归的这个问题呢?那就是前面学到过的使用多项式特征来改进线性回归算法,使得逻辑回归的内部回归算法为多项式回归。
代码实现
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(666)
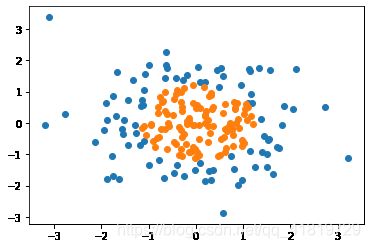
X = np.random.normal(0,1,size=(200,2))
y = np.array((X[:,0]**2+X[:,1]**2)<1.5,dtype=int)
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()
接下来使用逻辑回归来对上面的数据进行分类
from relatedCode.LogicRegression import LogicRegression
logic_reg = LogicRegression()
logic_reg.fit(X,y)
logic_reg.score(X,y)
0.605
可以看到这个分类的准确度是比较低的
import warnings
warnings.filterwarnings("ignore")
def plot_decision_boundary(model, axis):
x0, x1 = np.meshgrid(
np.linspace(axis[0], axis[1], int((axis[1]-axis[0])*100)).reshape(-1, 1),
np.linspace(axis[2], axis[3], int((axis[3]-axis[2])*100)).reshape(-1, 1),
)
X_new = np.c_[x0.ravel(), x1.ravel()]
y_predict = model.predict(X_new)
zz = y_predict.reshape(x0.shape)
from matplotlib.colors import ListedColormap
custom_cmap = ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
plt.contourf(x0, x1, zz, linewidth=5, cmap=custom_cmap)
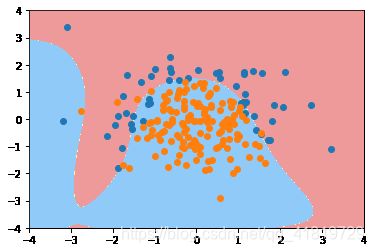
plot_decision_boundary(logic_reg,axis=[-4,4,-4,4])
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()
可以看到没有添加多项式特征的逻辑回归使用了一条直线来对特征空间进行划分,结果不尽人意
接下来我们通过使用pipline为逻辑回归添加多项式特征
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.preprocessing import StandardScaler
def PolynomialLogisticRegression(degree):
return Pipeline([
('poly',PolynomialFeatures(degree=degree)),
('std_scaler',StandardScaler()),
('logic_regression',LogicRegression())
])
poly_log_reg = PolynomialLogisticRegression(degree=2)
poly_log_reg.fit(X,y)
Pipeline(memory=None,
steps=[('poly',
PolynomialFeatures(degree=2, include_bias=True,
interaction_only=False, order='C')),
('std_scaler',
StandardScaler(copy=True, with_mean=True, with_std=True)),
('logic_regression', LogisticRegression())],
verbose=False)
我们看看此时的分类准确度
poly_log_reg.score(X,y)
0.95
绘制决策边界
plot_decision_boundary(poly_log_reg,axis=[-4,4,-4,4])
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()
如果特征项添加过多,也会出现过拟合的情况
poly_log_reg2 = PolynomialLogisticRegression(degree=20)
poly_log_reg2.fit(X,y)
plot_decision_boundary(poly_log_reg2,axis=[-4,4,-4,4])
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()
为解决这种过拟合的情况,在前面多项式回归的总结中有总结两种方案:
- 减少特征(PCA),降低模型复杂度
- 使用模型正则化
逻辑回归中使用正则化
在多项式回归中对模型正则化做了一系列阐述,其本质就是通过在原本损失函数上添加L1/L2子项,在损失函数最小化的同时使得模型参数也跟着缩小。
C ⋅ J ( θ ) + L 1 C\cdot J(\theta)+L1 C⋅J(θ)+L1
C ⋅ J ( θ ) + L 2 C\cdot J(\theta)+L2 C⋅J(θ)+L2
- Ridge Regression中损失函数的附加项 ∑ i = 1 n ( θ i ) 2 \sum^n_{i=1}(\theta_i)^2 ∑i=1n(θi)2 也称之为
L2正则项 - LASSO Regression中损失函数的附加项 ∑ i = 1 n ∣ θ i ∣ \sum^n_{i=1}|\theta_i| ∑i=1n∣θi∣ 也称之为
L1正则项
在scikit-learn中非常推崇使用模型正则化的方式对避免模型过拟合。
接下来,我们就通过使用scikit-learn所提供的API来实现逻辑回归模型的正则化
scikit-learn中的逻辑回归
首先模拟数据
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(666)
X = np.random.normal(0,1,size=(200,2))
y = np.array((X[:,0]**2+X[:,1])<1.5,dtype=int)
# 增加噪声
for _ in range(20):
y[np.random.randint(200)]=1
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()
分割数据集
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(X,y,random_state=666)
使用scikit learn中的逻辑回归
import warnings
warnings.filterwarnings("ignore")
from sklearn.linear_model import LogisticRegression
log_reg = LogisticRegression()
log_reg.fit(X_train,y_train)
LogisticRegression(C=1.0, class_weight=None, dual=False, fit_intercept=True,
intercept_scaling=1, l1_ratio=None, max_iter=100,
multi_class='warn', n_jobs=None, penalty='l2',
random_state=None, solver='warn', tol=0.0001, verbose=0,
warm_start=False)
log_reg.score(X_test,y_test)
0.86
可视化决策边界
def plot_decision_boundary(model, axis):
x0, x1 = np.meshgrid(
np.linspace(axis[0], axis[1], int((axis[1]-axis[0])*100)).reshape(-1, 1),
np.linspace(axis[2], axis[3], int((axis[3]-axis[2])*100)).reshape(-1, 1),
)
X_new = np.c_[x0.ravel(), x1.ravel()]
y_predict = model.predict(X_new)
zz = y_predict.reshape(x0.shape)
from matplotlib.colors import ListedColormap
custom_cmap = ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
plt.contourf(x0, x1, zz, linewidth=5, cmap=custom_cmap)
plot_decision_boundary(log_reg,axis=[-4,4,-4,4])
plt.scatter(X[y==0,0], X[y==0,1])
plt.scatter(X[y==1,0], X[y==1,1])
plt.show()
使用多项式逻辑回归
from sklearn.preprocessing import PolynomialFeatures
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline
def PolymialLogicRegression(degree):
return Pipeline([
('poly',PolynomialFeatures(degree=degree)),
('std_scaler',StandardScaler()),
('logistic_regression',LogisticRegression())
])
poly_reg = PolymialLogicRegression(degree=2)
poly_reg.fit(X_train,y_train)
Pipeline(memory=None,
steps=[('poly',
PolynomialFeatures(degree=2, include_bias=True,
interaction_only=False, order='C')),
('std_scaler',
StandardScaler(copy=True, with_mean=True, with_std=True)),
('logistic_regression',
LogisticRegression(C=1.0, class_weight=None, dual=False,
fit_intercept=True, intercept_scaling=1,
l1_ratio=None, max_iter=100,
multi_class='warn', n_jobs=None,
penalty='l2', random_state=None,
solver='warn', tol=0.0001, verbose=0,
warm_start=False))],
verbose=False)
poly_reg.score(X_test,y_test)
0.94
可视化决策边界
plot_decision_boundary(poly_reg, axis=[-4, 4, -4, 4])
plt.scatter(X[y==0,0], X[y==0,1])
plt.scatter(X[y==1,0], X[y==1,1])
plt.show()
增加样本特征(more degree)
poly_reg2 = PolymialLogicRegression(degree=20)
poly_reg2.fit(X_train,y_train)
poly_reg2.score(X_test,y_test)
0.92
plot_decision_boundary(poly_reg2, axis=[-4, 4, -4, 4])
plt.scatter(X[y==0,0], X[y==0,1])
plt.scatter(X[y==1,0], X[y==1,1])
plt.show()
在scikit-learn提供的logisticRegression提供了参数C来进行模型的正则化
class sklearn.linear_model.LogisticRegression(penalty='l2', *, dual=False, tol=0.0001, C=1.0, fit_intercept=True, intercept_scaling=1, class_weight=None, random_state=None, solver='lbfgs', max_iter=100, multi_class='auto', verbose=0, warm_start=False, n_jobs=None, l1_ratio=None)
C float, default=1.0
Inverse of regularization strength; must be a positive float. Like in support vector machines, smaller values specify stronger regularization.
正则化强度的倒数;必须是正浮点数。和支持向量机一样,较小的值表示正则化更强。
def PolynomialLogisticRegression_C(degree,C):
return Pipeline([
('poly',PolynomialFeatures(degree=degree)),
('std_scaler',StandardScaler()),
('logistic_regression',LogisticRegression(C=C))
])
poly_reg3 = PolynomialLogisticRegression_C(degree=20,C=0.1)
poly_reg3.fit(X_train,y_train)
Pipeline(memory=None,
steps=[('poly',
PolynomialFeatures(degree=20, include_bias=True,
interaction_only=False, order='C')),
('std_scaler',
StandardScaler(copy=True, with_mean=True, with_std=True)),
('logistic_regression',
LogisticRegression(C=0.1, class_weight=None, dual=False,
fit_intercept=True, intercept_scaling=1,
l1_ratio=None, max_iter=100,
multi_class='warn', n_jobs=None,
penalty='l2', random_state=None,
solver='warn', tol=0.0001, verbose=0,
warm_start=False))],
verbose=False)
poly_reg3.score(X_train,y_train)
0.8533333333333334
poly_reg3.score(X_test,y_test)
0.92
plot_decision_boundary(poly_reg3, axis=[-4, 4, -4, 4])
plt.scatter(X[y==0,0], X[y==0,1])
plt.scatter(X[y==1,0], X[y==1,1])
plt.show()
penalty {‘l1’, ‘l2’, ‘elasticnet’, ‘none’}, default=’l2’
Used to specify the norm used in the penalization. The ‘newton-cg’, ‘sag’ and ‘lbfgs’ solvers support only l2 penalties. ‘elasticnet’ is only supported by the ‘saga’ solver. If ‘none’ (not supported by the liblinear solver), no regularization is applied.
指定模型正则化使用的附加项
def PolynomialLogisticRegression_penalty(degree,C,penalty='l2'):
return Pipeline([
('poly',PolynomialFeatures(degree=degree)),
('std_scaler',StandardScaler()),
('log_reg',LogisticRegression(penalty=penalty))
])
poly_reg4 = PolynomialLogisticRegression_penalty(degree=20,C=0.1,penalty='l1')
poly_reg4.fit(X_train,y_train)
Pipeline(memory=None,
steps=[('poly',
PolynomialFeatures(degree=20, include_bias=True,
interaction_only=False, order='C')),
('std_scaler',
StandardScaler(copy=True, with_mean=True, with_std=True)),
('log_reg',
LogisticRegression(C=1.0, class_weight=None, dual=False,
fit_intercept=True, intercept_scaling=1,
l1_ratio=None, max_iter=100,
multi_class='warn', n_jobs=None,
penalty='l1', random_state=None,
solver='warn', tol=0.0001, verbose=0,
warm_start=False))],
verbose=False)
poly_reg4.score(X_train,y_train)
0.94
poly_reg4.score(X_test,y_test)
0.94
plot_decision_boundary(poly_reg4, axis=[-4, 4, -4, 4])
plt.scatter(X[y==0,0], X[y==0,1])
plt.scatter(X[y==1,0], X[y==1,1])
plt.show()
二分类算法改进作用于多分类问题
为了使得以逻辑回归为首的二分类算法可以用于多分类问题的解决,通常可以采用两种手段来实现:
- OvR(One vs Rest)
- OvO(One vs One)
OvR
OvO
代码实现
import numpy as np
import matplotlib.pyplot as plt
import warnings
from sklearn import datasets
from sklearn.model_selection import train_test_split
warnings.filterwarnings("ignore")
iris = datasets.load_iris()
X = iris.data[:,:2]
y = iris.target
X_train,X_test,y_train,y_test = train_test_split(X,y,random_state=666)
OvO/OvR作为参数传入二分类算法
scikit-learn的LogisticRegression为我们实现了OvO与OvR,默认为OvR模式
multi_class {‘auto’, ‘ovr’, ‘multinomial’}, default=’auto’
If the option chosen is ‘ovr’, then a binary problem is fit for each label. For ‘multinomial’ the loss minimised is the multinomial loss fit across the entire probability distribution, even when the data is binary. ‘multinomial’ is unavailable when solver=’liblinear’. ‘auto’ selects ‘ovr’ if the data is binary, or if solver=’liblinear’, and otherwise selects ‘multinomial’.
New in version 0.18: Stochastic Average Gradient descent solver for ‘multinomial’ case.
Changed in version 0.22: Default changed from ‘ovr’ to ‘auto’ in 0.22.
from sklearn.linear_model import LogisticRegression
log_reg = LogisticRegression()
log_reg.fit(X_train,y_train)
LogisticRegression(C=1.0, class_weight=None, dual=False, fit_intercept=True,
intercept_scaling=1, l1_ratio=None, max_iter=100,
multi_class='warn', n_jobs=None, penalty='l2',
random_state=None, solver='warn', tol=0.0001, verbose=0,
warm_start=False)
log_reg.score(X_test,y_test)
0.6578947368421053
def plot_decision_boundary(model, axis):
x0, x1 = np.meshgrid(
np.linspace(axis[0], axis[1], int((axis[1]-axis[0])*100)).reshape(-1, 1),
np.linspace(axis[2], axis[3], int((axis[3]-axis[2])*100)).reshape(-1, 1),
)
X_new = np.c_[x0.ravel(), x1.ravel()]
y_predict = model.predict(X_new)
zz = y_predict.reshape(x0.shape)
from matplotlib.colors import ListedColormap
custom_cmap = ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
plt.contourf(x0, x1, zz, linewidth=5, cmap=custom_cmap)
plot_decision_boundary(log_reg,axis=[4,8.5,1.5,4.5])
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.scatter(X[y==2,0],X[y==2,1])
plt.show()
通过OvO改进逻辑分类
log_reg2 = LogisticRegression(multi_class='multinomial',solver='newton-cg')
log_reg2.fit(X_train,y_train)
log_reg2.score(X_test,y_test)
0.7894736842105263
plot_decision_boundary(log_reg2,axis=[4,8.5,1.5,4.5])
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.scatter(X[y==2,0],X[y==2,1])
plt.show()
使用数据的所有特征看看分类的结果
X = iris.data
y = iris.target
X_train,X_test,y_train,y_test = train_test_split(X,y,random_state = 666)
OvR的方式
log_reg = LogisticRegression()
log_reg.fit(X_train,y_train)
log_reg.score(X_test,y_test)
0.9473684210526315
OvO的方式
log_reg2 = LogisticRegression(multi_class='multinomial',solver='newton-cg')
log_reg2.fit(X_train,y_train)
log_reg2.score(X_test,y_test)
1.0
使用手写数据集测试分类的结果
准备数据
from sklearn.datasets import fetch_mldata
mnist = fetch_mldata("MNIST original")
mnist
{'DESCR': 'mldata.org dataset: mnist-original',
'COL_NAMES': ['label', 'data'],
'target': array([0., 0., 0., ..., 9., 9., 9.]),
'data': array([[0, 0, 0, ..., 0, 0, 0],
[0, 0, 0, ..., 0, 0, 0],
[0, 0, 0, ..., 0, 0, 0],
...,
[0, 0, 0, ..., 0, 0, 0],
[0, 0, 0, ..., 0, 0, 0],
[0, 0, 0, ..., 0, 0, 0]], dtype=uint8)}
X,y = mnist['data'],mnist['target']
X.shape
(70000, 784)
X_train = np.array(X[:6000],dtype=float)
y_train = np.array(y[:6000],dtype=float)
X_test = np.array(X[6000:7000],dtype=float)
y_test = np.array(y[6000:7000],dtype=float)
from sklearn.decomposition import PCA
pca = PCA(0.9)
pca.fit(X_train)
X_train_reduction = pca.transform(X_train)
X_test_reduction = pca.transform(X_test)
X_train_reduction.shape
(6000, 62)
使用默认OvR的方式
%%time
log_reg = LogisticRegression()
log_reg.fit(X_train_reduction,y_train)
log_reg.score(X_test_reduction,y_test)
Wall time: 944 ms
0.988
使用OvO的方式
%%time
log_reg2 = LogisticRegression(multi_class='multinomial',solver='newton-cg')
log_reg2.fit(X_train_reduction,y_train)
log_reg2.score(X_test_reduction,y_test)
Wall time: 1.87 s
0.991
OvR/OvO作为类,二分类算法作为参数
%%time
from sklearn.multiclass import OneVsRestClassifier
ovr = OneVsRestClassifier(log_reg)
ovr.fit(X_train_reduction,y_train)
ovr.score(X_test_reduction,y_test)
Wall time: 972 ms
0.988
%%time
from sklearn.multiclass import OneVsOneClassifier
ovo = OneVsOneClassifier(log_reg)
ovo.fit(X_train_reduction,y_train)
ovo.score(X_test_reduction,y_test)
Wall time: 866 ms
0.988
总结
参考致谢
liuyubobo:https://github.com/liuyubobobo/Play-with-Machine-Learning-Algorithms
liuyubobo:https://coding.imooc.com/class/169.html
莫烦Python:https://www.bilibili.com/video/BV1xW411Y7Qd?from=search&seid=11773783205368546023
吴恩达机器学习:https://zh.coursera.org/learn/machine-learning