算法-二叉树-简单-二叉树的直径、将有序数组转换成二叉搜索树

记录一下算法题的学习9

二叉树的直径

题目：给你一棵二叉树的根节点，返回该树的 直径 。

二叉树的 直径 是指树中任意两个节点之间最长路径的 长度 。这条路径可能经过也可能不经过根节点 root 。两节点之间路径的 长度 由它们之间边数表示

读完题目，我们很容易联系到我们做过的二叉树的最大深度

算法-二叉树-简单-二叉树的最大和最小深度-CSDN博客

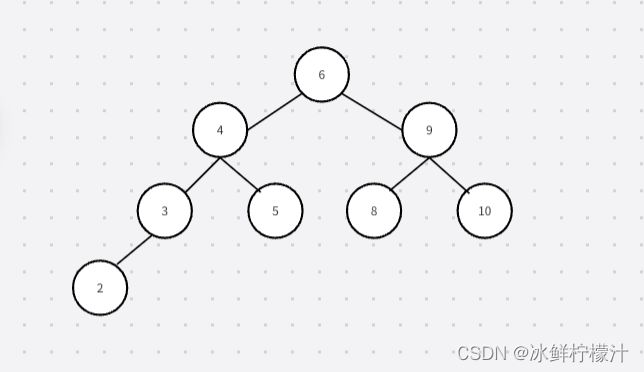
举例视图，便于观察

 由图可知：我们现在先求左子树的最大深度（加上根节点），即[6,4,3,2]----->4,而右子树的最大深度（加上根节点）为[6,9,10]or[6,9,8]---->3,但是这是最大深度是最多节点数，直径是树中任意两个节点之间最长路径的长度，即2和10 或者 2和8之间的连线边数，所以是右子树的最大深度+左子树的最大深度-2得到最长路径

 

这张图就是左子树深度[6,4,3,2]-->4,右子树深度[6]-->1(这是算上了根节点)，右子树的最大深度+左子树的最大深度-2得到最长路径 即3

 深度优先搜索代码展示：

//这道题很容易联想到二叉树的最大深度这道题目，我们现在就需要求二叉树的最大深度,在去求直径
class Solution {
     int ans=0;
      public int maxDepth(TreeNode node) {
        //访问到空节点，返回0
       if(node==null){
           return 0;
       }
       int leftDepth=maxDepth(node.left)+1; //得到根节点root左子树的最长路径上的节点数
       int rightDepth=maxDepth(node.right)+1;//得到根节点root右子树的最长路径上的节点数
       ans=Math.max(ans,leftDepth+rightDepth-2);//这里的思考关键： 二叉树的直径就是左子树的最多节点数+右子树上的最多节点数-2
      return Math.max(leftDepth,rightDepth);
    }
    public int diameterOfBinaryTree(TreeNode root) {
        maxDepth(root);
        return ans;//最长路径
}

     
}

将有序数组转换成二叉搜索树

题目：

给你一个整数数组 nums ，其中元素已经按 升序 排列，请你将其转换为一棵 高度平衡 二叉搜索树。  

高度平衡 二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 」的二叉树。

 题目分析：根据数组 元素升序排列，我们可以想到二叉树的中序遍历顺序是左根右

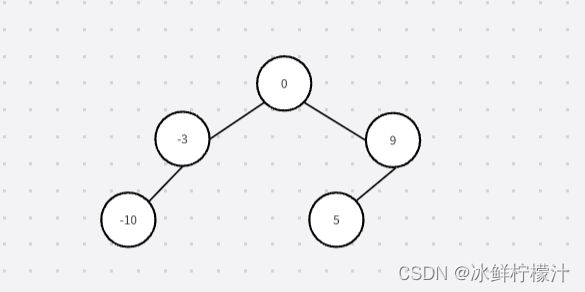
举例nums[-10,-3,0,5,9]

nums	-10	-3	0	5	9
index	0	1	2	3	4

选择中间位置左边的数字作为根节点(0+4)/2=2 j即0作为根节点root

0的左孩子是root.left=balance(nums,0,1)即-3，

balance(nums,0,0)即-10，balance(nums,0,-1)即null

0的右孩子是root.right=balance(nums,3,4)即5，

balance(nums,4,4)即9，balance(nums,5,4)即null

题目答案这张图也是符合正确的（但是我没想明白，感谢指正）

 

代码展示： 

class Solution {
    public TreeNode balance(int[] nums, int left, int right) {
        //如果左边值大于右边值返回null
        if (left > right) {
            return null;
        }
        //如果数组元素是奇数，根节点的选择是唯一的
        //如果数组元素是偶数，选择中间位置左边的数字作为根节点
        int mid = (left + right) / 2;
        //如果数组元素是偶数 选择中间位置右边的数字作为根节点
        // int mid = (left + right + 1) / 2;
        TreeNode root = new TreeNode(nums[mid]);//根节点出现

        root.left = balance(nums, left, mid - 1);//获取根节点左孩子
        root.right = balance(nums, mid + 1, right);//获取根节点右孩子
        return root;
    }
    public TreeNode sortedArrayToBST(int[] nums) {
        //这里先初始数组，获取数组元素的第一个索引和最后一个元素的索引
        return balance(nums,0,nums.length-1);
    }
}

结束拜拜！