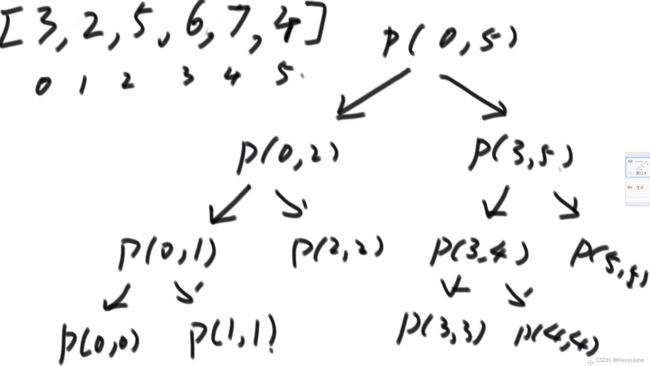认识时间复杂度和简单排序算法

目录

1 认识时间复杂度

1.1 常数时间的操作

1.2 异或运算的性质与扩展

1.3 对数器的概念和使用

1.4 剖析递归行为和递归行为时间复杂度的估算

2 常用排序算法

2.1 选择排序

2.2 冒泡排序

2.3 插入排序

---

1 认识时间复杂度

1.1 常数时间的操作

一个操作如果和样本的数据量没有关系，每次都是固定时间内完成的操作，叫做常数操作

时间复杂度为一个算法流程中，常数操作数量的一个指标。常用O（读作big O）来表示。在表达式中，只要高阶项，不要低阶项，也不要高阶项的系数，剩下的部分如果为f(N)，那么时间复杂度为O(f(N))。

评价一个算法流程的好坏，先看时间复杂度的指标，然后再分析不同数据样本下的实际运行时间，也就是“常数项时间”。

1.2 异或运算的性质与扩展

① 0^N == N N^N == 0

②异或运算满足交换律和结合律

③不用额外变量交换两个数

④一个数组中有一种数出现了奇数次，其他数出现了偶数次，怎么找到这一个数？

解决：另外取一个数，逐个和数组里的每个数进行异或运算，最后得到的值就是这个数。

⑤一个数组中有两种数出现了奇数次，其他数出现了偶数次，怎么找到这两个数？

解决：首先另外取一个数err，逐个和数组里的每个数进行异或运算，最后得到的值就是a^b，去a^b中任意一个为1的值（意味着a和b在该位不同），然后再取一个数err`，逐个和数组里的该位为1的数，得到的就是a或者b其中一个数

1.3 对数器的概念和使用

1. 有一个你想测的方法a

2. 实现复杂度不好但是容易实现的方法b

3. 实现一个随机样本产生器

4. 把方法a和方法b跑相同的随机样本，看看得到的结果是否一样

5. 如果有一个随机样本使得对比结果不一致，打印样本进行人工敢于，改对方法a或者方法b

6. 当样本数量很多时对比测试依然正确，可以确定方法a已经正确

1.4 剖析递归行为和递归行为时间复杂度的估算

用递归方法找一个数组中的最大值，系统上到底是怎么做的？

master公式的使用

T(N) = a*T(N/b) + O(N^d)

1. log(b,a) > d -> 复杂度为O(N^log(b,a))

2. log(b,a) = d -> 复杂度为O(N^d * logN)

3. log (b,a) < d -> 复杂度为O(N^d)

N为母问题中的数据，b为子问题中的规模，a为调用子问题中的次数，O(N^d)为除去子问题调用之后剩下的过程的时间复杂度

int getMax(int[] arr)
{
return process(arr , 0, arr.length - 1);
}

int process(int[] arr, int L, intR)
{
    if(L == R)
    {
        return arr[L];
    }
    int mid = L + ((R - L) >> 1) ; //中点  公式为 L + (R - L)/2 , 位运算中右移一位代表除以2
    int leftMax = process(arr, L, mid);
    int rightMax = process(arr, mid + 1, R);
    return Math.max(leftMax, rightMax);
}

 

例如求一段数组中的最大值（其中该数组中的数据量就是N），然后每次取该数组中点左右两侧（即子问题的规模为N/2，因此b为2）的最大值，每次都会调用两次（因此a为2），除去调用过程都是简单的计算，因此时间复杂度为O(1)（因此d为0）

2 常 用排序算法

2.1 选择排序

时间复杂度为O(N^2)

1. 在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，

2. 再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。

3. 以此类推，直到所有元素均排序完毕。

void SelectSort(int arr[], int len) {
	for (int i = 0; i < len; i++) {
		int mindex = i;
		for (int j = i + 1; j < len; j++) {
			if (arr[j] < arr[mindex])
				mindex = j;
		}
		int temp = arr[mindex];
		arr[mindex] = arr[i];
		arr[i] = temp;
		for (int m = 0; m < len; m++)
			cout << arr[m] << " ";
		cout << endl;
	}
}

2.2 冒泡排序

时间复杂度 O(N)

1.比较相邻的元素。如果第一个数比第二个数大，就交换他们两个。

2.对每一对相邻元素做同样的工作，从开始第一对到结尾的最后一对。在这一点，最后的元素应该会是最大的数。

3.针对所有的元素重复以上的步骤，除了最后一个。（因为最后一个已经排好，是最大的数）

4.持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。（接着排第二大的数，一直下去

#include 
using namespace std;
 
const int maxSize = 20;
 
// 冒泡排序:从小到大排序
template 
void BubbleSort(T arr[], int n) {
  int i, j, flag;
  T temp;
  
  for(i = 0; i < n-1; i++) { // 进行n-1次
    flag = 0; // 交换标志，0表示无交换，1表示有交换
    for(j = 0; j < (n-i-1); j++) { // 数组下标最大为n-1
      if(arr[j] > arr[j+1]) { // 逆序就交换
        flag = 1; // 有交换
        temp = arr[j];
        arr[j] = arr[j+1];
        arr[j+1] = temp;
      }
    }
    if(flag == 0) // 无交换,说明已经全部排好序，提前结束
      break;
  } // for
} // BubbleSort
 
int main(int argc, const char * argv[]) {
  int i, n, arr[maxSize];
  
  cout << "请输入要排序的数的个数：";
  cin >> n;
  cout << "请输入要排序的数：";
  for(i = 0; i < n; i++)
    cin >> arr[i];
  cout << "排序前：" << endl;
  for(i = 0; i < n; i++)
    cout << arr[i] << " ";
  cout << endl;
  BubbleSort(arr, n);
  cout << "排序后：" << endl;
  for(i = 0; i < n; i++)
    cout << arr[i] << " ";
  cout << endl;
  return 0;
}

2.3 插入排序

最差时间复杂度：O(n^2)
最优时间复杂度：O(n)
平均时间复杂度：O(n^2)
稳定性：稳定

插入排序算法的一般步骤：
1.从第一个元素开始，该元素可以认为已被排序；
2.取出下一个元素，在已经排序的元素序列中从后向前扫描；
3.如果该元素（已排序）大于新元素，将该元素移到下一个位置；
4.重复步骤3，直到找到已排序的元素小于或者等于新元素的位置；
5.将新元素插入到该位置后，重复2~5

void InsertionSort(int *a, int len)
{
	for (int j=1; j=0 && a[i]>key)
		{
			a[i+1] = a[i];
			i--;
		}
		a[i+1] = key;
	}
}