02-图像的几何变换

一.简介

几何空间变换是图像处理中的最基础的算法，几何变换的原理大多都是相似，只是变换矩阵不同，因此，我们以最常用的平移和旋转为例进行学习。在深度学习领域，我们常用平移、旋转、镜像等操作进行数据增广；在传统CV领域，由于某些拍摄角度的问题，我们需要对图像进行矫正处理，而几何变换正是这个处理过程的基础，因此了解和学习几何变换也是有必要的。

几何变换主要包括图像的旋转，平移，缩放，偏移，组合变换等等，在冈萨雷斯的数字图像处理第三版的第二章就做了相关介绍，最常用的空间坐标变换之一就是仿射变换。虽然仿射变换很基础，但作用还是很大的，例如在车牌识别的预处理中，首先就需要对倾斜的车牌进行矫正，然后再进行其他处理，当然这里说的是使用传统算法。

还是老样子，我们从它的原理开始。

二.算法理论介绍

首先它的变换的形式（公式）是什么？

1.公式

与OpencV不同的是这里采取冈萨雷斯的《数字图像处理_第三版》的变换矩阵方式，关于OpenCV的策略可以看它的官方文档。根据冈萨雷斯书中的描述，仿射变换的一般形式如下：

式中的T就是变换矩阵，其中 (v,w)为原坐标，(x,y) 为变换后的坐标，不同的变换对应不同的矩阵，这里也贴出来吧，一些常见的变换矩阵及作用如下表：

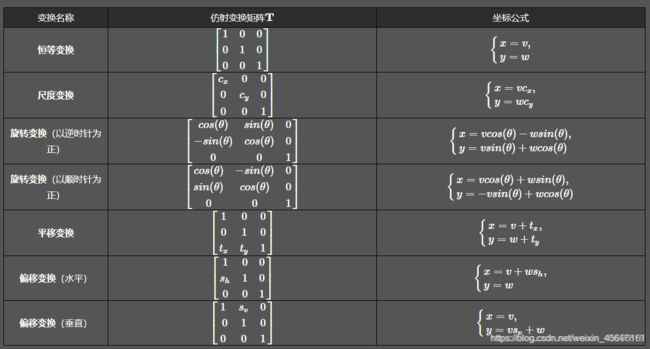
也就是说，我们根据自己的目的选择不同变换矩阵就可以了。

公式介绍了，那么接下来旋转中心是什么？毕竟以不同位置为旋转中心得到的结果是不一样的。

这个问题和坐标轴的变化有关，变换中心，对于缩放、平移可以以图像坐标原点（图像左上角为原点）为中心变换，这不用坐标系变换，直接按照一般形式计算即可。而对于旋转和偏移，一般是以图像中心为原点，那么这就涉及坐标系转换了。

2.坐标系变换

我们都知道，图像坐标的原点在图像左上角，水平向右为 X 轴，垂直向下为 Y 轴（如左图）。数学课本中常见的坐标系是以图像中心为原点，水平向右为 X 轴，垂直向上为 Y 轴，称为笛卡尔坐标系（如右图）。

因此，对于旋转和偏移，就需要3步（3次变换）：

将输入原图图像坐标转换为笛卡尔坐标系；
进行旋转计算。旋转矩阵前面已经给出了；
将旋转后的图像的笛卡尔坐标转回图像坐标。

那么现在又有一个问题，就是图像坐标系与笛卡尔坐标系应该怎么转换。想必数学好的，不用多说也知道，但是对于像我这种数学不好的同学，还是需要解释一下的。

在图像中我们的坐标系通常是AB和AC方向的,原点为A，而笛卡尔直角坐标系是DE和DF方向的，原点为D。 令图像表示为M×N的矩阵，对于点A而言，两坐标系中的坐标分别是(0，0)和(-N/2,M/2)，则图像某像素点(x’,y’)转换为笛卡尔坐标（x,y）转换关系为，x为列，y为行：

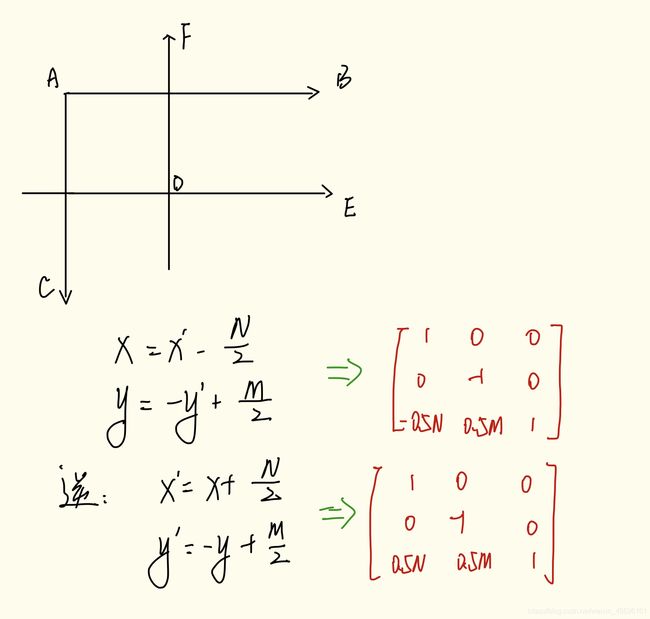
于是，根据前面说的3个步骤（3次变换），旋转(顺时针旋转)的变换形式就为，3次变换就有3个矩阵：

3.向前映射法和向后映射法

上一篇文章，我提到过向前映射法和向后映射法，在这里我再详细解释一下。
图像变换的本质是将像素点的坐标通过某一种函数关系，映射到另外的位置。

向前映射法

向前映射的过程可以分解为两步：坐标变换+分配像素值

向前映射的坐标变换：由原图像坐标推算该像素在目标图像的位置。

例如，我们知道原图像的某个像素点的坐标(x,y)，变换后在新图像的坐标为(x′,y′)，变换后的坐标一般为非整数的，而非整数的坐标是没意义的，所以将这个点的像素按权重分配给周围四个像素点。对于变换后坐标仍为整数的点，直接把其像素值分配给目标图像中对应的点即可。将原图像的所有像素点都进行这种坐标变换和分配像素值，就得到了新图像。

所以，新图像的每个像素点的像素值，都是由它周围的非整数坐标的点的像素分配给它并叠加得到的（或者直接等于某个整数坐标点的像素值）。由于这个分配、叠加的特性，向前映射法有时也叫像素移交映射。

对于向前映射，虽然原图像中的每个点分配系数之和为1。但目标图像上每个点的像素值是多个分配值叠加而成的，所以不能保证所有分配到其上的权重之和为1。因此必须记录下所有分配到其上的权重并累加起来，最后利用累加权重进行归一化，才能得到正确的插值结果。所以，确定目标图像某一点的像素值，需要遍历原图像的所有像素值，进行坐标变换和分配像素值。这是向前映射法的缺点。

向后映射法

向后映射的过程可以分解为两步：坐标变换+插值

向后映射的坐标变换：由输出图像坐标反过来推算该像素在原图像的位置。

上篇文章说的几种插值方式，就是向后映射的例子。是由目标图像的坐标算出在原图像的坐标，再确定它的像素值由原图像的哪几个点按权重分配得到。然后进行插值操作，得到该点的像素值。某一点的像素值进行一次操作就可以得到，不需要遍历全部像素点。向后映射法也叫像素填充算法。向后映射法解决了漏点的问题，出现了马赛克。

那么这里我们是用哪个效果比较好呢？

在冈萨雷斯的《数字图像处理_第三版》中说的很清楚，前向映射就是根据原图用变换公式直接算出输出图像相应像素的空间位置，那么这会导致一个问题：可能会有多个像素坐标映射到输出图像的同一位置，也可能输出图像的某些位置完全没有相应的输入图像像素与它匹配，也就是没有被映射到，造成有规律的空洞（黑色的蜂窝状）。更好的一种方式是采用 反向映射（Inverse Mapping）：扫描输出图像的位置(x,y)，通过 （为T的逆矩阵）计算输入图像对应的位置 (v,w)，通过插值方法决定输出图像该位置的灰度值。

4.插值

接下来我们要考虑哪种插值方式比较适合。

采用反向映射后，需通过插值方法决定输出图像该位置的值，因此需要选择插值算法。通常有最近邻插值、双线性插值，双三次插值等，OpencV默认采用双线性插值，我们也就采用双线性插值。

三.基于OpenCV的python实现及效果展示

在此之前我先给出OpenCV中文官方文档，大家感兴趣可以看看。

函数原型（python）：OpenCV仿射变换相关的函数一般涉及到warpAffine和getRotationMatrix2D这两个：

• OpenCV函数warpAffine 来实现一些简单的重映射；
• OpenCV函数getRotationMatrix2D 来获得旋转矩阵。

下面我用代码解释这些函数，这样印象应该会深一些。

平移

import cv2
import numpy as np

img =cv2.imread("qq.JPG")
rows = img.shape[0]       #代表行
cols = img.shape[1]       #代表列
print(rows,cols)          #个人习惯

M = np.float32([[1,0,100],[0,1,50]]) #变化矩阵 表示偏移（100，50）
dst = cv2.warpAffine(img,M,(cols,rows))
cv2.imshow('img1',img)
cv2.imshow('img2',dst)
cv2.waitKey(0)
cv2.destroyAllWindows()

cv2.warpAffine函数的第三个参数是输出图像的大小，其形式应为(width，height)。记住width =列数，height =行数。第二个参数是变换矩阵。

另外通过numpy来产生这个矩阵【要求是float类型的】，并将其赋值给函数cv2.warpAffine()。

下面是效果展示

旋转

import cv2
import numpy as np

img =cv2.imread("qq.JPG")
rows = img.shape[0]       #代表行
cols = img.shape[1]       #代表列
print(rows,cols)

M2 = cv2.getRotationMatrix2D(((cols-1)/2.0,(rows-1)/2.0),90,1) #变化矩阵 表示将图像相对于中心旋转90度而没有任何缩放比例
dst = cv2.warpAffine(img,M2,(cols,rows))
cv2.imshow('img1',img)
cv2.imshow('img2',dst)
cv2.waitKey(0)
cv2.destroyAllWindows()

在opencv中提供了cv2.getRotationMatrix2D函数获得变换矩阵。第一参数指定旋转圆点；第二个参数指定旋转角度；第三个参数指定缩放比例。

下面是效果展示

仿射变换

仿射变换是指在向量空间中进行一次线性变换(乘以一个矩阵)并加上一个平移(加上一个向量)，变换为另一个向量空间的过程。
Affine Transform描述了一种二维仿射变换的功能，它是一种二维坐标之间的线性变换，保持二维图形的“平直性”(即变换后直线还是直线，圆弧还是圆弧)和“平行性”(其实是保持二维图形间的相对位置关系不变，平行线还是平行线，而直线上的点位置顺序不变，另特别注意向量间夹角可能会发生变化)。仿射变换可以通过一系列的原子变换的复合来实现包括：平移(Translation)、缩放(Scale)、翻转(Flip)、旋转(Rotation)和错切(Shear)。

仿射变化也是需要一个M矩阵就可以，但是由于仿射变换比较复杂，很难找到这个矩阵，opencv提供了根据变换前后三个点的对应关系来自动求解M， 这个函数是cv2.getAffineTransoform(pts1, pts2)

import cv2
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt

img =cv2.imread("qq.JPG")
rows = img.shape[0]       #代表行
cols = img.shape[1]       #代表列
print(rows,cols)

pts1 = np.float32([[50,50],[200,50],[50,200]])
pts2 = np.float32([[10,100],[200,50],[100,250]])
M3 = cv2.getAffineTransform(pts1,pts2)
dst = cv2.warpAffine(img,M3,(cols,rows))

cv2.imshow('img1',img)
cv2.imshow('img2',dst)
cv2.waitKey(0)
cv2.destroyAllWindows()

在仿射变换中，原始图像中的所有平行线在输出图像中仍将平行。为了找到变换矩阵，我们需要输入图像中的三个点及其在输出图像中的对应位置。然后cv2.getAffineTransform将创建一个2x3矩阵，该矩阵将传递给cv2.warpAffine。

下面是效果展示

透视变换

首先需要了解什么是透视变换？说白了就是将2D矩阵图像变换成3D的空间显示效果，让3D空间中的2D形状的原像表现出3D的实际视觉效果。

仿射变换(affine transform)与透视变换(perspective transform)在图像还原、图像局部变化处理方面有重要意义。通常，在2D平面中，仿射变换的应用较多，而在3D平面中，透视变换又有了自己的一席之地。两种变换原理相似，结果也类似，可针对不同的场合使用适当的变换。

import cv2
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt

img =cv2.imread("qq.JPG")
rows = img.shape[0]       #代表行
cols = img.shape[1]       #代表列
print(rows,cols)

pts3 = np.float32([[56,65],[368,52],[28,387],[389,390]])
pts4 = np.float32([[0,0],[300,0],[0,300],[300,300]])
M4 = cv2.getPerspectiveTransform(pts3,pts4)
dst = cv2.warpPerspective(img,M4,(cols,rows))
cv2.imshow('img1',img)
cv2.imshow('img2',dst)
cv2.waitKey(0)
cv2.destroyAllWindows()

对于透视变换，需要3x3变换矩阵。即使在转换后，直线也将保持直线。要找到此变换矩阵，需要在输入图像上有4个点，在输出图像上需要相应的点。在这四个点中，其中三个不应共线。然后可以通过函数cv2.getPerspectiveTransform找到变换矩阵。然后将cv2.warpPerspective应用于此3x3转换矩阵。

下面是效果展示