【3维视觉】一文带你学习网格细分Mesh Subdivision算法（Loop, Butterfly, Modified Butterfly, Catmull-Clark, Doo-Sabin）

0.引言

介绍了Loop, Butterfly, Modified Butterfly, Catmull-Clark, Doo-Sabin等网格细分算法。

网格超分技术，换言之曲面细分，是指将一个模型的面合理的分成更多小的面，从而提升模型精度，提高渲染效果。经典的插值超分方法是通过一个组合更新(分裂面、添加顶点和/或插入边)和一个基于相邻顶点位置局部平均的顶点平滑来实现的。

图. 网格超分示意图

1、算法介绍

目前常见的网格主要是三角形网格（Triangle mesh）和四边形网格(Poly mesh)，网格细分算法也可以分为只能处理三角形mesh（Loop, Butterfly, Modified Butterfly）的和只能处理四边形的（Catmull-Clark），最后是能处理任意形状mesh的（ Doo-Sabin）

这些算法基本都是以Midpoint为基础，主要区别是对顶点位置的调整算法不同。

1.1 Loop细分（三角形网格）

Loop细分是Charles Loop在1987年在硕士论文Smooth subdivision surfaces based on triangles中提出的一种对三角网格的细分算法。
Loop细分是递归定义的，每一个三角形一分为四，对于新生成的顶点和旧顶点以不同的规则更新。

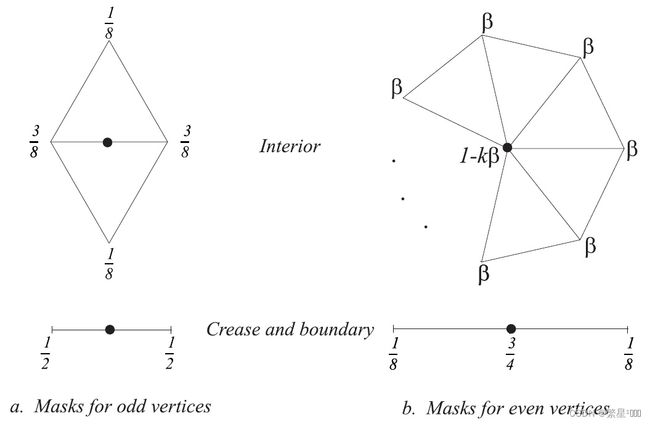
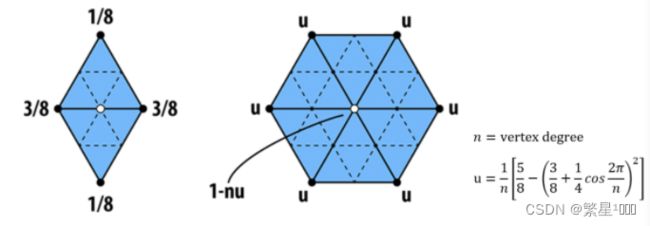
点的更新规则如下图：
左边为新生成的顶点(odd vertices)，右边为旧顶点(even vertices)
odd:偶然出现的，新顶点就是偶然出现的嘛
even: 平常的，旧顶点

更复杂的，添加了对crease处理的Loop Subdivision

crease是什么

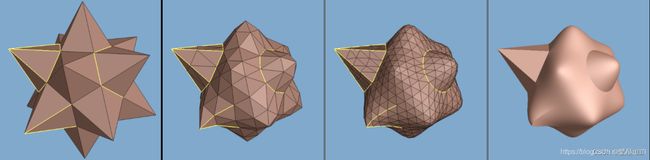
当说一条边是crease edge的时候，我们的意思其实是说这条边是sharp edge。为的是在Subdivision的时候能够保留一些锐利的部分，例如：

正常的Loop Subdivision 下图中的色边即为标记的sharp edge，标记出来的目的是为了在之后的Subdivision过程中还能保持锐利。

添加了对crease处理的Loop Subdivision Trimesh中实现的subdivide_loop代码

def subdivide_loop(vertices,
                   faces,
                   iterations=None):
    """
    Subdivide a mesh by dividing each triangle into four triangles
    and approximating their smoothed surface (loop subdivision).
    This function is an array-based implementation of loop subdivision,
    which avoids slow for loop and enables faster calculation.

    Overall process:
    1. Calculate odd vertices.
      Assign a new odd vertex on each edge and
      calculate the value for the boundary case and the interior case.
      The value is calculated as follows.
          v2
        / f0 \\        0
      v0--e--v1      /   \\
        \\f1 /     v0--e--v1
          v3
      - interior case : 3:1 ratio of mean(v0,v1) and mean(v2,v3)
      - boundary case : mean(v0,v1)
    2. Calculate even vertices.
      The new even vertices are calculated with the existing
      vertices and their adjacent vertices.
        1---2
       / \\/ \\      0---1
      0---v---3     / \\/ \\
       \\ /\\/    b0---v---b1
        k...4
      - interior case : (1-kB):B ratio of v and k adjacencies
      - boundary case : 3:1 ratio of v and mean(b0,b1)
    3. Compose new faces with new vertices.

    Parameters
    ------------
    vertices : (n, 3) float
      Vertices in space
    faces : (m, 3) int
      Indices of vertices which make up triangles

    Returns
    ------------
    vertices : (j, 3) float
      Vertices in space
    faces : (q, 3) int
      Indices of vertices
    iterations : int
          Number of iterations to run subdivision
    """
    try:
        from itertools import zip_longest
    except BaseException:
        # python2
        from itertools import izip_longest as zip_longest

    if iterations is None:
        iterations = 1

    def _subdivide(vertices, faces):
        # find the unique edges of our faces
        edges, edges_face = faces_to_edges(
            faces, return_index=True)
        edges.sort(axis=1)
        unique, inverse = grouping.unique_rows(edges)

        # set interior edges if there are two edges and boundary if there is
        # one.
        edge_inter = np.sort(
            grouping.group_rows(
                edges,
                require_count=2),
            axis=1)
        edge_bound = grouping.group_rows(edges, require_count=1)
        # make sure that one edge is shared by only one or two faces.
        if not len(edge_inter) * 2 + len(edge_bound) == len(edges):
            # we have multiple bodies it's a party!
            # edges shared by 2 faces are "connected"
            # so this connected components operation is
            # essentially identical to `face_adjacency`
            faces_group = graph.connected_components(
                edges_face[edge_inter])

            if len(faces_group) == 1:
                raise ValueError('Some edges are shared by more than 2 faces')

            # collect a subdivided copy of each body
            seq_verts = []
            seq_faces = []
            # keep track of vertex count as we go so
            # we can do a single vstack at the end
            count = 0
            # loop through original face indexes
            for f in faces_group:
                # a lot of the complexity in this operation
                # is computing vertex neighbors so we only
                # want to pass forward the referenced vertices
                # for this particular group of connected faces
                unique, inverse = grouping.unique_bincount(
                    faces[f].reshape(-1), return_inverse=True)

                # subdivide this subset of faces
                cur_verts, cur_faces = _subdivide(
                    vertices=vertices[unique],
                    faces=inverse.reshape((-1, 3)))

                # increment the face references to match
                # the vertices when we stack them later
                cur_faces += count
                # increment the total vertex count
                count += len(cur_verts)
                # append to the sequence
                seq_verts.append(cur_verts)
                seq_faces.append(cur_faces)

            # return results as clean (n, 3) arrays
            return np.vstack(seq_verts), np.vstack(seq_faces)

        # set interior, boundary mask for unique edges
        edge_bound_mask = np.zeros(len(edges), dtype=bool)
        edge_bound_mask[edge_bound] = True
        edge_bound_mask = edge_bound_mask[unique]
        edge_inter_mask = ~edge_bound_mask

        # find the opposite face for each edge
        edge_pair = np.zeros(len(edges)).astype(int)
        edge_pair[edge_inter[:, 0]] = edge_inter[:, 1]
        edge_pair[edge_inter[:, 1]] = edge_inter[:, 0]
        opposite_face1 = edges_face[unique]
        opposite_face2 = edges_face[edge_pair[unique]]

        # set odd vertices to the middle of each edge (default as boundary
        # case).
        odd = vertices[edges[unique]].mean(axis=1)
        # modify the odd vertices for the interior case
        e = edges[unique[edge_inter_mask]]
        e_v0 = vertices[e][:, 0]
        e_v1 = vertices[e][:, 1]
        e_f0 = faces[opposite_face1[edge_inter_mask]]
        e_f1 = faces[opposite_face2[edge_inter_mask]]
        e_v2_idx = e_f0[~(e_f0[:, :, None] == e[:, None, :]).any(-1)]
        e_v3_idx = e_f1[~(e_f1[:, :, None] == e[:, None, :]).any(-1)]
        e_v2 = vertices[e_v2_idx]
        e_v3 = vertices[e_v3_idx]

        # simplified from:
        # # 3 / 8 * (e_v0 + e_v1) + 1 / 8 * (e_v2 + e_v3)
        odd[edge_inter_mask] = 0.375 * e_v0 + \
            0.375 * e_v1 + e_v2 / 8.0 + e_v3 / 8.0

        # find vertex neighbors of each vertex
        neighbors = graph.neighbors(
            edges=edges[unique],
            max_index=len(vertices))
        # convert list type of array into a fixed-shaped numpy array (set -1 to
        # empties)
        neighbors = np.array(list(zip_longest(*neighbors, fillvalue=-1))).T
        # if the neighbor has -1 index, its point is (0, 0, 0), so that
        # it is not included in the summation of neighbors when calculating the
        # even
        vertices_ = np.vstack([vertices, [0.0, 0.0, 0.0]])
        # number of neighbors
        k = (neighbors + 1).astype(bool).sum(axis=1)

        # calculate even vertices for the interior case
        even = np.zeros_like(vertices)

        # beta = 1 / k * (5 / 8 - (3 / 8 + 1 / 4 * np.cos(2 * np.pi / k)) ** 2)
        # simplified with sympy.parse_expr('...').simplify()
        beta = (40.0 - (2.0 * np.cos(2 * np.pi / k) + 3)**2) / (64 * k)
        even = beta[:, None] * vertices_[neighbors].sum(1) \
            + (1 - k[:, None] * beta[:, None]) * vertices

        # calculate even vertices for the boundary case
        if edge_bound_mask.any():
            # boundary vertices from boundary edges
            vrt_bound_mask = np.zeros(len(vertices), dtype=bool)
            vrt_bound_mask[np.unique(edges[unique][~edge_inter_mask])] = True
            # one boundary vertex has two neighbor boundary vertices (set
            # others as -1)
            boundary_neighbors = neighbors[vrt_bound_mask]
            boundary_neighbors[~vrt_bound_mask[neighbors[vrt_bound_mask]]] = -1

            even[vrt_bound_mask] = (vertices_[boundary_neighbors].sum(axis=1) / 8.0 +
                                    (3.0 / 4.0) * vertices[vrt_bound_mask])

        # the new faces with odd vertices
        odd_idx = inverse.reshape((-1, 3)) + len(vertices)
        new_faces = np.column_stack([
            faces[:, 0],
            odd_idx[:, 0],
            odd_idx[:, 2],
            odd_idx[:, 0],
            faces[:, 1],
            odd_idx[:, 1],
            odd_idx[:, 2],
            odd_idx[:, 1],
            faces[:, 2],
            odd_idx[:, 0],
            odd_idx[:, 1],
            odd_idx[:, 2]]).reshape((-1, 3))

        # stack the new even vertices and odd vertices
        new_vertices = np.vstack((even, odd))

        return new_vertices, new_faces

    for _ in range(iterations):
        vertices, faces = _subdivide(vertices, faces)

    if tol.strict or True:
        assert np.isfinite(vertices).all()
        assert np.isfinite(faces).all()
        # should raise if faces are malformed
        assert np.isfinite(vertices[faces]).all()

        # none of the faces returned should be degenerate
        # i.e. every face should have 3 unique vertices
        assert (faces[:, 1:] != faces[:, :1]).all()

    return vertices, faces

1.2 Butterfly

蝴蝶算法是一种常用的插值细分算法，由NIRA DYN and DAVID LEVIN (Tel-Aviv University) and JOHN A. GREGORY (Brunei University)在论文A Butterfly Subdivision Scheme for Surface Interpolation with Tension Control 提出。

Butterfly 只对新插入的点处理，对新插入的顶点分了两种情况：

1. 内部点：位于内部边的点
   - 内部边的两个端点度都为6时
   - 内部边的一个端点度为6时
   - 内部边的两个端点度都不为6时
2. 边界点：位于边界边的点
   
   注意，Butterfly模板假设有一个规则的邻域，即，要处理的边[a, b]的顶点a和b都恰好有6个邻域。此外，Butterfly要求表面是局部流形，即模板中的每条边至少有一个面连接到它(边界边)，最多有两个面(内部边)。

1.3 Modified butterfly

Denis Zoriny, Peter Schr ¨odery, Wim Sweldens在论文Interpolating Subdivision for Meshes with Arbitrary Topology中提出了改进的蝴蝶算法，可以在任意的三角网格上生成G1连续的细分曲面。对Butterfly方案的主要修改在于处理价不等于6的点，它克服了butterfly方案在这些情况下表现出的尖点状伪影。

新插入的点（即所谓奇点）都在已有三角形的边上。对于它们的坐标点的计算，将分以下几种情况：

3.1奇点所在边的两个端点的度均为6

如上图所示，中间黄色点为插入的奇点，它的坐标值通过周围八个点（绿色）的坐标值加权平均得到。并且周围的点按权重不同可分为三类，各自权重如下：a = 1/2，b = 1/8，c = -1/16

3.2 奇点所在边的两个端点中一个端点的度为6，另一个不为6

如图4所示，奇点所在的边的两个端点中，点v的度不为6，点e0的度为6，则奇点的坐标值要根据点v及v的所有相邻点（绿色）的坐标加权得到。

• v点的权重：v = 3/4
• 剩下1/4的权重根据v点周围点的数量分配给周围点（e0也是v的周围点）

假设点v共有n个邻点，则各邻结点的权值可根据n值的不同分别计算：

n = 3时：e0 = 5/12，e1 = e2 = -1/12；

n = 4时：e0 = 3/8，e1 = 0，e2 = -1/8，e3 = 0；

n ≥ 5时：$e_j=(1/4+cos(2\pi \ast j/n)+1/2\ast cos(4\pi \ast j/n))/n$，其中$j=0，1，\dots ，n-1$。

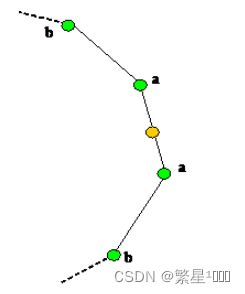
注意特殊情况：如果处理的模型是非闭合的，即处理的模型有开口。那么当寻找v周围的顶点并保存时，应该注意存储顶点的顺序问题，如下图所示情况：

当前处理的边是(v1,v2)，假设一向上找周围顶点，找到边(v1,3)遇到边界边停止，想要找剩下的顶点就需要从(v1,v2)向下寻找，找到点的顺序是5,4.在最终存储时需要将向下寻找时找到的点倒序存到123后面才能保证顺序正确。

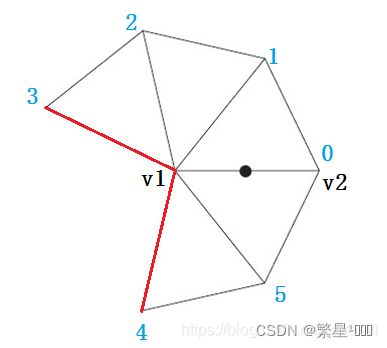
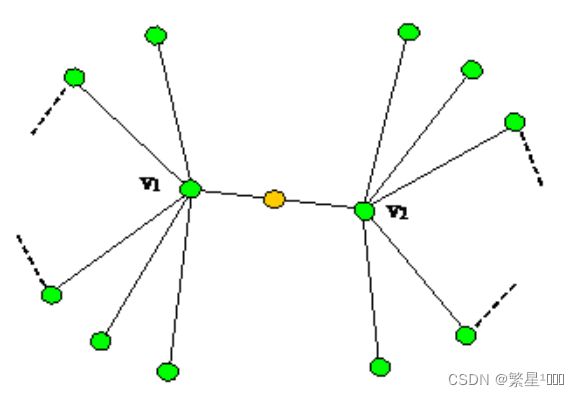
3.3 当奇点所在边的两个端点的度均不为6时（如图5）

先以v1为中心，按前述（3.2）情况中的方法计算出奇点的坐标，记为(x1，y1，z1)，再以v2为中心同样计算出奇点的坐标，记为(x2，y2，z2)，然后对两组坐标取平均值，得到奇点的坐标。

3.4 奇点所在边是边界时采用四点法。

当网格不闭合时存在这种情况，此时参与计算的各点的权值取值如下：

a = 9/16，b = -1/16

1.4 Catmull-Clark细分（四边形网格）

Catmull-Clark细分是Edwin CatMull和Jin Clark在1978年提出的一种可以对任意拓扑的网格进行细分的一种算法，是递归定义的，在每一次递归中：
分如下5种情况处理点：

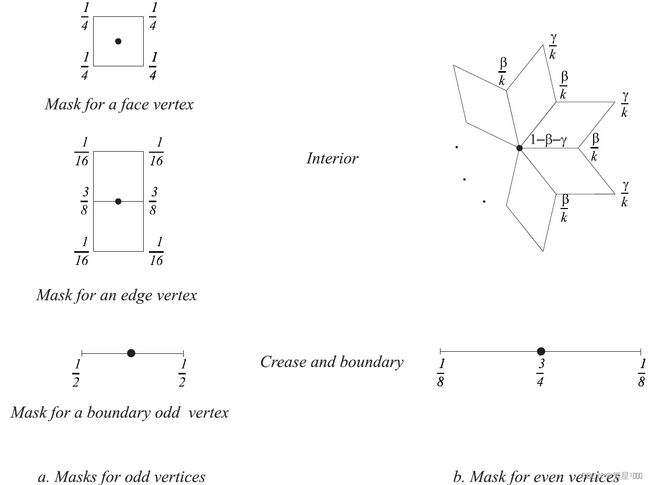
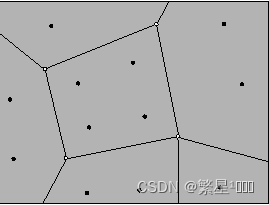
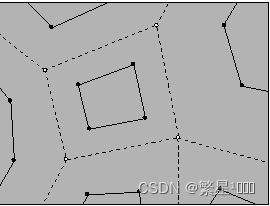
1.5 Doo-Sabin细分

Doo-Sabin细分是Dainel Doo和Malcolm Sabin在1978年在论文Behaviour of recursive division surfaces near extraordinary points提出的一种可以对任意拓扑的网格进行细分的一种算法，是递归定义的。
原来的顶点变面（度为几，就是几边形）
边也变面
原来的面也变为新面

在每一次递归中：

• 计算面的中心点和边的中心点，对于每一个点P，计算一个新的点P’, 是原顶点，相邻的边的中心点和面的中心点的平均值。
  

• 对于每一个面，连接面内的新点生成新的面

  

• 对于每一个点，连接点周围的新点生成新的面
  

• 对于每一条边，连接边相邻的新点生成新的面

2、对比

Loop只能用于三角形网格，Catmull-Clark可以运用于任意拓扑的网格

Doo-Sabin的计算效率不如Catmull-Clark

在3D计算机图形学中，Doo-Sabin细分曲面是一种基于双二次均匀B样条推广的细分曲面，而Catmull-Clark基于广义双立方均匀B样条。

评估
Doo-Sabin曲面以递归方式定义。与所有细分过程一样，每次细化迭代都按照给定的过程，将当前网格替换为“更平滑”、更精细的网格。经过多次迭代后，曲面将逐渐收敛到光滑的极限曲面上。

就像Catmull-Clark曲面一样，Doo-Sabin极限曲面也可以通过Jos Stam的技术直接评估，而无需任何递归细化。然而，该解决方案的计算效率不如 Catmull-Clark 曲面，因为 Doo-Sabin 细分矩阵（通常）不可对角化。

3、参考资料

[1] Mesh-Subdivision(Github)

[2] loop曲面细分算法c++实现

[3] Doo-sabin曲面

[4] 细分曲面Catmull-Clark Subdivision算法

[5]【图形学实验】Loop Subdivision与Modified Butterfly Subdivision

[6] 改进的蝴蝶算法详细介绍

[7] 三维网格细分算法（Catmull-Clark subdivision & Loop subdivision）附源码