R语言：Plot3D包绘制等高线图及分层设色地形图

一.色彩矩阵绘制

通过颜色深浅程度 矩阵面积大小来反映数值的数据规律，如下例：

随机生成的矩阵数据为：

> View(zrc)
> zrc
          [,1]      [,2]      [,3]
[1,] 0.5935122 0.3274156 0.1338633
[2,] 0.1476645 0.6753859 0.7945451
[3,] 0.5833544 0.5239057 0.8229289

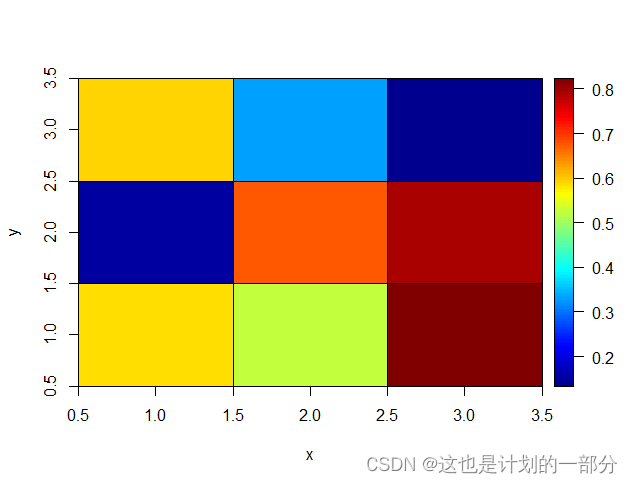
绘制色彩矩阵如下：

能够快速依据颜色的变化来判断矩阵数值的分布

R语言代码：

x <- 1:3
y = 1:3
u<-runif(length(x)*length(y))
z = matrix (nrow = 3, ncol = 3, data = u)
zt = t(z)
zrc <- apply(zt, 2, rev)
image2D(z,x,y,border = "black")

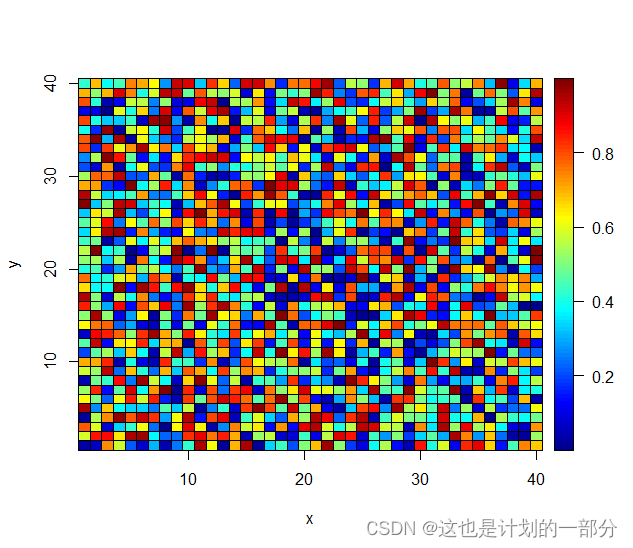
当然也可以调整为更高的维度 并无太大的意义：

上述色彩矩阵的用处并不是很大 直观地观察数据一样能够看出数据的大小等关系。

但倘若数据规模足够大 而且存在一定规律，我们能够获得良好的效果，接下来我们进行举例。

二.地形数据集

volcano: 沃特卡诺莫恩加沃(伊登山)是奥克兰火山区内约50座火山之一。该数据集在10米乘10米的网格上提供了相应的地形信息。

data(volcano)

三.分层设色地形图

按照越高越亮或者越高越暗的原则，在不同的等高线之间，着上不同的颜色，可以一目了然的看出地面的高低形态和海底的起伏状况。

我们假设一个情景 一座孤立的海岛 四周都是海洋而中间是小山丘 如何用二维图形表示？

利用上述色彩矩阵，我们能够获得很好的运用效果，如图所示：

一个很明显的数据分布规律 数据向中间以环形的形式递增。

四.地形图扩展

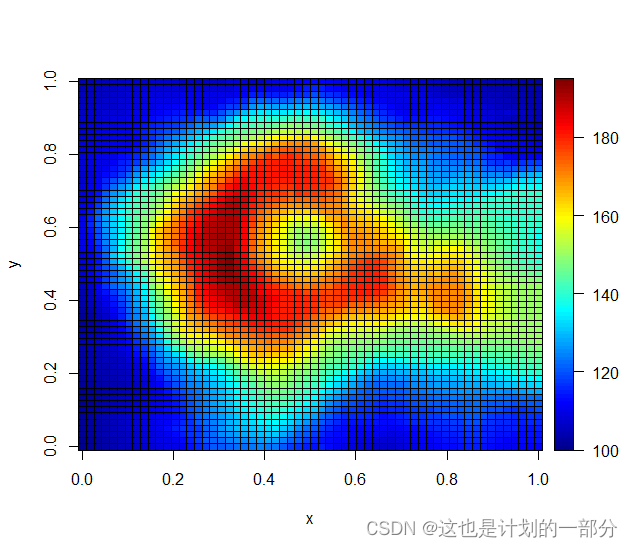
能够展示更加立体一些的效果，照亮突出地势的变化，或是添加网格/绘制等高线等等。

效果如图所示：

代码:

par(mfrow = c(2, 2))
nr <- nrow(volcano)
nc <- ncol(volcano)
image2D(volcano, x = 1:nr, y = 1:nc, lighting = TRUE,
        main = "volcano", clab = "height, m")
image2D(z = volcano, x = 1:nr, y = 1:nc, lwd = 2, shade = 0.2,
        main = "volcano", clab = "height, m")
image2D(volcano, x = 1:nr, y = 1:nc, contour = TRUE, shade = 0.5, lphi = 0,
        col = "lightblue", main = "volcano")
breaks <- seq(90, 200, by = 10)
image2D(volcano, x = 1:nr, y = 1:nc, col = jet.col(length(breaks)-1),
        main = "volcano", clab = "height, m", breaks = breaks)

abline(v = seq(10, 80, by = 10))
abline(h = seq(10, 60, by = 10))