NUAA模式识别实验报告

模式识别实验报告

题目一

​实现至少一个无监督算法：K-均值、ISOData算法、GMM算法等等。并通过数据集实验讨论其性能。可直接使用他人开源代码。任意自选数据集。

K-均值算法

1.算法原理

概念

​ K-均值（K-Means）算法是典型的基于距离的聚类算法，采用距离作为相似性的评价指标，即认为两个对象的距离越近，其相似度就越大。该算法认为簇是由距离靠近的对象组成的，因此把得到紧凑且独立的簇作为最终目标。
​ K个初始聚类中心点的选取对聚类结果具有较大的影响，因为在该算法第一步中是随机地选取任意k个对象作为初始聚类中心，初始地代表一个簇。该算法在每次迭代中对数据集中剩余的每个对象，根据其与各个簇中心的距离赋给最近的簇。当考查完所有数据对象后，一次迭代运算完成，新的聚类中心被计算出来。

算法思想

​ 时间复杂度
$$O(tknm)$$
​ 其中，t 为迭代次数，k 为簇的数目，n 为样本点数，m 为样本点维度。

​ 空间复杂度
$$O(m(n+k))$$
​ 其中，k 为簇的数目，m 为样本点维度，n 为样本点数。

2.实验内容

​ 了解K-均值算法，加强对非监督学习算法的理解和认识。采用开源代码，了解其算法思想，通过控制变量法探讨迭代次数n和分类数K的取值对实验结果的影响。找到分类结果收敛的最小n值和最合适的分类数目K值。

3.实验环境

• Windows10操作系统
• Python 3.8
• PyCharm工作台

4.实验代码

import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
mpl.rcParams['font.sans-serif'] = ['KaiTi', 'SimHei', 'FangSong']  # 汉字字体,优先使用楷体，如果找不到楷体，则使用黑体
mpl.rcParams['font.size'] = 12  # 字体大小
mpl.rcParams['axes.unicode_minus'] = False  # 正常显示负号

# from numpy.random import ranf
# Fixing random state for reproducibility

np.random.seed(2019071)

def centerPoint(group):
    n = group.shape[0]
    if n != 0:
        sum_ = np.sum(group, axis=0)
        return sum_ / n
    else:
        return None

def generateData(N=5000):
    N1 = int(np.random.randint(N, size=1, ))
    mu, sigma = 1.5, 0.2
    x1 = mu + sigma * np.random.randn(N1)
    mu, sigma = 1.6, 0.08
    y1 = mu + sigma * np.random.randn(N1)
    N2 = N - N1
    mu, sigma = 1.3, 0.15
    x2 = mu + sigma * np.random.randn(N2)
    mu, sigma = 2.3, 0.14
    y2 = mu + sigma * np.random.randn(N2)
    data = np.concatenate((list(zip(x1, y1)), list(zip(x2, y2))), axis=0)
    return data

def classfy(data, seeds):
    K = len(seeds)
    groups = [[] for i in range(K)]
    N = len(data)
    for i in range(N):
        point = data[i]

        distance_min = np.linalg.norm(point - seeds[0])
        index_min = 0
        for j in range(1, K):
            distance = np.linalg.norm(point - seeds[j])
            if distance < distance_min:
                distance_min = distance
                index_min = j

        groups[index_min].append(point)
    for j in range(0, K):
        groups[j] = np.array(groups[j])
    return groups

def distanceSum(groups, seeds):
    s = 0
    for i in range(len(groups)):
        if groups[i].shape[0] == 0 or seeds[i] is None:
            continue
        s += np.sum(np.linalg.norm(groups[i] - seeds[i]))
    return s

data = generateData(N=5000)
print("data.shape: ", data.shape)
print(data)
# seeds表示分类数
seed0 = [1.8, 2.8]  #
seed1 = [1.5, 1.5]
seed2 = [1.2, 2.0]
seeds = [seed0, seed1, seed2]
# seeds = [seed0,seed1]
distanceSum_log = []  # 用于查看收敛与否
colors = ['g', 'b', 'orange', 'cyan', 'yellow', 'magenta']
# n 次迭代，更改n即更改迭代次数
n = 5
for i in range(n):
    # center point
    for j in range(len(seeds)):
        if seeds[j] is not None:
            plt.scatter(seeds[j][0], seeds[j][1], s=35, c="red", alpha=1, zorder=2)

    groups = classfy(data, seeds)  # 分类

    distanceSum_log.append(distanceSum(groups, seeds))
    for j in range(len(seeds)):
        seeds[j] = centerPoint(groups[j])
        if groups[j].shape[0] == 0:
            continue
        # plt.scatter(groups[j][:,0],groups[j][:,1],s=5,c=(ranf(),ranf(),ranf()),alpha=1)
        plt.scatter(groups[j][:, 0], groups[j][:, 1], s=5, c=colors[j], alpha=1)

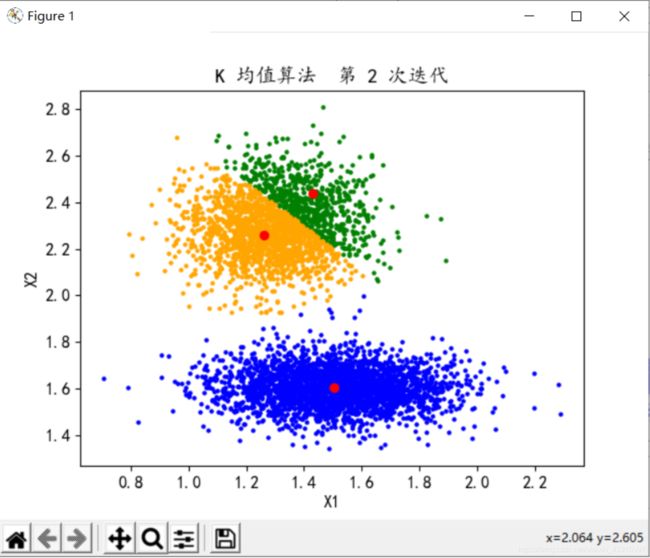
    plt.title("K 均值算法  第 %d 次迭代" % i)
    plt.xlabel("X1")
    plt.ylabel("X2")
    plt.show()
plt.plot(range(1, n + 1), distanceSum_log)
plt.scatter(range(1, n + 1), distanceSum_log)
plt.title("到各中心点距离之和")
plt.xlabel("迭代次数")
plt.show()

5.实验结果

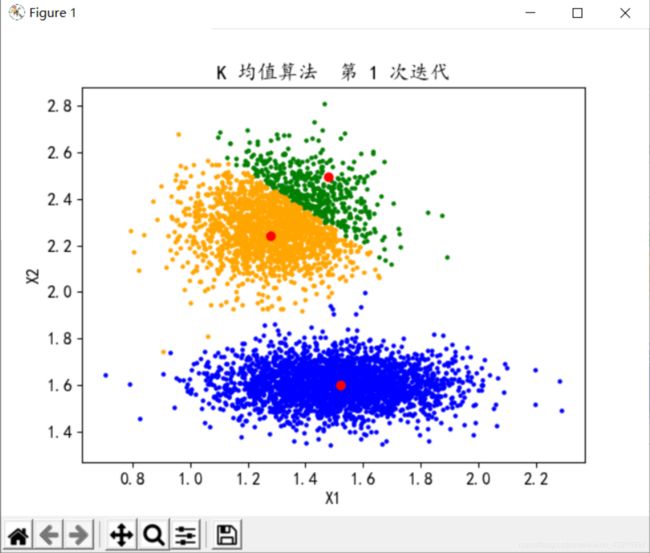
• 迭代次数n的讨论

  分类数K=3，迭代次数n=2

​ 分类数K=3，迭代次数n=3

​ 分类数K=3，迭代次数n=5

• 分类数K的讨论

  ​ 迭代次数n=3，分类数K=2

  

  ​ 迭代次数n=3，分类数K=3

6.分析讨论

​ 1、分析可知，迭代次数当增大到一定值后，聚类中心不发生变化，分类结果已经收敛，很多时候我们可能不必跑到最终结果，因此可以选择此时的n为迭代次数，大概就是折线图的折点，多于n消耗更多的性能，小于n结果可能并未达到理想条件。本案例中在n等于3-5时，聚类中心基本不再改变，因此可取n为3-5。算法逻辑简单，处理数据时具有可伸缩性和高效性。

​ 2、对应本例的数据集，通过对比分类数K的值，可以得出结论：当分类数K=2时，类之间的区别更加明显，此时分类效果最好。所以说，分类数K值的选取需要一定的考虑。在大多数情况下，K值是未预先定义的，因此许多场景下K-均值算法并没有办法进行下去。但是，也有一些改进方法，对于可以确定K值不会太大但不明确精确的K值的场景，可以进行迭代运算，然后找出Cost Function最小时所对应的K值，这个值往往能较好的描述有多少个簇类。

7.个人感想

​ K-均值算法让我对无监督算法有了一定的了解。无监督的训练样本没有标签信息。K-均值算法原理和实现还是相对简单的，调参也方便些，并且可解释度强。在一些情况下，达到最优分类效果，则需要跑到分类结果完全收敛，此时调节类别K即可。当类别K确定时，调节迭代次数n可找到最优的折点。但是同样存在着缺点，K值不好选取，手动调节也无法证明哪个K是最优的。采用迭代也只是局部最优。对于噪音和异常点比较敏感。

​ 我对算法的学习了解只是九牛一毛，未来学习的路还有很长，还是需要一步一个脚印的走下去！

题目二

​ 阅读经典论文，对任意两种有监督分类算法（感知器、SVM、Adaboost、随机森林等等）进行量化实验分析和对比，可直接使用他人开源代码，重在实验过程和结果量化分析。任意自选数据集。

Lfw Face Recognition

1.概念先知

人脸识别

​ 人脸识别是基于人的脸部特征信息进行身份识别的一种生物识别技术。用摄像机或摄像头采集含有人脸的图像或视频流，并自动在图像中检测和跟踪人脸，进而对检测到的人脸进行脸部识别的一系列相关技术，通常也叫做人像识别、面部识别。

SVM支持向量机

​ 支持向量机（support vector machines, SVM）是一种二分类模型，它的基本模型是定义在特征空间上的间隔最大的线性分类器，间隔最大使它有别于感知机；SVM还包括核技巧，这使它成为实质上的非线性分类器。SVM的的学习策略就是间隔最大化，可形式化为一个求解凸二次规划的问题，也等价于正则化的合页损失函数的最小化问题。SVM的的学习算法就是求解凸二次规划的最优化算法。

​ 核心思想

• 它是针对线性可分情况进行分析，对于线性不可分的情况，通过使用非线性映射算法将低维输入空间线性不可分的样本转化为高维特征空间使其线性可分，从而使得高维特征空间采用线性算法对样本的非线性特征进行线性分析成为可能。
• 它基于结构风险最小化理论之上再特征空间中构建最优超平面，使得学习器得到全局最优化，并且在整个样本空间的期望以某个概率满足一定上界。

Adaboost自适应提升算法

​ Adaboost是一种迭代算法，其核心思想是针对同一个训练集训练不同的分类器(弱分类器)，然后把这些弱分类器集合起来，构成一个更强的最终分类器（强分类器）。对AdaBoost算法的研究以及应用大多集中于分类问题，同时也出现了一些在回归问题上的应用。就其应用AdaBoost系列主要解决了: 两类问题、多类单标签问题、多类多标签问题、大类单标签问题、回归问题。它用全部的训练样本进行学习。

​ 核心思想

• 初始化所有样本的权重，让所有样本的权重的初始值相等。
• 用样本的一个子集来创建一个弱分类器（比如一棵决策树）。
• 用刚创建的弱分类器，对所有的样本进行预测，获得预测结果。
• 增大预测错误的样本的权重。
• 在更新了权重的样本上创建第二个弱分类器。
• 依此类推，继续创建若干个弱分类器，直至新创建的弱分类器的精度不再变化，或者达到了弱分类器数目的上限。
• 把上面生成的弱分类器组合成一个强分类器。

Random Forest随机森林

​ 随机森林就是通过集成学习的思想将多棵树集成的一种算法，它的基本单元是决策树，随机森林是由很多决策树构成的，不同决策树之间没有关联。它的本质属于机器学习的一大分支——集成学习（Ensemble Learning）方法。

​ 核心思想

• 用N来表示训练用例（样本）的个数，M表示特征数目。
• 输入特征数目m，用于确定决策树上一个节点的决策结果；其中m应远小于M。
• 从N个训练用例（样本）中以有放回抽样的方式，取样N次，形成一个训练集（即bootstrap取样），并用未抽到的用例（样本）作预测，评估其误差。
• 对于每一个节点，随机选择m个特征，决策树上每个节点的决定都是基于这些特征确定的。根据这m个特征，计算其最佳的分裂方式。
• 每棵树都会完整成长而不会剪枝，这有可能在建完一棵正常树状分类器后会被采用）。

2.实验内容

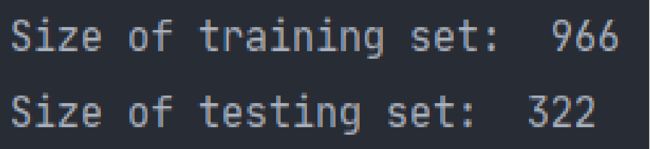
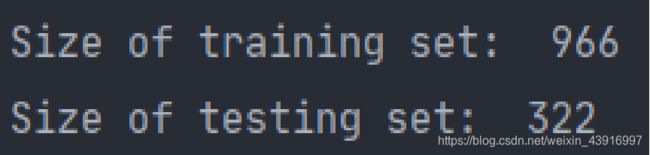
​ 采用PCA特征提取，SVM和Adaboost、Random Forest等方法进行LFW *(Labled Faces in the Wild)*数据集人脸分类识别实验。进行量化实验后，通过准确率以及混淆矩阵等指标进行模型的评价。

3.实验环境

• Windows10操作系统
• Python 3.8
• PyCharm工作台

4.关键代码

人脸数据集的特征脸算法&无监督特征提取&降维

n_components = 150
print("Extracting the top %d eigenfaces from %d faces"
      % (n_components, X_train.shape[0]))
t0 = time()
pca = PCA(n_components=n_components, svd_solver='randomized',
          whiten=True).fit(X_train)
print("done in %0.3fs" % (time() - t0))

eigenfaces = pca.components_.reshape((n_components, h, w))

print("Projecting the input data on the eigenfaces orthonormal basis")
t0 = time()
X_train_pca = pca.transform(X_train)
X_test_pca = pca.transform(X_test)
print("done in %0.3fs" % (time() - t0))

print("shape of xtrain_pca")
print(X_train_pca.shape)

训练SVM分类模型部分

print("Fitting the classifier to the training set")
t0 = time()
param_grid = {'C': [1e3, 5e3, 1e4, 5e4, 1e5],
              'gamma': [0.0001, 0.0005, 0.001, 0.005, 0.01, 0.1], }
clf = GridSearchCV(SVC(kernel='rbf', class_weight='balanced'), param_grid)
clf = clf.fit(X_train_pca, y_train)
#X_train_pca
print("done in %0.3fs" % (time() - t0))
print("Best estimator found by grid search:")
print(clf.best_estimator_)

训练Adaboost分类模型部分

bdt_real = AdaBoostClassifier(
    DecisionTreeClassifier(max_depth=4),
    n_estimators=300,
    learning_rate=0.8)

bdt_discrete = AdaBoostClassifier(
    DecisionTreeClassifier(max_depth=4),
    n_estimators=300,
    learning_rate=0.8,
    algorithm="SAMME")

bdt_discrete.fit(X_train_pca, y_train)
discrete_test_errors = []

for discrete_train_predict in zip(
        bdt_discrete.staged_predict(X_test_pca)):
    discrete_test_errors.append(
        1. - accuracy_score(discrete_train_predict, y_test))

训练Random Forest分类模型部分

randomforest_clf = RandomForestClassifier(n_estimators= 80 ,max_depth = 10)
randomforest_clf=randomforest_clf.fit(X_train_pca, y_train)
y_randomforest_pred = randomforest_clf.predict(X_test_pca)

5.实验结果

SVM

一些特征脸以及部分预测结果图

预测结果

	precision	recall	f1-score	support
Colin Powell	0.94	0.94	0.94	64
Donald Rumsfeld	0.96	0.84	0.90	32
George W Bush	0.88	0.97	0.92	127
Gerhard Schroeder	1.00	0.86	0.93	29
Tony Blair	0.93	0.82	0.87	33
accuracy			0.92	285
macro avg	0.94	0.89	0.91	285
weighted avg	0.92	0.92	0.92	285

混淆矩阵
$$\begin{array}{ccccc}60& 0& 4& 0& 0\\ 0& 27& 4& 0& 1\\ 4& 0& 123& 0& 0\\ 0& 0& 3& 25& 1\\ 0& 1& 5& 0& 27\end{array}$$

Adaboost

一些特征脸以及部分预测结果图

预测结果

	precision	recall	f1-score	support
Ariel Sharon	1.00	0.15	0.27	13
Colin Powell	0.81	0.72	0.76	60
Donald Rumsfeld	0.62	0.37	0.47	27
George W Bush	0.68	0.94	0.79	146
Gerhard Schroeder	0.79	0.44	0.56	25
Hugo Chavez	0.67	0.13	0.22	15
Tony Blair	0.61	0.56	0.58	36
accuracy			0.70	322
macro avg	0.74	0.47	0.52	322
weighted avg	0.71	0.70	0.67	322

混淆矩阵
$$\begin{array}{ccccccc}2& 2& 3& 6& 0& 0& 0\\ 0& 43& 0& 15& 0& 0& 2\\ 0& 1& 10& 14& 1& 0& 1\\ 0& 2& 3& 137& 1& 0& 3\\ 0& 2& 0& 7& 11& 1& 4\\ 0& 1& 0& 8& 1& 2& 3\\ 0& 2& 0& 14& 0& 0& 20\end{array}$$

Random Forest

	precision	recall	f1-score	support
Ariel Sharon	0.00	0.00	0.00	13
Colin Powell	0.84	0.60	0.70	60
Donald Rumsfeld	0.75	0.11	0.19	27
George W Bush	0.57	0.99	0.72	146
Gerhard Schroeder	0.67	0.24	0.35	25
Hugo Chavez	1.00	0.07	0.12	15
Tony Blair	0.50	0.17	0.25	36
accuracy			0.61	322
macro avg	0.62	0.31	0.33	322
weighted avg	0.63	0.61	0.53	322

混淆矩阵
$$\begin{array}{ccccccc}0& 1& 1& 10& 0& 0& 1\\ 0& 36& 0& 22& 1& 0& 1\\ 0& 1& 3& 23& 0& 0& 0\\ 0& 0& 0& 144& 1& 0& 1\\ 0& 2& 0& 15& 6& 0& 2\\ 0& 2& 0& 11& 0& 1& 1\\ 0& 1& 0& 28& 1& 0& 6\end{array}$$

6.分析讨论

​ 1.根据预测矩阵求得，5类人脸预测的准确率，SVM>RandomForest>Adaboost。Adaboost识别率比不上SVM可能是由于Adaboost需求的数据集更大。两者各有缺陷，因此可以提出一种基于Adaboost的SVM分类器，这样我相信性能会大大提升。

​ 2.对于Adaboost和RandomForest，采用了同样的数据集与测试集，我们可以发现训练集很少时，Random Forest算法可能存在预测的准确率为0，而Adaboost不存在。但是随着训练集增加，Random Forest预测的准确率也会增加。SVM分类器与训练集的拟合时间更长，并且不易过拟合。

7.个人感想

​ 通过学习SVM，Random Forest，Adaboost三个算法，简单的了解了有监督学习算法。有监督学习将包含特征和标签信息的样本作为训练样本，通过训练样本训练得到一个最优模型，再利用这个模型将所有的输入映射为相应的输出，对输出进行简单的判断从而实现预测和分类的目的，也就具有了对未知数据进行预测和分类的能力。

​ 对于开源代码，由于没有基础，很难读懂，不知道怎样去改代码从而实现自己想要的功能。在查阅许多资料和讲义后，渐渐了解了其中的意义。通过修改代码，进行一定的实验验证，得到了自己想要的答案。

​ 算法的学习过程是长远的，不能松懈。以后的工作虽不从事于该方向，但我相信通过这门课还是入门了算法方向的，这一定会从点滴中给我的工作带来帮助。
发现训练集很少时，Random Forest算法可能存在预测的准确率为0，而Adaboost不存在。但是随着训练集增加，Random Forest预测的准确率也会增加。SVM分类器与训练集的拟合时间更长，并且不易过拟合。

7.个人感想

​ 通过学习SVM，Random Forest，Adaboost三个算法，简单的了解了有监督学习算法。有监督学习将包含特征和标签信息的样本作为训练样本，通过训练样本训练得到一个最优模型，再利用这个模型将所有的输入映射为相应的输出，对输出进行简单的判断从而实现预测和分类的目的，也就具有了对未知数据进行预测和分类的能力。

​ 对于开源代码，由于没有基础，很难读懂，不知道怎样去改代码从而实现自己想要的功能。在查阅许多资料和讲义后，渐渐了解了其中的意义。通过修改代码，进行一定的实验验证，得到了自己想要的答案。

​ 算法的学习过程是长远的，不能松懈。以后的工作虽不从事于该方向，但我相信通过这门课还是入门了算法方向的，这一定会从点滴中给我的工作带来帮助。