一文搞懂二叉树的递归实现原理(图解)
一文搞懂二叉树的递归实现原理(图解)
目录
-
- 一文搞懂二叉树的递归实现原理(图解)
-
-
- 1、活动记录
- 2、举例说明
- 3、绘图说明(一定要看)
- 4、代码
-
1、活动记录
调用函数时会发生genbg什么?如果这个函数存在形参,形参就初始化为实参传递来的值。另外,函数结束后,系统要知道从哪里继续执行程序。而递归的实现就需要知道 从哪里继续执行。指示函数从何处调用的信息保存在系统中。为了做到这一点,返回地址被存储在主内存中预留的特定区域。
对于函数调用来说,需要存储的信息不只是返回地址。因此使用栈进行动态分配效果会好一些。那么调用函数时,需要保存哪些信息?
每个函数(包括主函数main())的状态由以下因素决定:函数中的所有局部变量的内容,函数参数的返回值,表明在调用函数的何处重新开始的返回地址。----包含这些信息的数据区称为活动记录或者栈框架!!!位于允许时栈。只要函数在执行,其活动记录就一下都在。活动记录一般还包括:一个指向调用程序的活动记录的指针以及非void类型的函数的返回值。

因此根据活动记录就能理解递归如何实现。递归只是被调用函数的名称正好和调用者相同。因此,递归调用不是表面上的函数调用自身,而是一个函数的实例调用同一个函数的另一个实例。
2、举例说明
(1)创建树
输入信息:[15,4,20,17,19,22] 会创建如下二叉树(二叉树按照左小右大的特点创建)
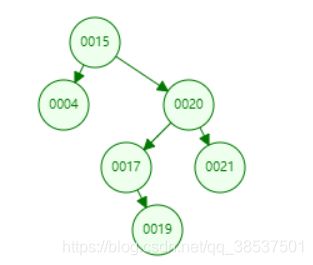
(2)以先序递归遍历进行讲解
void preorder(BSTNode* root)
{
if (root != NULL)
{
visit(root);
preorder(root->left);
preorder(root->right);//递归内部表示为活动记录
}
}
程序调用—创建活动记录
我们使用结点值表示栈中活动记录变化
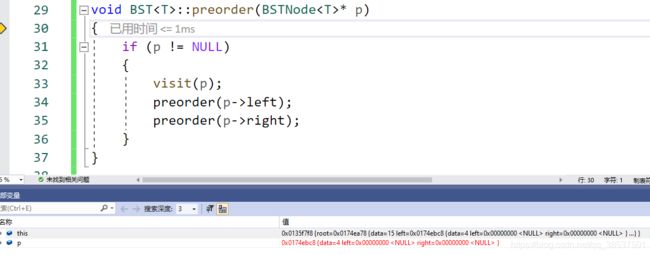
(1)15 入栈
(2)当到34行处,第一次递归调用 preorder 函数,因此会创建实例放入栈中,4入栈
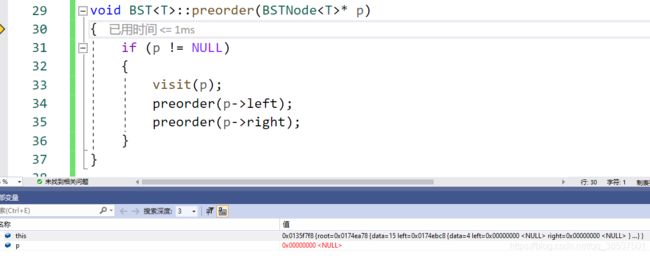
(3)继续运行,当再次运行到34行时,继续创建实例。
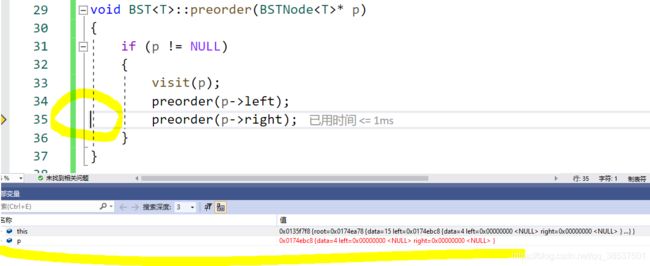
(4)但是由于p为空,那么该实例结束运行,接下来跳转到35行。
由于栈中存在15/4,那么下一个函数调用可以找到4对应的地址。然后继续向下执行,执行35行,向右子树递归寻找,然后从30行继续执行。值得注意的是假设右子树存在左子树,当运行到34行时会继续创建实例往左子树递归。
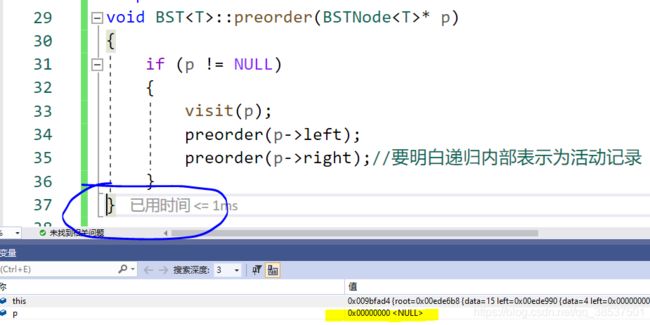
(5)由于4的右子树为空因此,程序执行到37行,**注意:**此时一轮递归才完成。那么4出栈。
(6)4出栈后,返回15的地址
(7)返回的时候会返回最近的递归(栈顶元素,栈是后入先出)。也就是调用35行,重复上述过程。难点:二叉树的递归遍历为双层套娃。当运行35行时,必然会运行到34行,也就是只有当34行一轮递归(所有活动记录出栈)完成后,才能进行35行。
3、绘图说明(一定要看)
虽然通过上面的描述可以大概理解到递归的实现,但是双重套娃(动态链接)还是无法在想象出如何实现。如下绘图展示:
说明:LS(left recursion,向左子树递归),RS(right recursion),数字表示简化的活动记录
以上就是左子树整个递归过程,然后继续往右边进行。
二叉树的递归难以理解就在于,递归函数中还存在递归。当递归结束(函数的实例结束),还需要再进行递归,所以函数的返回地址在活动记录中,就知道从哪里继续执行程序。
以上就是整个流程,如果有什么问题欢迎分享,自己最好单步运行进行理解。
4、代码
头文件:GenericBST.h
// 以下为基本二叉树需要实现的函数
//--------------generic binary search tree-----------------
#pragma once
#include
using namespace std;
template
class BSTNode{
public:
BSTNode(){
left = right = NULL;
}
BSTNode(const T& val, BSTNode* l = NULL, BSTNode* r = NULL){
data = val;
left = l;
right = r;
}
public:
T data;
BSTNode* left, * right;
};
template
class BST{
public:
BST(){
root = NULL;
}
~BST(){
root = NULL;//不能只free(root)...
}
void insertelem(const T&);
void preorder(BSTNode* root);
void inorder(BSTNode* root);
void postorder(BSTNode* root);
void breadthFirst();
void iterativePreorder();
void iterativeInorder();
void iterativePostorder();
T* search(BSTNode* root, const T& el) const;
int depth(BSTNode* root);
int getNodeNum(BSTNode* root);
int getLeafNum(BSTNode* root);
BSTNode* getroot(){
return this->root;
}
};
BSTachieve.hpp文件实现
#pragma once
#include
#include
#include"GenericBST.h"
template
T* BST::search(BSTNode* root, const T& el) const
{
BSTNode* p = root;
while (p != NULL)
{
if (p->data == el)//终止条件
return &p->data;
else if (el < p->data)
p = p->left;
else
p = p->right;
}
return NULL;//while结束,说明没找到
}
template
void BST::visit(BSTNode* p)
{
std::cout << p->data << " ";
}
template
void BST::preorder(BSTNode* p)
{
if (p != NULL)
{
visit(p);
preorder(p->left);
preorder(p->right);
}
}
template
void BST::inorder(BSTNode* root)
{
BSTNode* p = root;
if (p != NULL)
{
inorder(p->left);
visit(p);
inorder(p->right);
}
}
template
void BST::postorder(BSTNode* root)
{
BSTNode* p = root;
if (p != NULL)
{
inorder(p->left);
inorder(p->right);
visit(p);
}
}
// ------------头文件中的其他函数可以自行实现------------------
#include"GenericBST.h"
#include"BSTachieve.hpp"//含有模板需要包含实现文件 因为模板后绑定,最好写hpp。
#include "GenericBST.h"
using namespace std;
int main()
{
BST st;
for (int i = 0; i < 5; i++)
{
int val[] = { 15,4,20,17,19 };
st.insertelem(val[i]);
}
st.preorder();
return 0;
}