大疆算法笔试题目解析（二）计算机视觉

二、计算机视觉（100分）

---

1.(20分)（特征点匹配）给定两幅图像$A$和$B$，要求对两幅图中的特征点$x_i,i=1,..,m,$和$x_i^{\prime },j=1,..,n$进行匹配。特征点的结构为:{$x,y$坐标，128 位描述子}，即$x=\{intx,inty,floatdesc[128]\}$.假设两幅图中所有特征点已经找出，并按照从左到右、从上到下的扫描顺序排序;一对特征点$x_i,x_j^{\prime }$的差异由距离函数$F(x_i,x_j^{\prime })$定义，如果$F(x_i,x_{k(i)}^{\prime })\le F(x_i,x_j^{\prime }),\forall j\in [1,n],$则$x_i$与$x_{k(i)}^{\prime }$称为是一对特征点匹配对，记作$(x_i\leftrightarrow x_{k(i)}^{\prime }).$试写出特征点匹配的算法（写出伪码即可），并分析时间复杂度（不考虑函数$F$的开销）。
算法输入：按扫描顺序排序的特征点序列$x_i,i=1,...,m$和$x_j^{\prime },j=1,...,n.$
算法输出：所有特征点匹配对$(x_i\leftrightarrow x_{k(i)}^{\prime }),i=1,2,...,m.$
数据结构定义（不可更改）：

typedef struct _feature{
	int x;
	int y;
	float desc[128];
}feature;

函数声明：
C++:void featureMatch(vector x,vector xprime, vector

---

void featureMatch(vector<feature> x, vector<feature> xprime, vector<int>& k) {
    int m = x.size();
    int n = xprime.size();
    k.resize(m);

    for (int i = 0; i < m; i++) {
        int best_k = 1;  // Initialize the best match index
        float best_distance = distance(x[i], xprime[1]);

        for (int j = 2; j <= n; j++) {
            float current_distance = distance(x[i], xprime[j]);
            if (current_distance < best_distance) {
                best_k = j;
                best_distance = current_distance;
            }
        }

        k[i] = best_k;  // Store the best match index for xi
    }
}

特征点匹配的时间复杂度为 $O(m\times n)$

---

2.（20分）（图像矫正）试着设计一种算法可以将图$\text{A}$矫正成图$\text{B}$。$\text{A,B}$图的大小相同，宽高都为$w,h.$其中$\text{A}$图中的$A_1,A_2,A_3,A_4$的坐标已知，分别为$A_i=(x_i,y_i),i=1,...,4,$且对应$\text{B}$图中的四个角。并分析算法的优缺点。

---

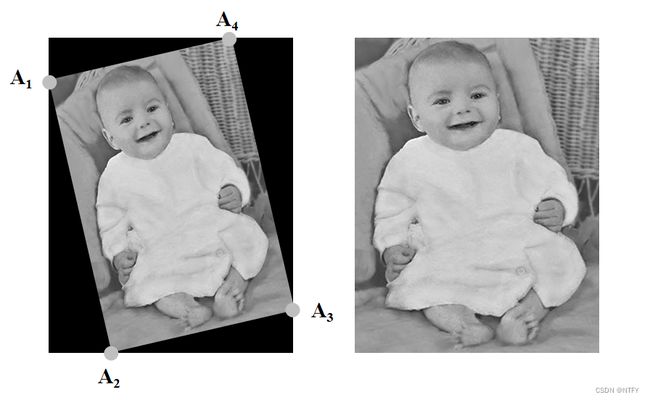
要实现图像矫正的算法，将图A矫正成图B，可以按照以下步骤进行：

1. 计算旋转角度：通过已知的点$A_1,A_2,A_3,A_4$的坐标，可以计算出图A相对于图B需要旋转的角度。可以通过计算两个向量的夹角来得到旋转角度。
2. 旋转图像：使用计算得到的旋转角度，对图A进行逆时针旋转，使其与图B的对应角点对齐。
3. 扩展图像：将旋转后的图A进行扩展，使其尺寸与图B相同。可以通过插值方法来填充新像素值，例如双线性插值。

伪代码：

function imageCorrection(imageA, A1, A2, A3, A4, imageB):
    // 计算旋转角度
    angle = calculateRotationAngle(A1, A2, A3, A4)

    // 旋转图像
    rotatedImageA = rotateImage(imageA, -angle) // 逆时针旋转

    // 扩展图像
    correctedImageA = expandImage(rotatedImageA, imageB.width, imageB.height)

    return correctedImageA

优缺点：
优点：

• 算法基于已知的四个角点坐标，不需要复杂的特征点匹配。
• 通过计算旋转角度和扩展图像，可以相对精确地将图A矫正成图B。

缺点：

• 如果角点坐标的测量存在误差，可能会导致矫正不准确。
• 对于较大的旋转角度或者图像形状较复杂的情况，可能需要额外的处理步骤来保持图像质量。
• 算法对于图像中可能存在的噪声和畸变不够鲁棒，可能需要进一步的优化和处理。

---

3.（40分）（立体视觉）考虑一个典型的立体视觉系统，如下图所示。其中$C,C^{\prime }$分别为两个相机的中心，称为光心；$e,e^{\prime }$分别为光心$C^{\prime },C$在另一个相机中的投影，称为对极点；X为三维空间中的一个点，其在两个相机的投影分别为$x,x^{\prime };$$l^{\prime }$为$e^{\prime },x^{\prime }$的连线,称为点$x$对应的极线；连线$C{C}^{\prime }$称为基线。显然，上面所提到的所有点都共面，这个平面称为极平面。
用齐次坐标表示法来表示点和线（即在真实坐标后面加上一维1，例如二维坐标系$(x,y)$的齐次坐标表示是$(x,y,1),$三维坐标$(x,y,z)$的齐次坐标表示是$(x,y,z,1)$。三维点$X$投影到图像上的二维点可以由公式$PX=x,P^{\prime }X=x^{\prime }$表示，其中$P,P^{\prime }$称为投影矩阵$(3\times 4)$。投影矩阵是不可逆的，因为所有射线$\text{CX}$上的点都投影到图像上的相同点$x$，但可以求出他的伪逆$P^{+}$，并表达出射线$\text{CX}:f(\lambda )=P^{+}x+\lambda C.$伪逆满足：$P{P}^{+}=I.$点$x$在直线$l$上可以表示为$\mathbf{x}\cdot l=x^T\mathbf{l}=0.$两点$x_1,x_2$所在的直线$l$可以由他们的叉乘表示：$l=x_1\times x_2=[x_1{]}_{\times }{x}_2,$其中$[\cdot {]}_{\times }$为反对称运算符：
[ x ] x = [ 0 − x 3 x 2 x 3 0 − x 1 − x 2 x 1 0 ] . [x]_x=\begin{bmatrix} 0 & -x_3 & x_2\\ x_3& 0& -x_1\\ -x_2&x_1&0 \end{bmatrix}. [x]x​= ​0x3​−x2​​−x3​0x1​​x2​−x1​0​ ​.

---

1)（15分）试证明点$x,x^{\prime }$满足：$x^{\prime T}Fx=0$。给出$F$的表达式，并说明它的秩是多少。
[略]
2)（25分）假设已知两幅视图中的n组匹配点对$x_i,x_i^{\prime },i=1,...,n,$试设计算法求出F.说明n最小为多少才能求得一个有效的F.
[略]

---

4.（20分）请描述你认为最重要的3个图像或视觉技术在消费类小型无人机领域的应用，并请简要说明原因以及你所能够想到的可能解决方案。

---

在消费类小型无人机领域，以下是三个重要的图像或视觉技术以及它们的应用和可能的解决方案：

1. 目标检测与跟踪：

   • 应用： 小型无人机常常需要识别和跟踪特定的目标，如人、车辆、动物等。这在监控、搜救、农业等领域有重要应用。
   • 原因： 目标检测和跟踪技术可以让无人机自动识别感兴趣的目标，并跟随它们，从而提供实时信息和数据。这种自动化可以提高效率，减轻操作员负担。
   • 解决方案： 使用深度学习的目标检测模型，如YOLO（You Only Look Once）或Faster R-CNN，可以实现实时的目标检测。通过将这些模型与无人机的视觉系统集成，可以实现目标的自动识别和跟踪。

2. 视觉导航与避障：

   • 应用： 小型无人机需要在复杂的环境中进行导航和避障，以确保安全飞行和任务完成。
   • 原因： 视觉导航和避障技术可以使无人机能够感知周围环境并作出实时决策，以避免障碍物并找到安全路径。
   • 解决方案： 使用深度学习和计算机视觉技术，无人机可以通过摄像头捕捉环境信息，并使用实时的图像处理和数据分析来实现避障。例如，结合视觉SLAM（Simultaneous Localization and Mapping）技术，可以实现无人机的定位和环境建模，从而实现更精确的导航。

3. 图像拼接与建模：

   • 应用： 小型无人机可以用于拍摄航拍照片，这在旅游、房地产、城市规划等领域有广泛应用。图像拼接技术可以将多张照片拼接成完整的全景图像，图像建模则可以生成三维模型。
   • 原因： 图像拼接和建模技术可以让无人机从不同角度捕捉到更大范围的场景，提供更全面的信息，满足不同领域的需求。
   • 解决方案： 采用图像拼接算法，如SIFT（Scale-Invariant Feature Transform）或ORB（Oriented FAST and Rotated BRIEF），可以在图像上找到关键点，并将多张照片拼接成全景图像。对于图像建模，可以使用结构光、立体视觉等方法来获得深度信息，并生成三维模型。

这三个技术在消费类小型无人机领域的应用，能够提升无人机的自主性、导航能力和数据采集效率，使其在各种领域发挥更大的作用。